湖南省永州市祁阳市2023-2024学年八年级上学期期中数学试题

试卷更新日期：2024-01-12 类型：期中考试

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分，每小题只有一个正确选项，请将正确选项填涂到答题卡的空格上）

1. 代数式 $2 x$ ， $\frac{a + b}{5}$ ， $a + \frac{x}{3}$ ， $\frac{x - 3}{x}$ ， $\frac{5 + y}{π}$ 中分式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下面各组线段中，能组成三角形的是（）

A、2，3，5 B、4，4，8 C、5，4，10 D、6，7，12

查看试题解析
3. 下列运算正确的是（）

A、 ${(a^{2})}^{3} = a^{5}$ B、 ${(- a)}^{3} \div (- a) = a^{2}$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 $a^{3} + a^{2} = a^{5}$

查看试题解析
4. 下列生活中的一些事实运用了“三角形稳定性”的是（）

A、 B、 C、 D、

查看试题解析
5. 分式 $\frac{2 x + 3 y}{3 x y}$ 中的x ， y的值都扩大到原来的10倍，则分式的值为（）

A、扩大为原来10倍 B、不变 C、缩小为原来的 $\frac{1}{10}$ 倍 D、缩小为原来的 $\frac{1}{20}$ 倍

查看试题解析
6. 如图，若 $△ A B C ≌ △ A D E$ ，点D在 $B C$ 边上，则下列结论中不一定成立的是（）

A、 $A B = A D$ B、 $A C = D E$ C、 $∠ A D B = ∠ A D E$ D、 $∠ B A D = ∠ C A E$

查看试题解析
7. 已知关于 $x$ 的分式方程 $\frac{m}{x - 2} + 1 = \frac{x}{2 - x}$ 的解是非负数，则m的取值范围是（）

A、 $m \leq 2$ B、 $m \geq 2$ C、 $m < 2$ 且 $m \neq - 2$ D、 $m \leq 2$ 且 $m \neq - 2$

查看试题解析
8. 用反证法证明“三角形的三个外角中至多有一个锐角”，应先假设（）

A、三角形的三个外角都是锐角 B、三角形的三个外角中至少有两个锐角 C、三角形的三个外角中没有锐角 D、三角形的三个外角中至少有一个锐角

查看试题解析
9. 下列关于分式的判断，正确的是（）

A、当 $x = 3$ 时， $\frac{2 x + 1}{x - 3}$ 的值为0 B、当 $x \neq 3$ 时， $\frac{x - 3}{x}$ 有意义 C、无论 $x$ 为何值， $\frac{5}{x + 1}$ 不可能是整数 D、无论 $x$ 为何值， $\frac{3}{x^{2} + 1}$ 的值总为正数

查看试题解析
10. 如图所示，在等边三角形ABC中，D ， E分别在边AB ， BC上，且 $A D = B E$ ， AE与CD交于点F ， $A G ⊥ C D$ ，垂足为点G.下列结论：① $A E = C D$ ；② $∠ A F C = 120 °$ ；③ $△ A D F$ 是等边三角形；④ $\frac{F G}{A F} = \frac{1}{2}$ ，其中正确结论的个数是（）

A、3 B、2 C、1 D、0

查看试题解析

二、填空题（本大题共6个小题，每小题3分，共18分，请将答案填在答题卡的答案栏内）

11. 人的头发发丝的直径大约为0.00007米，用科学记数法可以表示为.

查看试题解析
12. 分式 $\frac{2 x}{x - 2}$ 与 $\frac{8}{x^{2} - 2 x}$ 的最简公分母是.

查看试题解析
13. 如果等腰三角形的一个角62°，则它的底角度数为.

查看试题解析
14. 已知： $\frac{1}{x} - \frac{1}{y} = \frac{1}{4}$ ，则 $\frac{2 y + 3 x y - 2 x}{y - x - 2 x y} =$ .

查看试题解析
15. 如图， $△ A B C$ 中， $A C = 10$ ， $B C = 6$ ， AB的垂直平分线DE交AB于点D ，交边AC于点E ，则 $△ B C E$ 的周长为.

查看试题解析
16. 有一个运算程序，运算的过程如下：
则第 $n$ 次运算的结果 $y_{n} =$ .（用含有x和n的式子表示）

查看试题解析

三、解答题（本大题共9个小题，共72分，解答题要求写出证明步骤或解答过程）

17. 计算： $| - 2 | + {(\frac{1}{2})}^{- 2} - {(π - 2023)}^{0}$

查看试题解析
18. 计算： $(\frac{3 x + y}{x^{2} - y^{2}} + \frac{2 x}{y^{2} - x^{2}}) \div \frac{2}{x^{2} y - x y^{2}}$

查看试题解析
19. 已知 $x^{2} - 5 x + 1 = 0$ ，求 $2 x^{2} + \frac{2}{x^{2}}$ 的值.

查看试题解析
20. 解方程： $\frac{1}{x - 1} + 1 = \frac{3}{2 x - 2}$ ．

查看试题解析
21. 如图，在△ABC中，AB＝AC，AD⊥BC于点D．

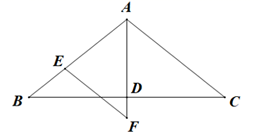(1)、若∠C＝40°，求∠BAD的度数；

(2)、若点E在边AB上，EF∥AC交AD的延长线于点F，求证：AE=FE．

查看试题解析
22. 为加快公共领域充电基础设施建设，某停车场计划购买A ， B两种型号的充电桩.已知A型充电桩比B型充电桩的单价少0.3万元，且用18万元购买A型充电桩与用24万元购买B型充电桩的数量相等.求A ， B两种型号充电桩的单价各是多少万元?

查看试题解析
23. 如图，在 $△ O A B$ 中， $∠ A O B = 90 °$ ， $O A = O B$ ，在 $△ E O F$ 中， $∠ E O F = 90 °$ ， $O E = O F$ ，连接AE ， BF.问线段AE与BF之间有什么数量关系和位置关系?请说明理由.

查看试题解析
24. a为何值时，关于x的方程 $\frac{2}{x - 2}$ + $\frac{a x}{x^{2} - 4}$ = $\frac{3}{x + 2}$ 无解？

查看试题解析
25. 如图， $△ A B C$ 中， $A B = A C = 12 c m$ ， $B C = 8 c m$ ，点D为AB的中点.如果点P在BC上以2cm/s的速度由 $B \to C$ 运动，同时，点Q在AC上以相同的速度由 $C \to A$ 运动，当点P到达点C或点Q到达点A时运动停止.

(1)、经过1s后， $△ B P D$ 与以点C ， P ， Q为顶点的三角形是否全等?为什么?

(2)、如果点Q的速度与点P（2cm/s）不等，（1）中的两个三角形是否全等?若能，求出此时点Q的速度和运动时间；若不能，请说明理由.

查看试题解析