江西省赣州市龙南区2023-2024学年八年级上学期期中数学试题
试卷更新日期:2024-01-12 类型:期中考试
一、单项选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项.)
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若一个正多边形的每一个内角的度数都是 , 则这个多边形是( )A、正九边形 B、正十边形 C、正十一边形 D、正十二边形3. 等腰三角形的顶角是 , 则一腰上的高与底边所成的角的度数是( )A、 B、 C、 D、4. 如图, , 添加一个条件,不能判断的是( )
2. 若一个正多边形的每一个内角的度数都是 , 则这个多边形是( )A、正九边形 B、正十边形 C、正十一边形 D、正十二边形3. 等腰三角形的顶角是 , 则一腰上的高与底边所成的角的度数是( )A、 B、 C、 D、4. 如图, , 添加一个条件,不能判断的是( )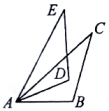 A、 B、 C、 D、5. 如图,点在的垂直平分线上,若 , 则为( )
A、 B、 C、 D、5. 如图,点在的垂直平分线上,若 , 则为( )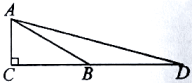 A、4 B、6 C、8 D、106. 如图,在的方格纸中有一个以格点为顶点的 , 则与成轴对称且以格点为顶点的三角形共有( )个.
A、4 B、6 C、8 D、106. 如图,在的方格纸中有一个以格点为顶点的 , 则与成轴对称且以格点为顶点的三角形共有( )个.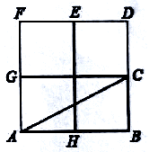 A、3个 B、4个 C、5个 D、6个
A、3个 B、4个 C、5个 D、6个二、填空题(本大题共6小题,每小题3分,共18分.)
-
7. 已知点关于轴对称的对称点的坐标是.8. 一个多边形的每个外角的度数都是 , 则这个多边形边数为.9. 一副三角板,如图所示叠放在一起,则图中的度数为.
 10. 如图,把一张长方形纸片沿折叠后与的交点为 , 分别在、的位置上,若 , 则.
10. 如图,把一张长方形纸片沿折叠后与的交点为 , 分别在、的位置上,若 , 则.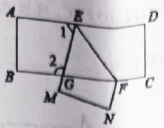 11. 已知等腰的两边长分别为2和5,则等腰的周长为.12. 如图所示,在等腰中,为的中点,点在上, , 若点是等腰的腰上的一点,则当为等腰三角形时,的度数是.
11. 已知等腰的两边长分别为2和5,则等腰的周长为.12. 如图所示,在等腰中,为的中点,点在上, , 若点是等腰的腰上的一点,则当为等腰三角形时,的度数是.
三、(本大题共5小题,每小题6分,共30分.)
-
13. 在中,是边上的一点,.
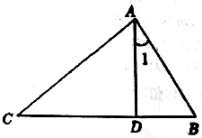
求证:
(1)、.(2)、14. 如图,为上一点,.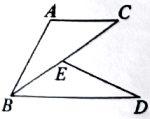
求证:.
15. 如果一个三角形的一边长为 , 另一边长为;若第三边长为.(1)、第三边的范围为.(2)、当第三边长为奇数时,求出这个三角形的周长,并指出它是什么三角形(按边分类).16. 如图所示,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.的顶点均在格点上,点的坐标分别是 , 关于轴对称的图形为. (1)、画出;(2)、求出的面积;(3)、在轴上找出一点 , 使的值最小.(不写画法,但需保留作图痕迹)17. 小明在学习完“等腰三角形底边上的高线、中线及顶角平分线重合”,继续探索,他猜想“如果三角形的一条角平分线是这个角对边上的中线,那么这个三角形是等腰三角形”并进行了证明.(1)、请根据以上命题和图形写出已知和求证:
(1)、画出;(2)、求出的面积;(3)、在轴上找出一点 , 使的值最小.(不写画法,但需保留作图痕迹)17. 小明在学习完“等腰三角形底边上的高线、中线及顶角平分线重合”,继续探索,他猜想“如果三角形的一条角平分线是这个角对边上的中线,那么这个三角形是等腰三角形”并进行了证明.(1)、请根据以上命题和图形写出已知和求证:已知: ▲ ,
求证: ▲ .
(2)、请证明以上命题.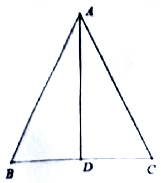
四、(本大题3小题,每小题8分,共24分.)
-
18. 在中,上的中线把三角形的周长分为和两个部分,求的三边长.
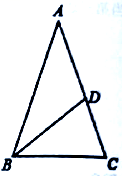 19. 如图,在等边三角形中,点三点在同一条直线上,且 , .判断是什么形状,并说明理由.
19. 如图,在等边三角形中,点三点在同一条直线上,且 , .判断是什么形状,并说明理由.
 20. 已知:如图, , 垂足分别为.
20. 已知:如图, , 垂足分别为. (1)、线段和的数量关系是;(2)、请写出线段之间的数量关系并证明.
(1)、线段和的数量关系是;(2)、请写出线段之间的数量关系并证明.五、(本大题共2小题,每小题9分,共18分.)
-
21. 如图,在中, , 过点作线段 , 连接 , 且满足.取的中点 , 连接.
 (1)、若 , 直接写出的取值范围;(2)、求证:.22. 如图,在中, , 动点以的速度从点向点运动,动点以的速度从点向点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为.
(1)、若 , 直接写出的取值范围;(2)、求证:.22. 如图,在中, , 动点以的速度从点向点运动,动点以的速度从点向点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为. (1)、求证:;(2)、当取何值时,与全等.
(1)、求证:;(2)、当取何值时,与全等.六、(本大题共12分.)
-
23. 在中, , 点是直线上一点(不与重合),以为一边在的右侧作 , 传 , 连接.
图1
 图2
图2 备用图
备用图 备用图
备用图 (1)、如图1,当点在线段上,如果 , 则度;(2)、设.
(1)、如图1,当点在线段上,如果 , 则度;(2)、设.①如图2,当点在线段上移动,则之间有怎样的数量关系?请说明理由;
②当点在直线上移动,则之间有怎样的数量关系?请直接写出你的结论.