江西省九江市都昌县2023-2024学年九年级上学期期中数学试题
试卷更新日期:2024-01-12 类型:期中考试
一、选择题(每小题3分,共18分)
-
1. 下列说法错误的是( )A、平行四边形的对边相等 B、正方形的对角线互相垂直平分且相等 C、菱形的对角线相等且平分 D、矩形的对角线相等且互相平分2. 关于x的一元二次方程的常数项为0,则m的值为( )A、3 B、0 C、3或0 D、23. 某轨道列车共有3节车厢,设旅客从任意一节车厢上车的机会均等,某天,甲、乙两位乘客同时乘一列轨道列车,则甲和乙从同一节车厢上车的概率是( )A、 B、 C、 D、4. 如图,已知下列条件不能判定的是( )
 A、 B、 C、 D、5. 小华仿照探究一元二次方程解的方法,课后尝试探究了一元三次方程的解,列表如下:
A、 B、 C、 D、5. 小华仿照探究一元二次方程解的方法,课后尝试探究了一元三次方程的解,列表如下:x
0
0.5
1
1.5
2
-1
-5.375
-3
6.875
25
据此可知,方程的一个解x的取值范围是( )
A、 B、 C、 D、6. 如图,为正方形对角线的中点,为等边三角形.若 , 则的长度为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题共6小题,每小题3分,共18分)
-
7. 如图,在菱形ABCD中, , 则.
 8. 关于x的一元二次方程有实数根,则a的取值范围是 .9. 在一个不透明的袋子里装有红球和白球30个,这些球除颜色外都相同,小明通过多次试验发现,摸出白球的频率稳定在0.3左右,则袋子里可能有个白球.10. 若a , b是方程的两个实数根,则的值为.11. 如图,点P是正方形ABCD内位于对角线AC下方的一点,若 , 则的度数为.
8. 关于x的一元二次方程有实数根,则a的取值范围是 .9. 在一个不透明的袋子里装有红球和白球30个,这些球除颜色外都相同,小明通过多次试验发现,摸出白球的频率稳定在0.3左右,则袋子里可能有个白球.10. 若a , b是方程的两个实数根,则的值为.11. 如图,点P是正方形ABCD内位于对角线AC下方的一点,若 , 则的度数为. 12. 如图, , , , , , 点P在BD上,由点B向点D方向移动,当与相似时,BP的长为.
12. 如图, , , , , , 点P在BD上,由点B向点D方向移动,当与相似时,BP的长为.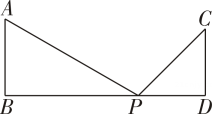
三、解答题(本题共5小题,每小题6分,共30分)
-
13.(1)、解方程:.(2)、如图:在正方形ABCD中,点E、F在AC上,且 , 求证:四边形BEDF是菱形.
 14. 先阅读下面某校九年级师生的对话内容,再解答问题(温馨提示:一周只上五天课,另外,考试时每半天考一科且只能安排在周一到周五)
14. 先阅读下面某校九年级师生的对话内容,再解答问题(温馨提示:一周只上五天课,另外,考试时每半天考一科且只能安排在周一到周五)小红:“听说下周会进行连续两天的期中考试.”
吴老师:“是的,要考语文、数学、英语、物理共四科,但具体星期几不清楚.”
小凡:“我估计是星期四、星期五.”
(1)、求小凡猜对的概率.(2)、若考试已定在星期四、星期五进行,但各科考试顺序没定,请用列表或画树状图的方式求恰好在同一天考语文、数学的概率.15. 如图,已知 , , 求证:. 16. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽,每株脚钱三文足,无钱准与一株椽”,其大意为:现请人代买一批椽,这批椽的价钱为6210文,如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价格,求这批椽的数量有多少株?17. 如图,在正方形ABCD中, , 请仅用无刻度的直尺画图(保留画图痕迹,不写画法).
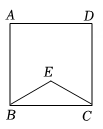
16. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽,每株脚钱三文足,无钱准与一株椽”,其大意为:现请人代买一批椽,这批椽的价钱为6210文,如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价格,求这批椽的数量有多少株?17. 如图,在正方形ABCD中, , 请仅用无刻度的直尺画图(保留画图痕迹,不写画法).图①
 图②
图②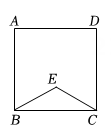 (1)、在图①中,画出AD的中点M;(2)、在图②中,画出CD的中点N.
(1)、在图①中,画出AD的中点M;(2)、在图②中,画出CD的中点N.四、(本大题共3小题,每小题8分,共24分)
-
18. 如图,一张矩形纸片ABCD , 将点B折叠到对角线AC上的一点M处,折痕CE交AB于点E , 将点D折叠到对角线AC上的点H处,折痕AF交DC于点F.
 (1)、求证:.(2)、当的大小为多少度时,四边形AECF是菱形?请说明理由.19. 已知关于x的方程.(1)、求证:无论k取任何实数,该方程都有两个不相等的实数根;(2)、当该方程的一个根为1时,求k的值及该方程的另一个根.20. 如图,在和中,已知 , , , , , 连接AD、BE.
(1)、求证:.(2)、当的大小为多少度时,四边形AECF是菱形?请说明理由.19. 已知关于x的方程.(1)、求证:无论k取任何实数,该方程都有两个不相等的实数根;(2)、当该方程的一个根为1时,求k的值及该方程的另一个根.20. 如图,在和中,已知 , , , , , 连接AD、BE. (1)、求证:.(2)、若 , 求的面积.
(1)、求证:.(2)、若 , 求的面积.五、(本大题共2小题,每小题9分,共18分)
-
21. 电影(长津湖)是一部讲述抗美援朝题材的影片,该片以朝鲜长津湖战役为背景,讲述一个志愿军连队在极严寒环境下坚守阵地奋勇杀敌,为战役胜利作出重要贡献的故事,2023年国庆节来临之际,某电影院开展“纪念英烈,铸中华魂”系列活动,对团体购买电影票实际优惠,决定在原定零售票价基础上每张降价16元,这样按原定零售票价需花费2000元购买的门票,现在只需花1200元.(1)、求每张电影票的原定零售票价?(2)、为了弘扬爱国主义精神,该影院决定对网上购票的个人也采取优惠,原定零售票价经过连续两次降价后票价为每张32.4元,求平均每次降价的百分率.22. 如图①,在中, , , 点D、E分别是边BC、AC的中点,连接DE , 将绕点C按顺时针方向旋转,记旋转角为.

备用图
(1)、问题发现:①当时,.
②当时,.
(2)、拓展探究:当时,的大小有无变化?仅就图②的情形给出证明;
(3)、问题解决:当旋转至A、D、E三点共线时,直接写出线段BD的长.
六、解答题
-
23. 如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
 (1)、求证:.(2)、连接MQ、PN , 判断四边形MPNQ的形状,并说明理由.(3)、矩形ABCD的边AB与AD满足什么长度关系时,四边形MPNQ是正方形?请说明理由.
(1)、求证:.(2)、连接MQ、PN , 判断四边形MPNQ的形状,并说明理由.(3)、矩形ABCD的边AB与AD满足什么长度关系时,四边形MPNQ是正方形?请说明理由.