湖南省邵阳市2023-2024学年九年级上学期数学月考考试试卷
试卷更新日期:2024-01-12 类型:月考试卷
一、选择题(本大题共10个小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的;请将你认为正确的选项填涂到答题卡上)
-
1. 的相反数是( )A、 B、 C、 D、2. 下面四个化学仪器示意图中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2023年10月26日神舟十七号载人飞船发射取得圆满成功,我国载人航天工程发射任务实现30战30捷,航天员在中国空间站俯瞰地球的高度约为400000米,将400000用科学记数法表示应为( )A、 B、 C、 D、4. 下列运算结果正确的是( )A、 B、 C、 D、5. 若代数式 在实数范围内有意义,则 的取值范围是A、x<1 B、x≤1 C、x>1 D、x≥16. 光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,的度数为( )
3. 2023年10月26日神舟十七号载人飞船发射取得圆满成功,我国载人航天工程发射任务实现30战30捷,航天员在中国空间站俯瞰地球的高度约为400000米,将400000用科学记数法表示应为( )A、 B、 C、 D、4. 下列运算结果正确的是( )A、 B、 C、 D、5. 若代数式 在实数范围内有意义,则 的取值范围是A、x<1 B、x≤1 C、x>1 D、x≥16. 光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,的度数为( )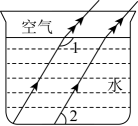 A、 B、 C、 D、7. 在一次中学生田径运动会上,参加男子跳高的10名运动员的成绩如下表所示:
A、 B、 C、 D、7. 在一次中学生田径运动会上,参加男子跳高的10名运动员的成绩如下表所示:成绩/m
1.40
1.50
1.60
1.70
1.80
人数/名
1
3
2
3
1
则这10名运动员成绩的中位数是( )
A、 B、 C、 D、8. 已知:将直线y=x﹣1向上平移2个单位长度后得到直线y=kx+b,则下列关于直线y=kx+b的说法正确的是( )
A、经过第一、二、四象限 B、与x轴交于(1,0) C、与y轴交于(0,1) D、y随x的增大而减小9. 某班学生去距学校的博物馆参观,一部分学生骑自行车先走,过了后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,设骑车学生的速度为 , 下列方程正确的是( )A、 B、 C、 D、10. 如图,点A在曲线到上,点B在双曲线上,轴,点C是x轴上一点,连接、 , 若的面积是6,则k的值( )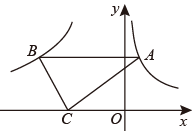 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8个小题,每小题3分,共24分;请将答案填在答题卡的答案栏内)
-
11. 9的算术平方根是 .12. 分解因式:13. 在平面直角坐标系中,若点与点关于原点对称,则的值是 .14. 已知关于x的一元二次方程的两个实数根分别为和 , 则的值为 .15. 若菱形的两条对角线长分别为6和8,则该菱形的面积为 .16. 如图,在 中,分别以点 和点 为圆心,大于 的长为半径作圆弧,两弧相交于点 和点 ,作直线 交 于点 ,连接 .若 , ,则 的周长为.
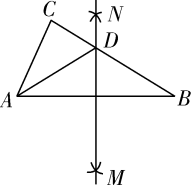 17. 如图,点在同一水平线上,和均为直角,与相交于点 . 测得 , 则树高m.
17. 如图,点在同一水平线上,和均为直角,与相交于点 . 测得 , 则树高m. 18. 如图,已知 , 点在线段上,是底边长为6的等腰三角形且 , 以为边在的右侧作矩形 , 连接 , 点是的中点,连接 , 则线段的最小值为 .
18. 如图,已知 , 点在线段上,是底边长为6的等腰三角形且 , 以为边在的右侧作矩形 , 连接 , 点是的中点,连接 , 则线段的最小值为 .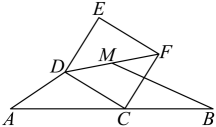
三、解答题(本大题共8个小题,第19-25题每题8分,第26题10分,共66分,解答应写出必要的文字说明、演算步骤或证明过程)
-
19. 计算: .20. 先化简,再求值: , 其中 .21. 在中,是斜边上的高.
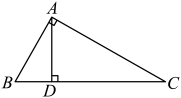 (1)、证明:;(2)、若 , 求的长.22. 今年是毛泽东等老一辈革命家为雷锋同志题词60周年,为深入贯彻落实党的二十大精神,大力弘扬宣传雷锋精神,某学校举行了以“传承雷锋精神,争当追锋少年”为主题的知识竞赛活动,竞赛满分为10分,学生成绩平均在7分以上,将成绩10分、9分、8分、7分,分别定为A,B,C,D四个等级.学校随机抽取部分学生的竞赛成绩绘制统计图,请回答下列问题:
(1)、证明:;(2)、若 , 求的长.22. 今年是毛泽东等老一辈革命家为雷锋同志题词60周年,为深入贯彻落实党的二十大精神,大力弘扬宣传雷锋精神,某学校举行了以“传承雷锋精神,争当追锋少年”为主题的知识竞赛活动,竞赛满分为10分,学生成绩平均在7分以上,将成绩10分、9分、8分、7分,分别定为A,B,C,D四个等级.学校随机抽取部分学生的竞赛成绩绘制统计图,请回答下列问题: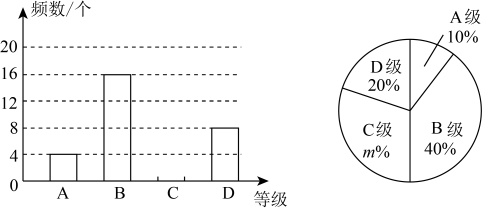 (1)、学校随机抽取的学生人数为;(2)、补全条形统计图;(3)、在扇形统计图中,“C”部分所对应的圆心角的度数为度;(4)、如果该校共有学生人,且规定等级为A、B的为优秀,请估计该校学生在此次知识竞赛活动中成绩为优秀的有多少人?23. 如图,矩形中,过对角线的中点作的垂线 , 分别交 , 于点 , , 连接、.
(1)、学校随机抽取的学生人数为;(2)、补全条形统计图;(3)、在扇形统计图中,“C”部分所对应的圆心角的度数为度;(4)、如果该校共有学生人,且规定等级为A、B的为优秀,请估计该校学生在此次知识竞赛活动中成绩为优秀的有多少人?23. 如图,矩形中,过对角线的中点作的垂线 , 分别交 , 于点 , , 连接、.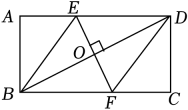 (1)、求证:≌;(2)、若求四边形的周长.24. “健康湖南,云动潇湘”,为迎接2023年全民健身线上运动会,某中学计划购进一批篮球和排球.若购买3个篮球和1个排球共需360元;若购买5个篮球和3个排球共需680元.(1)、求每个篮球和每个排球的价格分别是多少元?(2)、该学校计划购进篮球和排球共100个,且购买篮球的个数不少于排球个数的3倍,怎样购买才能使总费用最少?并求出最少总费用.25. 随着科技的发展,无人机已广泛应用于生产生活,如代替人们在高空测量距离和高度.圆圆要测量教学楼的高度,借助无人机设计了如下测量方案:如图,圆圆在离教学楼底部米的C处,遥控无人机旋停在点C的正上方的点D处,测得教学楼的顶部B处的俯角为 , 长为米.已知目高为米.
(1)、求证:≌;(2)、若求四边形的周长.24. “健康湖南,云动潇湘”,为迎接2023年全民健身线上运动会,某中学计划购进一批篮球和排球.若购买3个篮球和1个排球共需360元;若购买5个篮球和3个排球共需680元.(1)、求每个篮球和每个排球的价格分别是多少元?(2)、该学校计划购进篮球和排球共100个,且购买篮球的个数不少于排球个数的3倍,怎样购买才能使总费用最少?并求出最少总费用.25. 随着科技的发展,无人机已广泛应用于生产生活,如代替人们在高空测量距离和高度.圆圆要测量教学楼的高度,借助无人机设计了如下测量方案:如图,圆圆在离教学楼底部米的C处,遥控无人机旋停在点C的正上方的点D处,测得教学楼的顶部B处的俯角为 , 长为米.已知目高为米. (1)、求教学楼的高度.(2)、若无人机保持现有高度沿平行于的方向,以米/秒的速度继续向前匀速飞行,求经过多少秒时,无人机刚好离开圆圆的视线 .26. 如图,直线与轴交于点 , 与轴交于点 . 是一元二次方程的一个根,且 , 点为的中点,为轴正半轴上一点, , 直线与相交于点 .
(1)、求教学楼的高度.(2)、若无人机保持现有高度沿平行于的方向,以米/秒的速度继续向前匀速飞行,求经过多少秒时,无人机刚好离开圆圆的视线 .26. 如图,直线与轴交于点 , 与轴交于点 . 是一元二次方程的一个根,且 , 点为的中点,为轴正半轴上一点, , 直线与相交于点 .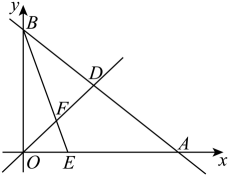 (1)、求点及点的坐标;(2)、反比例函数经过点关于轴的对称点 , 求的值;(3)、在直线上是否存在点 , 使为等腰三角形?若存在,直接写出点的坐标;若不存在,请说明理由.
(1)、求点及点的坐标;(2)、反比例函数经过点关于轴的对称点 , 求的值;(3)、在直线上是否存在点 , 使为等腰三角形?若存在,直接写出点的坐标;若不存在,请说明理由.