江西省新余市2023-2024学年八年级上学期数学第二次月考考试试卷
试卷更新日期:2024-01-12 类型:月考试卷
一、单选题(每小题3分,共18分)
-
1. 下列图案中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 在和中, , , 若证 , 还要从下列条件中补选一个,错误的选法是( )A、 B、 C、 D、4. 若 中不含x的一次项,则m的值为(A、8 B、 C、0 D、8或5. 如图,长方形ABCD为一长条形纸带, , 将ABCD沿EF折叠,C , D两点分别与对应,若 , 则的度数为( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 在和中, , , 若证 , 还要从下列条件中补选一个,错误的选法是( )A、 B、 C、 D、4. 若 中不含x的一次项,则m的值为(A、8 B、 C、0 D、8或5. 如图,长方形ABCD为一长条形纸带, , 将ABCD沿EF折叠,C , D两点分别与对应,若 , 则的度数为( )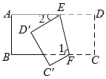 A、 B、 C、 D、6. 一个正方形和两个等边三角形的位置如图所示.若 , 则( )
A、 B、 C、 D、6. 一个正方形和两个等边三角形的位置如图所示.若 , 则( )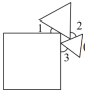 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共18分)
-
7. 在直角坐标系中,点和点关于y轴对称,则m的值为 .8. 已知是完全平方式,则 .9. 用一条长为20cm的细绳围成一个等腰三角形,使其一边长是另一边长的2倍,则此等腰三角形的一腰长为 .10. 如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,AE=7cm,AP=4cm,则P点到直线AB的距离是 .
 11. 若 , 则的值为 .12. 如图,点P、Q分别是边长为4cm的等边边AB、BC上的动点,点P从顶点A , 点Q从顶点B同时出发,且速度都为1cm/s,连接AQ、CP交于点M , 下面四个结论:①;②;③的度数不变,始终等于;④当第秒或第秒时,为直角三角形,正确的结论有 .
11. 若 , 则的值为 .12. 如图,点P、Q分别是边长为4cm的等边边AB、BC上的动点,点P从顶点A , 点Q从顶点B同时出发,且速度都为1cm/s,连接AQ、CP交于点M , 下面四个结论:①;②;③的度数不变,始终等于;④当第秒或第秒时,为直角三角形,正确的结论有 .
三、解答题(每小题6分,共30分)
-
13. 计算:(1)、(2)、14. 先化简,再求值:
, 其中 , .
15. 如图,在中,已知 , 于点D .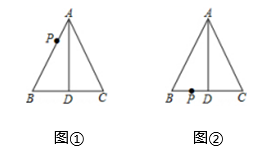 (1)、如图①,点P为AB上任意一点,请你用无刻度的直尺在AC上找出一点 , 使 .(2)、如图②,点P为BD上任意一点,请你用无刻度的直尺在CD上找出一点 , 使 .16. 一个正多边形的一个内角减去与它相邻的一个外角的结果为 . 求这个多边形的边数和内角和度数.17. 如图, 于 , 于 ,若 , .求证: 平分 .
(1)、如图①,点P为AB上任意一点,请你用无刻度的直尺在AC上找出一点 , 使 .(2)、如图②,点P为BD上任意一点,请你用无刻度的直尺在CD上找出一点 , 使 .16. 一个正多边形的一个内角减去与它相邻的一个外角的结果为 . 求这个多边形的边数和内角和度数.17. 如图, 于 , 于 ,若 , .求证: 平分 .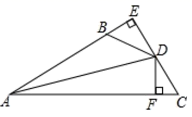
四、解答题(每小题8分,共24分)
-
18. 如图,三个顶点的坐标分别为 , ,
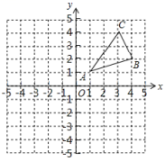 (1)、请画出将关于y轴对称后的图形;(2)、请求出的面积;(3)、在x轴上找一点P , 使的值最小,作图并根据图像直接写出点P的坐标.19. 如图,在中, , 过点B作于点D , BE平分交AC于点E .
(1)、请画出将关于y轴对称后的图形;(2)、请求出的面积;(3)、在x轴上找一点P , 使的值最小,作图并根据图像直接写出点P的坐标.19. 如图,在中, , 过点B作于点D , BE平分交AC于点E .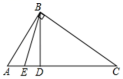 (1)、求证:;(2)、若 , 求的度数.20. 已知,如图①,在和中, , ,
(1)、求证:;(2)、若 , 求的度数.20. 已知,如图①,在和中, , ,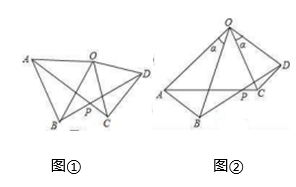 (1)、求证:①;②;(2)、如图②,在和中, , , , 则AC与BD的等量关系为 . 的大小为 . (直接写出结果,不需要证明)
(1)、求证:①;②;(2)、如图②,在和中, , , , 则AC与BD的等量关系为 . 的大小为 . (直接写出结果,不需要证明)五、解答题(每小题9分,共18分)
-
21. 如图,在中, , 点D在内, , , 点E在外, , .
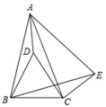 (1)、求的度数.(2)、判断的形状并说明.(3)、连接DE , 若 , , 求AD的长22. 阅读材料题:
(1)、求的度数.(2)、判断的形状并说明.(3)、连接DE , 若 , , 求AD的长22. 阅读材料题:我们知道 , 所以代数式的最小值为0.学习了多项式乘法中的完全平方公式,可以逆用公式,即用来求一些多项式的最小值.
例如,求的最小值问题.
解:∵ ,
又∵ ,
∴ ,
∴的最小值为 .
请应用上述思想方法,解决下列问题:
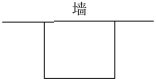 (1)、探究:()2+;(2)、代数式有最(填“大”或“小”)值为;(3)、如图,矩形花圃一面靠墙(墙足够长),另外三面所围成的提栏的总长是40m,楼栏如何围能使花圃米面积最大?最大面积是多少?
(1)、探究:()2+;(2)、代数式有最(填“大”或“小”)值为;(3)、如图,矩形花圃一面靠墙(墙足够长),另外三面所围成的提栏的总长是40m,楼栏如何围能使花圃米面积最大?最大面积是多少?六、(本大题共12分)
-
23. 如图1,点A和点B分别在y轴正半轴和x轴负半轴上,且 , 点C和点D分别在第四象限和第一象限,且 , , 点D的坐标为 , 且满足 .
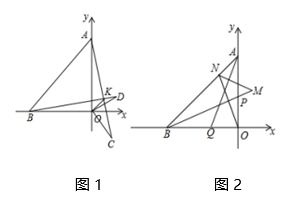 (1)、求点D的坐标;(2)、求的度数;(3)、如图2,点P , Q分别在y轴正半轴和x轴负半轴上,且 , 直线交AB于点N , 交BP的延长线于点M , 判断ON , MN , BM的数量关系并说明.
(1)、求点D的坐标;(2)、求的度数;(3)、如图2,点P , Q分别在y轴正半轴和x轴负半轴上,且 , 直线交AB于点N , 交BP的延长线于点M , 判断ON , MN , BM的数量关系并说明.