山东省青岛市西海岸新区2023-2024学年九年级上学期12月月考数学检测试题
试卷更新日期:2024-01-12 类型:月考试卷
一、选择题(每题3分,共30分)
-
1. 如图所示几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列函数中,是二次函数的有( )
2. 下列函数中,是二次函数的有( )① , ② , ③ , ④
A、个 B、个 C、个 D、个3. 小红上学要经过两个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的机会是( )A、 B、 C、 D、4. 已知反比例函数的图象在第二、四象限内,则m的值是( )A、2 B、 C、 D、05. 如图,在中,点分别是的中点,则下列结论不正确的是( ) A、 B、 C、 D、6. 如图,在平面直角坐标系xOy中,以原点O为位似中心,把线段AB放大后得到线段CD.若点A(1,2),B(2,0),D(5,0),则点A的对应点C的坐标是( )
A、 B、 C、 D、6. 如图,在平面直角坐标系xOy中,以原点O为位似中心,把线段AB放大后得到线段CD.若点A(1,2),B(2,0),D(5,0),则点A的对应点C的坐标是( )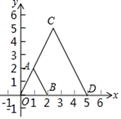 A、(2,5) B、( ,5) C、(3,5) D、(3,6)7. 已知抛物线y= 上有三点A(﹣2, ),B(﹣1,),C(2,),则 , , 的大小关系为( )A、 B、 C、 D、8. 关于二次函数 ,下列说法正确的是( )A、图像与 轴的交点坐标为 B、图像的对称轴在 轴的右侧 C、当 时, 的值随 值的增大而减小 D、 的最小值为-39. 在同一直角坐标系中,反比例函数y= 与一次函数y=ax+b的图象可能是( )A、
A、(2,5) B、( ,5) C、(3,5) D、(3,6)7. 已知抛物线y= 上有三点A(﹣2, ),B(﹣1,),C(2,),则 , , 的大小关系为( )A、 B、 C、 D、8. 关于二次函数 ,下列说法正确的是( )A、图像与 轴的交点坐标为 B、图像的对称轴在 轴的右侧 C、当 时, 的值随 值的增大而减小 D、 的最小值为-39. 在同一直角坐标系中,反比例函数y= 与一次函数y=ax+b的图象可能是( )A、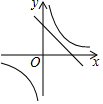 B、
B、 C、
C、 D、
D、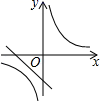 10. 勾股定理的证明方法丰富多样,其中我国古代数学家赵爽利用“弦图”的证明简明、直观,是世界公认最巧妙的方法.“赵爽弦图”已成为我国古代数学成就的一个重要标志,千百年来倍受人们的喜爱.小亮在如图所示的“赵爽弦图”中,连接 , . 若正方形与的边长之比为 , 则等于( )
10. 勾股定理的证明方法丰富多样,其中我国古代数学家赵爽利用“弦图”的证明简明、直观,是世界公认最巧妙的方法.“赵爽弦图”已成为我国古代数学成就的一个重要标志,千百年来倍受人们的喜爱.小亮在如图所示的“赵爽弦图”中,连接 , . 若正方形与的边长之比为 , 则等于( )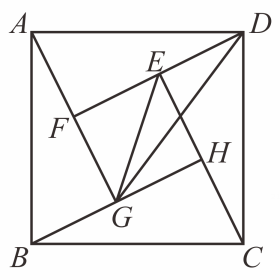 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 在Rt中, , , 则 .12. 抛物线 的顶点坐标为 .13. 如图,在平面直角坐标系中,点A是x轴上任意一点,轴,分别交 , 的图象于B , C两点,若的面积是3,则k的值为;
 14. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为.
14. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为.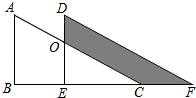 15. 如图,在边长1正网格中,A、B、C都在格点上,AB与CD相交于点D , 则sin ∠ADC= .
15. 如图,在边长1正网格中,A、B、C都在格点上,AB与CD相交于点D , 则sin ∠ADC= . 16. 如图,在中, , 分别以和为边向外作正方形和正方形 , 过点作的延长线的垂线,垂足为点 . 连接 , 交的延长线于点 . 下列说法:①;②若 , , 则;③;④;⑤若 , , 则的面积为 , 正确的有 . (填序号)
16. 如图,在中, , 分别以和为边向外作正方形和正方形 , 过点作的延长线的垂线,垂足为点 . 连接 , 交的延长线于点 . 下列说法:①;②若 , , 则;③;④;⑤若 , , 则的面积为 , 正确的有 . (填序号)
三、计算题(每题4分,共16分)
-
17.(1)、 .(2)、关于x的一元二次方程有两个相等的实数根.
(ⅰ)求m的值;
(ⅱ)求此方程的根.
(3)、写出下列抛物线的开口方向、对称轴和顶点坐标:(i);
(ii) .
18. 在平整的地面上,有若干个完全相同的棱长为的小正方体堆成一个几何体,如图所示: (1)、请画出这个几何体从正面、左面、上面看到的几何体的形状图;(2)、如果在这个几何体露在外面的表面喷上黄色的漆,每平方厘米用2克,则共需克漆;(3)、若现在你手头还有一些相同的小正方体,如果保持从上面看和从左边看不变,最多可以再添加个小正方体.19. 为践行青岛市中小学生“十个一”行动,某校举行文艺表演,小静和小丽想合唱一首歌.小静想唱《红旗飘飘》,而小丽想唱《大海啊,故乡》.她们想通过做游戏的方式来决定合唱哪一首歌,于是一起设计了一个游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.同时转动两个转盘,若两个指针指向的数字之积小于4,则合唱《大海啊,故乡》,否则合唱《红旗飘飘》;若指针刚好落在分割线上,则需要重新转动转盘.请用列表或画树状图的方法说明这个游戏是否公平.
(1)、请画出这个几何体从正面、左面、上面看到的几何体的形状图;(2)、如果在这个几何体露在外面的表面喷上黄色的漆,每平方厘米用2克,则共需克漆;(3)、若现在你手头还有一些相同的小正方体,如果保持从上面看和从左边看不变,最多可以再添加个小正方体.19. 为践行青岛市中小学生“十个一”行动,某校举行文艺表演,小静和小丽想合唱一首歌.小静想唱《红旗飘飘》,而小丽想唱《大海啊,故乡》.她们想通过做游戏的方式来决定合唱哪一首歌,于是一起设计了一个游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.同时转动两个转盘,若两个指针指向的数字之积小于4,则合唱《大海啊,故乡》,否则合唱《红旗飘飘》;若指针刚好落在分割线上,则需要重新转动转盘.请用列表或画树状图的方法说明这个游戏是否公平. 20. 如图,直线与双曲线相交于点 , .
20. 如图,直线与双曲线相交于点 , .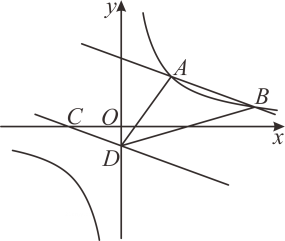 (1)、求双曲线及直线对应的函数表达式;(2)、将直线向下平移至处,其中点 , 点在轴上.连接 , , 求的面积;(3)、请直接写出关于的不等式的解集.21. 如图,在平行四边形ABCD中,点E , F , G , H分别在边AB , BC , CD , DA上,AE=CG , AH=CF , 且EG平分∠HEF .
(1)、求双曲线及直线对应的函数表达式;(2)、将直线向下平移至处,其中点 , 点在轴上.连接 , , 求的面积;(3)、请直接写出关于的不等式的解集.21. 如图,在平行四边形ABCD中,点E , F , G , H分别在边AB , BC , CD , DA上,AE=CG , AH=CF , 且EG平分∠HEF .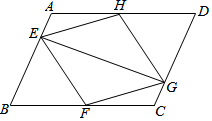 (1)、求证:△AEH≌△CGF .(2)、若∠EFG=90°.求证:四边形EFGH是正方形.22. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线,为了测量房屋的高度,在地面上C点测得屋顶A的仰角为 , 此时地面上C点、屋檐上E点、屋顶上A点三点恰好共线,继续向房屋方向走到达点D时,又测得屋檐E点的仰角为 , 房屋的顶层横梁 , , 交于点G(点C , D , B在同一水平线上).(参考数据: , , , , , )
(1)、求证:△AEH≌△CGF .(2)、若∠EFG=90°.求证:四边形EFGH是正方形.22. 脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高所在的直线,为了测量房屋的高度,在地面上C点测得屋顶A的仰角为 , 此时地面上C点、屋檐上E点、屋顶上A点三点恰好共线,继续向房屋方向走到达点D时,又测得屋檐E点的仰角为 , 房屋的顶层横梁 , , 交于点G(点C , D , B在同一水平线上).(参考数据: , , , , , ) (1)、求屋顶到横梁的距离;(2)、求房屋的高(结果精确到).23. 某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.(1)、填表(不需化简)
(1)、求屋顶到横梁的距离;(2)、求房屋的高(结果精确到).23. 某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.(1)、填表(不需化简)入住的房间数量
房间价格
总维护费用
提价前
60
200
60×20
提价后
(2)、若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)24. 如图,个边长为2的等边三角形有一条边在同一直线上,设的面积为 , 的面积为 , 的面积为 . (1)、【规律探究】:
(1)、【规律探究】:探究一
探究二
探究三
∵ ,
∴ ,
∴ .
∵ ,
∴ ,
∴ , .
∵ ,
∴ ,
∴ , .
(2)、【结论归纳】. (用含n的式子表示)
25. 已知:如图,在矩形ABCD中,AB=24cm,BC=16cm,点E为边CD的中点,连接BE , EF⊥BE交AD于点F . 点P从点B出发,沿BE方向匀速运动,速度为2cm/s;同时,点Q从点A出发,沿AB方向匀速运动,速度为3cm/s.当一个点停止运动时,另一个点也停止运动.设运动时间为t(s)(0<t<8).解答下列问题: (1)、当t为何值时,点P在线段BQ的垂直平分线上?(2)、连接PQ , 设五边形AFEPQ的面积为y(cm2),求y与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t , 使S五边形AFEPQ∶S矩形ABCD=33∶64?若存在,求出t的值;若不存在,请说明理由;(4)、在运动过程中,是否存在某一时刻t , 使点Q在∠AFE的平分线上?若存在,求出t的值;若不存在,请说明理由.
(1)、当t为何值时,点P在线段BQ的垂直平分线上?(2)、连接PQ , 设五边形AFEPQ的面积为y(cm2),求y与t的函数关系式;(3)、在运动过程中,是否存在某一时刻t , 使S五边形AFEPQ∶S矩形ABCD=33∶64?若存在,求出t的值;若不存在,请说明理由;(4)、在运动过程中,是否存在某一时刻t , 使点Q在∠AFE的平分线上?若存在,求出t的值;若不存在,请说明理由.