甘肃省定西市2023-2024学年九年级上学期12月月考数学试题

试卷更新日期：2024-01-12 类型：月考试卷

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分，每小题只有一个正确选项．

1. $- 7$ 的绝对值是（）

A、7 B、 $\frac{1}{7}$ C、 $- 7$ D、 $- \frac{1}{7}$

查看试题解析
2. 在下列交通标志中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 中国空间站每天绕地球19圈，大约96分钟绕一圈，即速度为78000米/秒，将78000用科学记数法表示应为（）

A、 $0.78 \times 1 0^{5}$ B、 $7.8 \times 1 0^{5}$ C、 $7.8 \times 1 0^{4}$ D、 $78 \times 1 0^{3}$

查看试题解析
4. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{2} = 2$ B、 $\sqrt{20} \div \sqrt{5} = 4$ C、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$ D、 $\sqrt{12} = 3 \sqrt{2}$

查看试题解析
5. 不等式 $2 x + 5 < - 1$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 定义一种运算“※”： $x ※ y = 2 x - y - 1$ （其中x ， y为任意实数）．当 $a ※ b = 3$ 时，则 $(5 + 2 a) ※ (2 b)$ 的值为（）

A、7 B、 $10$ C、 $17$ D、 $31$

查看试题解析
7. 已知关于x的一元二次方程（a+1）x²﹣2x+a²+a＝0有一个根为x＝0，则a的值为（）

A、0 B、0或﹣1 C、1 D、﹣1

查看试题解析
8. 将直线 $y = 5 x$ 向下平移2个单位长度，所得直线的表达式为（）

A、 $y = 5 x - 2$ B、 $y = 5 x + 2$ C、 $y = 5 (x + 2)$ D、 $y = 5 (x - 2)$

查看试题解析
9. 如图，点 $A ， B ， C ， D ， E$ 在 $⊙ O$ 上， $A B = C D ， ∠ A O B = 42 °$ ，则 $∠ C E D =$ （）

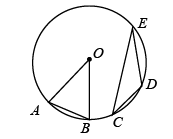A、48° B、24° C、22° D、21°

查看试题解析
10. 如图，在矩形 $A B C D$ 中， $A B = 3 ， B C = 2$ ， E为 $A B$ 的中点，动点P从点C出发，沿 $C D \to D A \to A E$ 向点E运动，连接 $P E ， P C ， C E$ ．设点P的运动路程为x ， $△ P C E$ 的面积为y ，则下列能大致反映y与x之间函数关系的图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题：本大题共6小题，每小题3分，共18分．

11. 因式分解： $2 m^{2} - 8 n^{2} =$ ．

查看试题解析
12. 函数y= $\frac{\sqrt{x + 2}}{x - 1}$ 中自变量x的取值范围是．

查看试题解析
13. 若正六边形的内切圆半径为2，则其外接圆半径为．

查看试题解析
14. 如图，从一块直径为 $4dm$ 的圆形铁皮上剪出一个圆心角为 $90 °$ 的扇形，则此扇形的面积为 ${dm}^{2}$ .

查看试题解析
15. 函数 $y = a x$ 和 $y = k x + b$ 的图象相交于点 $A (- 2 ， 1)$ ，则方程 $a x = k x + b$ 的解为．

查看试题解析
16. 如图，在平面直角坐标系中，矩形 $O A B C$ 的两边 $O A$ ， $O C$ 分别在 $x$ 轴和 $y$ 轴上，并且 $O A = 5$ ， $O C = 3$ .若把矩形 $O A B C$ 绕着点 $O$ 逆时针旋转，使点 $A$ 恰好落在 $B C$ 边上的 $A_{1}$ 处，则点 $A_{1}$ 的坐标为.

查看试题解析

三、解答题本大题共6小题，共32分．解答应写出必要的文字说明，证明过程或演算步骤．

17. 计算： $| 1 - \sqrt{2} | + {(\frac{1}{2})}^{- 2} + {(- 2)}^{0}$ ．

查看试题解析
18. 解方程：

(1)、 $x^{2} = - 2 x$ ；

(2)、 $x^{2} - 9 x + 20 = 0$ ．

查看试题解析
19. 化简求值： $\frac{m^{2} - 1}{m^{2} + 2 m + 1} \div (\frac{m}{m + 1} - 1)$ ，其中 $m = - 2$

查看试题解析
20. 如图所示，要把残破的轮片复制完整，已知弧上的三点A ， B ， C ．

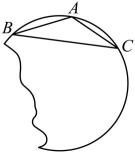(1)、用尺规作图法找出所在圆的圆心；（保留作图痕迹，不写作法）

(2)、设 $△ A B C$ 是等腰三角形，底边 $B C = 8 c m$ ，腰 $A B = 5 c m$ ，求圆片的半径R ．

查看试题解析
21. 书籍是人类宝贵的精神财富，读书则是传承优秀文化的通道．某中学为响应“全民阅读活动”，利用节假日面向社会开放学校图书馆．据统计，第一个月进馆250人次，进馆人次逐月增加，第三个月进馆360人次．若进馆人次的月平均增长率相同，求进馆人次的月平均增长率．

查看试题解析
22. 如果圆锥的底面圆的周长是 $20 π$ ，侧面展开后所得的扇形的圆心角为 $120 °$ ，求该圆锥的侧面积和全面积．

查看试题解析

四、解答题本大题共5小题，共40分．解答应写出必要的文字说明，证明过程或演算步骤．

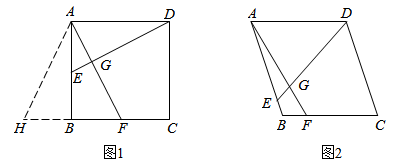
23. 如图， $△ A B C$ 为等边三角形， $△ A B C$ 绕点A逆时针旋转得 $△ A C D$ ，且 $B P = C Q$ ．

(1)、求证： $△ A B P ≅ △ A C Q$ ；

(2)、求 $∠ A P Q$ 的度数．

查看试题解析
24. 2022年在中国举办的冬奥会和残奥会令世界瞩目，冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓，成为热销产品．某商家以每30元的价格购进一批冰墩墩和雪容融套件．若该产品每套的售价40元时，每天可售出200套；若每套售价提高1元，则每天少卖2套．

(1)、设冰墩墩和雪容融套件每套售价定为x元，求该商品销售量y与x之间的函数关系式；

(2)、求每套售价定为多少元时，每天销售套件所获利润W最大，最大利润是多少元？

查看试题解析
25. 已知 $B C$ 是 $⊙ O$ 的直径，点D是 $B C$ 延长线上一点， $A B = A D$ ， $A E$ 是 $⊙ O$ 的弦， $∠ A E C = 30 °$ ．

(1)、求证：直线 $A D$ 是 $⊙ O$ 的切线；

(2)、若 $A E ⊥ B C$ ，垂足为M ， $⊙ O$ 的半径为10，求 $A E$ 的长．

查看试题解析
26. 问题解决：如图1，在矩形 $A B C D$ 中，点 $E ， F$ 分别在 $A B ， B C$ 边上， $D E = A F ， D E ⊥ A F$ 于点 $G$ .

(1)、求证：四边形 $A B C D$ 是正方形；

(2)、延长 $C B$ 到点 $H$ ，使得 $B H = A E$ ，判断 $△ A H F$ 的形状，并说明理由.
类比迁移：如图2，在菱形 $A B C D$ 中，点 $E ， F$ 分别在 $A B ， B C$ 边上， $D E$ 与 $A F$ 相交于点 $G$ ， $D E = A F ， ∠ A E D = 60 ° ， A E = 6 ， B F = 2$ ，求 $D E$ 的长.

查看试题解析
27. 已知直线 $y = - x + 3$ 与x轴相交于点A，与y轴相交于点B.经过A，B两点的抛物线 $y = a x^{2} + b x + c$ 的对称轴为直线 $x = 1$ ，与x轴的另一个交点为D（D在A左侧），点P为y轴右侧抛物线上的一动点.

(1)、求抛物线的解析式；

(2)、若Q为 $O A$ 的中点，当 $P Q / / y$ 轴时，求点P的坐标；

(3)、当点P位于直线 $A B$ 上方的抛物线上时，求四边形 $P A D B$ 面积的最大值.

查看试题解析