江西省宜春市丰城市2022-2023学年高一上学期期末数学试题

试卷更新日期：2024-01-11 类型：期末考试

进入出卷网下载

一、单选题（每题5分共40分）

1. 已知集合 $A = {- 1 ， 0 ， 1 ， 2}$ ， $B = {x ∣ 0 < x < 3}$ ，则 $A ∩ B =$ （）

A、 ${- 1 ， 2}$ B、 ${1 ， 2}$ C、 ${0 ， 1}$ D、 ${0 ， 1 ， 2}$

查看试题解析
2. 设 $x > 0$ ， $y > 0$ ，且 $x y = 4$ ，求 $\frac{1}{x} + \frac{1}{y}$ 的最小值是（）

A、1 B、2 C、 $- 1$ D、 $- 2$

查看试题解析
3. 已知一组数据 $x_{1} ， x_{2} ， \cdot \cdot \cdot ， x_{n}$ 的平均数为2，方差为1；则 $3 x_{1} + 2 ， 3 x_{2} + 2 ， \cdot \cdot \cdot ， 3 x_{n} + 2$ 的平均数和方差分别为（）

A、2，1 B、8，3 C、8，5 D、8，9

查看试题解析
4. 下列叙述：①某人射击1次，“射中7环”与“射中8环”是互斥事件；
②甲、乙两人各射击1次，“至少有1人射中目标”与“没有人射中目标”是对立事件；
③抛掷一枚硬币，连续出现4次正面向上，则第5次出现反面向上的概率大于 $\frac{1}{2}$ ；
④在相同条件下，进行大量重复试验，可以用频率来估计概率；则所有正确结论的序号是（）

A、①②④ B、①③ C、②④ D、①②

查看试题解析
5. 已知偶函数 $f (x) = {\begin{array}{l} 3^{x} + a ， x \geq 0 \\ g (x) ， x < 0 \end{array}$ ，则满足 $f (x - 1) < f (2)$ 的实数 $x$ 的取值范围是（）

A、 $(- \infty ， 3)$ B、 $(3 ， + \infty)$ C、 $(- 1 ， 3)$ D、 $(- \infty ， - 1) \cup (3 ， + \infty)$

查看试题解析
6. 设 $a = 7^{0.3}$ ， $b = 0 . 3^{7}$ ， $c = l n 0.3$ ，则 $a$ ， $b$ ， $c$ 的大小关系为（）

A、 $c < a < b$ B、 $c < b < a$ C、 $a < b < c$ D、 $a < c < b$

查看试题解析
7. 某高校组织大学生知识竞赛，共设有5个版块的试题，分别是“中华古诗词”“社会主义核心价值观”“科学实践观”“中国近代史”及“创新发展能力”.某参赛队从中任选2个版块作答，则“创新发展能力”版块被该队选中的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{5}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
8. 函数 $f (x) = l n x - \frac{2}{x}$ 的零点所在的大致区间是（）

A、 $(\frac{1}{e} ， 1)$ B、 $(1 ， 2)$ C、 $(2 ， 3)$ D、 $(e ， + ∞)$

查看试题解析

二、多选题（每题5分共20分）

9. 某公司为了解用户对其产品的满意度，随机调查了10个用户，得到用户对产品的满意度评分如下表所示，评分用区间[0，10]内的一个数来表示，该数越接近10表示满意度越高，则下列说法正确的是（）
7
8
9
7
5
4
10
9
4
7

A、这组数据的平均数为6 B、这组数据的众数为7 C、这组数据的极差为6 D、这组数据的75%分位数为9

查看试题解析
10. 已知函数 $f (x) = \frac{1}{| x | - 2}$ ，则下列结论中正确的是（）

A、 $f (x)$ 是偶函数 B、 $f (x)$ 在 $(- \infty ， - 2)$ 上单调递增 C、 $f (x)$ 的值域为R D、当 $x \in (- 2 ， 2)$ 时， $f (x)$ 有最大值

查看试题解析
11. 已知函数 $f (x) = {\begin{array}{l} l g (- x) ， x < 0 \\ e^{x - 1} ， x \geq 0 \end{array}$ ，若 $f (1) + f (a) = 2$ ，则 $a$ 的所有可能值为（）

A、1 B、 $- 1$ C、10 D、 $- 10$

查看试题解析
12. 从甲袋中摸出一个红球的概率是 $\frac{1}{3}$ ，从乙袋中摸出一个红球的概率是 $\frac{1}{2}$ ，从两袋各摸出一个球，下列结论正确的是（）

A、2个球都是红球的概率为 $\frac{1}{6}$ B、2个球不都是红球的概率为 $\frac{1}{3}$ C、至少有1个红球的概率为 $\frac{2}{3}$ D、2个球中恰有1个红球的概率为 $\frac{1}{2}$

查看试题解析

三、填空题（每题5分共20分）

13. 某单位有男女职工共 $600$ 人，现用分层抽样的方法从所有职工中抽取容量为 $50$ 的样本，已知从女职工中抽取的人数为 $15$ ，那么该单位的女职工人数为．

查看试题解析
14. 已知甲，乙，丙三人去参加某公司面试，他们被该公司录取的概率分别是 $\frac{1}{6} ， \frac{1}{4} ， \frac{1}{3}$ ，且三人录取结果相互之间没有影响，则他们三人中至少有一人被录取的概率为.

查看试题解析
15. 某公司16个销售店某月销售产品数量 $($ 单位：台 $)$ 的茎叶图如图所示，已知数据落在 $[18 ， 22]$ 中的频率为 $0.25$ ， $75 %$ 分位数为 .

查看试题解析
16. 若关于 $x$ 的不等式 $a x^{2} + b x - 1 > 0$ 的解集是 ${x | 1 < x < 2}$ ，则不等式 $b x^{2} + a x - 1 < 0$ 的解集是；

查看试题解析

四、解答题

17. 计算：

(1)、 $0.02 7^{- \frac{1}{3}} - {(- \frac{1}{7})}^{- 2} + 1 6^{\frac{3}{2}} - 3^{- 1} + 2 \cdot {(\sqrt{3} - 1)}^{0}$ .

(2)、 $\frac{l g 8 + l g 125 - l g 2 - l g 5}{l g \sqrt{10} . l g 0.01}$

查看试题解析
18. 甲、乙两名射击运动员进行射击比赛，甲的中靶概率为0.8，甲、乙都中靶的概率为0.72，求下列事件的概率；

(1)、乙中靶；

(2)、恰有一人中靶；

(3)、至少有一人中靶.

查看试题解析
19. 已知函数 $f (x) = (m^{2} - 2 m - 2) \cdot m^{x}$ 是指数函数.

(1)、求实数 $m$ 的值；

(2)、解不等式 ${(2 + x)}^{\frac{m}{2}} < {(1 - x)}^{\frac{m}{2}}$

查看试题解析
20. 已知幂函数 $f (x) = (a^{2} - 3 a + 3) x^{a}$ 为偶函数，

(1)、求函数 $f (x)$ 的解析式；

(2)、若函数 $g (x) = f (x) + (2 m - 1) x - 3$ 在 $[- 1 ， 3]$ 上的最大值为2，求实数 $m$ 的值．

查看试题解析
21. 文明城市是反映城市整体文明水平的综合性荣誉称号，作为普通市民，既是文明城市的最大受益者，更是文明城市的主要创造者，某市为提高市民对文明城市创建的认识，举办了“创建文明城市”知识竞赛，从所有答卷中随机抽取100份作为样本，将样本的成绩（满分100分，成绩均为不低于40分的整数）分成六段： $[40 ， 50)$ $[50 ， 60)$ ， …， $[90 ， 100]$ ，得到如图所示的频率分布直方图.

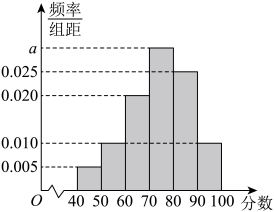(1)、求频率分布直方图中a的值；

(2)、求样本成绩的第75百分位数；

(3)、已知落在 $[50 ， 60)$ 的平均成绩是54，方差是7，落在 $[60 ， 70)$ 的平均成绩为66，方差是4，求两组成绩的总平均数 $\bar{z}$ .

查看试题解析
22. 为了解某年级学生对《居民家庭用电配置》的了解情况，校有关部门在该年级进行了一次问卷调查(共10道题)，从该年级学生中随机抽取24人，统计了每人答对的题数，将统计结果分成[0，2)，[2，4)，[4，6)，[6，8)，[8，10]五组，得到如下频率分布直方图.

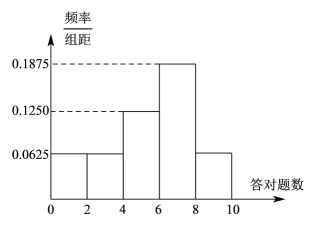(1)、估计这组数据的平均数(同一组中的数据用该组区间的中点值作代表)；

(2)、用分层随机抽样的方法从[4，6)，[6，8)，[8，10]的组别中共抽取12人，分别求出抽取的三个组别的人数；

(3)、若从答对题数在[2，6)内的人中随机抽取2人，求恰有1人答对题数在[2，4)内的概率.

查看试题解析