吉林省吉林市重点中学2022-2023学年高一(平行班)上学期期末测试数学试题
试卷更新日期:2024-01-10 类型:期末考试
一、单项选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项符合要求.
-
1. 已知集合 , 那么( )A、 B、 C、 D、2. 下列函数是奇函数,且在上单调递增的是( )A、 B、 C、 D、3. 已知扇形的弧长为1,面积为2,则该扇形的圆心角的弧度为( )A、 B、 C、2 D、44. 设 , 则的值为( )A、8 B、9 C、10 D、115. 幂函数的图象过点 , 则它在上的最小值为( )A、-2 B、-1 C、1 D、6. 科学家以里氏震级来度量地震的强度,若设Ⅰ为地震时所散发出来的相对能量程度,则里氏震级y可定义为 , 2021年3月13日下午江西鹰潭余江区发生里氏3.1级地震,2020年1月1日四川自贡发生里氏4.9级地震,则自贡地震所散发出来的能量是余江地震所散发出来的能量的( )倍.A、2 B、10 C、100 D、10007. 在同一平面直角坐标系中,函数 , (且)的图象可能是( )A、
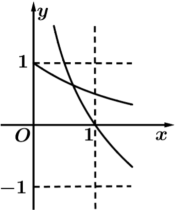 B、
B、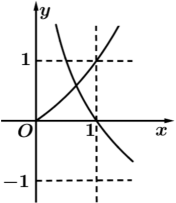 C、
C、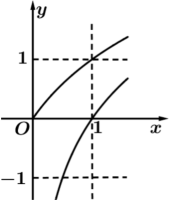 D、
D、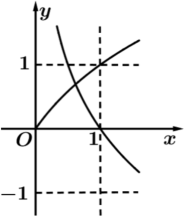 8. 已知 , 则( )A、 B、 C、 D、39. 设是定义域为的偶函数,且在单调递减,设 , 则( )A、 B、 C、 D、10. 在西双版纳热带植物园中有一种原产于南美热带雨林的时钟花,其花开花谢非常有规律.有研究表明,时钟花开花规律与温度密切相关,时钟花开花所需要的温度约为 , 但当气温上升到时,时钟花基本都会凋谢.在花期内,时钟花每天开闭一次.已知某景区有时钟花观花区,且该景区6时时的气温(单位:)与时间(单位:小时)近似满足函数关系式 , 则在6时时中,观花的最佳时段约为( )(参考数据:)
8. 已知 , 则( )A、 B、 C、 D、39. 设是定义域为的偶函数,且在单调递减,设 , 则( )A、 B、 C、 D、10. 在西双版纳热带植物园中有一种原产于南美热带雨林的时钟花,其花开花谢非常有规律.有研究表明,时钟花开花规律与温度密切相关,时钟花开花所需要的温度约为 , 但当气温上升到时,时钟花基本都会凋谢.在花期内,时钟花每天开闭一次.已知某景区有时钟花观花区,且该景区6时时的气温(单位:)与时间(单位:小时)近似满足函数关系式 , 则在6时时中,观花的最佳时段约为( )(参考数据:) A、时时 B、时时 C、时时 D、时时
A、时时 B、时时 C、时时 D、时时二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
-
11. 下列说法正确的是( )A、函数的定义域是 B、函数在其定义域上单调递减 C、函数的值域是 D、函数的图象过定点12. 下列结论中正确的有( )A、若命题“ , ”为假命题,则实数的取值范围是 B、若 , 则“”的充要条件是“” C、“”是“”的充分不必要条件 D、当时,的最小值为13. 下列各式中,值为的是( )A、 B、 C、 D、14. 函数的部分图象如图中实线所示,图中圆与的图象交于 , 两点,且在轴上,则下列说法中正确的是( )
 A、函数在上单调递减 B、函数的最小正周期是 C、函数的图象向左平移个单位后关于直线对称 D、若圆半径为 , 则函数的解析式为
A、函数在上单调递减 B、函数的最小正周期是 C、函数的图象向左平移个单位后关于直线对称 D、若圆半径为 , 则函数的解析式为三、填空题:本大题共6个小题,每小题5分,共30分.
-
15. 计算: .16. 已知角的顶点在坐标原点,始边与x轴的非负半轴重合,终边经过点 , 则 .17. 已知为钝角,为钝角满足 , 则 .18. 已知函数是定义在上的增函数,并且满足 . 若 , 求x的取值范围 .19. 已知函数 , 则函数的对称轴的方程为 .20. 已知函数的图象过点 , 若在内有4个零点,则a的取值范围为 .
四、解答题:共50分.解答应写出文字说明,证明过程或演算步骤.
-
21. 已知关于x的不等式的解集为 .(1)、求实数m的值;(2)、正实数a , b满足 , 求的最小值.22. 某公司设计了某款新产品,为生产该产品需要引进新型设备.已知购买该新型设备需要3万元,之后每生产x万件产品,还需另外投入原料费及其他费用万元,产量不同其费用也不同,且已知每件产品的售价为8元且生产的该产品可以全部卖出.(1)、写出年利润(万元)关于年产量x(万件)的函数解析式;(2)、该产品年产量为多少万件时,公司所获年利润最大?其最大利润为多少万元?