黑龙江省哈尔滨市香坊区2023-2024学年高三上学期期末联考数学试卷
试卷更新日期:2024-01-10 类型:期末考试
一、、单选题:本题共8个小题,在每个小题给出的四个选项中,只有一项是符合要求的.
-
1. 已知为虚数单位,若复数 , 则( )A、复数实部为1 B、复数虚部为0 C、 D、在复平面内对应的点位于第二象限2. 已知集合 , 集合 , 则集合( )A、 B、 C、 D、3. 已知直线 , 平面 , , , , , 则是的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件4. 设函数 , 已知方程在上有且仅有2个根,则的取值范围是( )A、 B、 C、 D、5. 下列函数的图象不可能与直线相切的是( )A、 B、 C、 D、6. 已知函数且为奇函数,则( )A、 B、 C、2 D、47. 过正四棱锥的高的中点作平行于底面的截面 , 若四棱锥与四棱台的表面积之比为 , 则直线与底面所成角的余弦值为( )A、 B、 C、 D、8. 在平面直角坐标系Oxy中,A为直线l:上在第一象限内的点, , 以AB为径的圆C与直线交于另一点.若 , 则A点的横坐标为( )A、 B、3 C、3或 D、2
二、、多选题:本题共4个小题,在每个小题给出的选项中,有多个符合题目要求.
-
9. 已知椭圆的左右焦点分别为 , 点在椭圆内部,点在椭圆上,则以下说法正确的是( )A、离心率的取值范围为 B、的最小值为4 C、不存在点 , 使得 D、当时,以点为中点的椭圆的弦的斜率为110. 下列判断正确的是( )A、函数是定义在上的奇函数,若时, , 则时, B、若 , 则的取值范围是 C、为了得到函数的图象,可将函数图象上所有点的纵坐标缩短为原来的 , 横坐标不变,再向右平移1个单位长度 D、设满足满足 , 则11. 如图,在正四棱柱中, , 点分别是的中点,点是线段上的动点,则下列说法正确的是( )
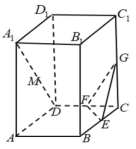 A、存在 , 使得平面 B、当时,存在 , 使得平面 C、存在 , 使得平面平面 D、存在 , 使得平面平面12. 已知数列 , 则( )A、当时,数列是公差为2的等差数列 B、当时,数列的前16项和为160 C、当时,数列前16项和等于72 D、当时,数列的项数为偶数时,偶数项的和大于奇数项的和
A、存在 , 使得平面 B、当时,存在 , 使得平面 C、存在 , 使得平面平面 D、存在 , 使得平面平面12. 已知数列 , 则( )A、当时,数列是公差为2的等差数列 B、当时,数列的前16项和为160 C、当时,数列前16项和等于72 D、当时,数列的项数为偶数时,偶数项的和大于奇数项的和三、、填空题:本题4个小题.
-
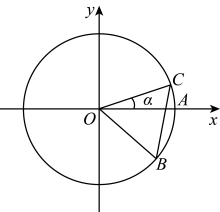
13. 若向量满足 , 且在上的投影向量为 , 则.14. 已知数列{an}满足a4+a7=2,a5a6=﹣8,若{an}是等差数列,则a1a10=;若{an}是等比数列,则a1+a10=.15. 如图,圆与轴的正半轴的交点为 , 点 , 在圆上,且点位于第一象限,点的坐标为 , .若 , 则的值为.
 16. 已知椭圆的左顶点 , 左焦点 , 过的右焦点做轴的垂线,为垂线上一点,当椭圆的离心率为时,最大值为.
16. 已知椭圆的左顶点 , 左焦点 , 过的右焦点做轴的垂线,为垂线上一点,当椭圆的离心率为时,最大值为.四、解答题:解答题写出文字说明、证明过程或演算步骤.
-
17. 已知双曲线的实轴长为4,且与双曲线有公共的焦点.(1)、求双曲线的方程;(2)、已知 , 是双曲线上的任意一点,求的最小值.18. 如图,在三棱柱中, , 顶点在底面上的射影恰为点 , 且 .
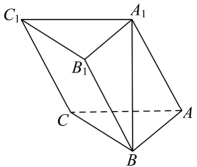 (1)、证明:平面;(2)、是线段中点,求平面和平面夹角的余弦值.19. 已知在数列中, .(1)、令 , 证明:数列是等比数列;(2)、设 , 证明:数列是等差数列.20. 在中, , 点A在线段上, , 且 , ,
(1)、证明:平面;(2)、是线段中点,求平面和平面夹角的余弦值.19. 已知在数列中, .(1)、令 , 证明:数列是等比数列;(2)、设 , 证明:数列是等差数列.20. 在中, , 点A在线段上, , 且 , ,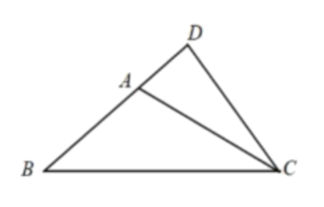 (1)、求的值;(2)、求的值和的面积.21. “工艺折纸”是一种把纸张折成各种不同形状物品的艺术活动,在我国源远流长.某些折纸活动蕴含丰富的数学内容,例如:用一张圆形纸片,按如下步骤折纸(如图)
(1)、求的值;(2)、求的值和的面积.21. “工艺折纸”是一种把纸张折成各种不同形状物品的艺术活动,在我国源远流长.某些折纸活动蕴含丰富的数学内容,例如:用一张圆形纸片,按如下步骤折纸(如图)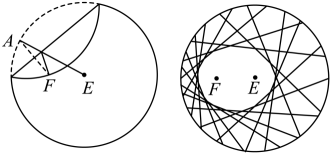
步骤1:设圆心是 , 在圆内异于圆心处取一点,标记为;
步骤2:把纸片折叠,使圆周正好通过点;
步骤3:把纸片展开,并留下一道折痕;
步骤4:不停重复步骤2和3,就能得到越来越多的折痕.
现对这些折痕所围成的图形进行建模研究.若取半径为6的圆形纸片,如图,设定点到圆心的距离为4,按上述方法折纸.以点所在的直线为轴,线段中点为原点建立平面直角坐标系.
(1)、若已研究出折痕所围成的图形即是折痕与线段交点的轨迹,求折痕围成的椭圆的标准方程;(2)、记(1)问所得图形为曲线 , 若过点且不与轴垂直的直线与椭圆交于两点,在轴的正半轴上是否存在定点 , 使得直线斜率之积为定值?若存在,求出该定点和定值;若不存在,请说明理由.22. 已知 , 函数 , .(1)、讨论函数的单调性;(2)、设是的导数.证明:(i)在上单调递增;
(ii)当时,若 , 则.