广东省广州市2024届高三上学期12月调研考试（零模）数学（B）

试卷更新日期：2024-01-10 类型：高考模拟

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 已知复数 $z$ 满足 $z + \bar{z} = 2$ ， $z - \bar{z} = - 4 i$ ，则 $| z | =$ （）

A、1 B、2 C、 $\sqrt{5}$ D、 $2 \sqrt{5}$

查看试题解析
2. 已知集合 $M = {x | y = l n (1 - 2 x)}$ ， $N = {y | y = e^{x}}$ ，则 $M \cap N =$ （）

A、 $(0 ， \frac{1}{2})$ B、 $(- \infty ， \frac{1}{2})$ C、 $(\frac{1}{2} ， + \infty)$ D、 $\emptyset$

查看试题解析
3. 已知向量 $\vec{a} = (- 2 ， 4)$ ， $\vec{b} = (1 ， t)$ ，若 $\vec{a}$ 与 $\vec{b}$ 共线，则向量 $\vec{a} + \vec{b}$ 在向量 $\vec{j} = (0 ， 1)$ 上的投影向量为（）

A、 $\vec{j}$ B、 $- \vec{j}$ C、 $2 \vec{j}$ D、 $- 2 \vec{j}$

查看试题解析
4. 已知函数 $f (x) = a + \frac{b}{3^{x} - 1} (a b \neq 0)$ 是奇函数，则（）

A、 $2 a + b = 0$ B、 $2 a - b = 0$ C、 $a + b = 0$ D、 $a - b = 0$

查看试题解析
5. 如图的形状出现在南宋数学家杨辉所著的《详解九章算法·商功》中，后人称为“三角垛”．“三角垛”的最上层有1个球，第二层有3个球，第三层有6个球，……．记各层球数构成数列 ${a_{n}}$ ，且 ${a_{n + 1} - a_{n}}$ 为等差数列，则数列 ${\frac{1}{a_{n}}}$ 的前 $100$ 项和为（）

A、 $\frac{99}{100}$ B、 $\frac{100}{101}$ C、 $\frac{99}{50}$ D、 $\frac{200}{101}$

查看试题解析
6. 直线 $l ： y = k x - 2$ 与圆 $C ： x^{2} + y^{2} - 6 x - 7 = 0$ 交于A ， B两点，则 $| A B |$ 的取值范围为（）

A、 $[\sqrt{7} ， 4]$ B、 $[2 \sqrt{7} ， 8]$ C、 $[\sqrt{3} ， 4]$ D、 $[2 \sqrt{3} ， 8]$

查看试题解析
7. 已知 $0 < β < α < \frac{π}{2}$ ， $c o s (α + β) = \frac{1}{5}$ ， $s i n (α - β) = \frac{3}{5}$ ，则 $t a n α t a n β$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{5}$ C、 $\frac{5}{3}$ D、2

查看试题解析
8. 若函数 $f (x) = \frac{1}{3} x^{3} - a x^{2} + x + 1$ 在区间 $(0 ， 2)$ 上存在极小值点，则a的取值范围为（）

A、 $(1 ， \frac{5}{4})$ B、 $[1 ， \frac{5}{4})$ C、 $[\frac{5}{4} ， 2)$ D、 $(1 ， + \infty)$

查看试题解析

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得2分．

9. 某市实行居民阶梯电价收费政策后有效促进了节能减排.现从某小区随机调查了200户家庭十月份的用电量(单位：kW·h)，将数据进行适当分组后(每组为左闭右开的区间)，画出如图所示的频率分布直方图，则（）

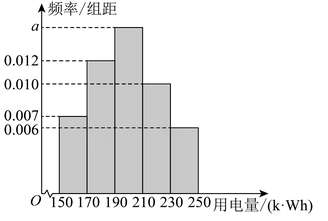A、图中a的值为0.015 B、样本的第25百分位数约为217 C、样本平均数约为198.4 D、在被调查的用户中，用电量落在［170，230)内的户数为108

查看试题解析
10. 已知双曲线 $E ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{2} = 1 (a > 0)$ 的左、右焦点别为 $F_{1}$ ， $F_{2}$ ，过点 $F_{2}$ 的直线l与双曲线 $E$ 的右支相交于 $P ， Q$ 两点，则（）

A、若 $E$ 的两条渐近线相互垂直，则 $a = \sqrt{2}$ B、若 $E$ 的离心率为 $\sqrt{3}$ ，则 $E$ 的实轴长为 $1$ C、若 $∠ F_{1} P F_{2} = 90 °$ ，则 $| P F_{1} | \cdot | P F_{2} | = 4$ D、当 $a$ 变化时， $△ F_{1} P Q$ 周长的最小值为 $8 \sqrt{2}$

查看试题解析
11. 已知点 $P (\frac{3 π}{8} ， 1)$ 是函数 $f (x) = s i n (ω x + \frac{π}{4}) + b (ω > 0)$ 的图象的一个对称中心，则（）

A、 $f (x - \frac{3 π}{8}) - 1$ 是奇函数 B、 $ω = - \frac{2}{3} + \frac{8}{3} k$ ， $k \in N^{*}$ C、若 $f (x)$ 在区间 $(\frac{3 π}{8} ， \frac{11 π}{8})$ 上有且仅有 $2$ 条对称轴，则 $ω = 2$ D、若 $f (x)$ 在区间 $(\frac{π}{5} ， \frac{2 π}{5})$ 上单调递减，则 $ω = 2$ 或 $ω = \frac{14}{3}$

查看试题解析
12. 如图，在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，已知M ， N ， P分别是棱 $C_{1} D_{1}$ ， $A A_{1}$ ， $B C$ 的中点，Q为平面 $P M N$ 上的动点，且直线 $Q B_{1}$ 与直线 $D B_{1}$ 的夹角为 $30 °$ ，则（）

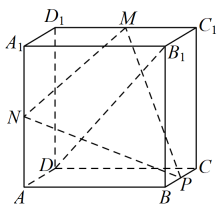A、 $D B_{1} ⊥$ 平面 $P M N$ B、平面 $P M N$ 截正方体所得的截面面积为 $3 \sqrt{3}$ C、点Q的轨迹长度为 $π$ D、能放入由平面PMN分割该正方体所成的两个空间几何体内部（厚度忽略不计）的球的半径的最大值为 $\frac{3 - \sqrt{3}}{2}$

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分．

13. 已知抛物线 $C ： y^{2} = 2 p x (p > 0)$ 的焦点为F ，点M在C上， $M F ⊥ x$ 轴，若 $△ O F M$ （O为坐标原点）的面积为2，则 $p =$ .

查看试题解析
14. ${(2 x^{2} + x - y)}^{5}$ 的展开式中 $x^{5} y^{2}$ 的系数为（用数字作答）.

查看试题解析
15. 已知三棱锥 $P - A B C$ 的四个顶点均在同一球面上， $P C ⊥$ 平面 $A B C$ ， $P C = B C = \sqrt{6}$ ， $A B = 2 \sqrt{6}$ ，且 $P A$ 与平面 $A B C$ 所成角的正弦值为 $\frac{\sqrt{6}}{6}$ ，则该球的表面积为.

查看试题解析
16. 已知函数 $f (x) = e^{2 x} - 2 a (x - 2) e^{x} - a^{2} x^{2} (a > 0)$ 恰有两个零点，则 $a =$ .

查看试题解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤．

17. 设数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且 $S_{n} = 2 a_{n} - 1$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若数列 ${b_{n}}$ 满足 $b_{n} = {\begin{array}{l} l o g_{2} a_{n} ， n 为奇数 \\ a_{n} ， n 为偶数 \end{array}$ ，求数列 ${b_{n}}$ 的前2n项和 $T_{2 n}$ .

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中， $C D / / A B$ ， $∠ A B C = 90 °$ ， $A B = 2 B C = 2 C D = 4$ ，三棱锥 $B - P A D$ 的体积为 $\frac{4 \sqrt{2}}{3}$ .

(1)、求点 $P$ 到平面 $A B C D$ 的距离；

(2)、若 $P A = P D$ ，平面 $P A D ⊥$ 平面 $A B C D$ ，点 $N$ 在线段 $A P$ 上， $A N = 2 N P$ ，求平面 $N C D$ 与平面 $A B C D$ 夹角的余弦值.

查看试题解析
19. 记 $△ A B C$ 的内角A ， B ， C的对边分别为a ， b ， c ，已知 $b s i n B + c s i n C - a s i n A = 2 b s i n B s i n C$ 且 $C \neq \frac{π}{2}$ .

(1)、求证： $B = A + \frac{π}{2}$ ；

(2)、求 $c o s A + s i n B + s i n C$ 的取值范围.

查看试题解析
20. 已知函数 $f (x) = (x + 2) l n (x + 1) - a x$ .

(1)、当 $a = 0$ 时，求曲线 $y = f (x)$ 在点 $(0 ， f (0))$ 处的切线方程；

(2)、当 $- 1 < x < 0$ 时， $f (x) < 0$ ，求a的取值范围.

查看试题解析
21. 杭州亚运会的三个吉祥物是琮琮、宸宸和莲莲，他们分别代表了世界遗产良渚古城遗址、京杭大运河和西湖，分别展现了不屈不挠、坚强刚毅的拼搏精神，海纳百川的时代精神和精致和谐的人文精神. 甲同学可采用如下两种方式购买吉祥物，方式一：以盲盒方式购买，每个盲盒19元，盲盒外观完全相同，内部随机放有琮琮、宸宸和莲莲三款中的一个，只有打开才会知道买到吉祥物的款式，买到每款吉祥物是等可能的；方式二：直接购买吉祥物，每个30元.

(1)、甲若以方式一购买吉祥物，每次购买一个盲盒并打开. 当甲买到的吉祥物首次出现相同款式时，用X表示甲购买的次数，求X的分布列；

(2)、为了集齐三款吉祥物，甲计划先一次性购买盲盒，且数量不超过3个，若未集齐再直接购买吉祥物，以所需费用的期望值为决策依据，甲应一次性购买多少个盲盒?

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，点 $F (- \sqrt{3} ， 0)$ ，点 $P (x ， y)$ 是平面内的动点.若以PF为直径的圆与圆 $O ： x^{2} + y^{2} = 4$ 内切，记点P的轨迹为曲线E ．

(1)、求E的方程；

(2)、设点 $A (0 ， 1)$ ， $M (t ， 0)$ ， $N (4 - t ， 0) (t \neq 2)$ ，直线AM ， AN分别与曲线E交于点S ， T（S ， T异于A）， $A H ⊥ S T$ ，垂足为H ，求 $| O H |$ 的最小值．

查看试题解析

广东省广州市2024届高三上学期12月调研考试（零模） 数学（B）

一、选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得2分．

三、填空题：本题共4小题，每小题5分，共20分．

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤．

广东省广州市2024届高三上学期12月调研考试（零模）数学（B）