2023-2024学年浙教版数学八年级(上)期末仿真模拟卷(二)
试卷更新日期:2024-01-09 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 下列图标是节水、节能、低碳和绿色食品的标志,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下各组线段为边,能组成三角形的是( )A、2cm,4cm,6cm B、8cm,6cm,4cm C、14cm,6cm,7cm D、2cm,3cm,6cm3. 下列语句中,是命题的个数为( )
2. 以下各组线段为边,能组成三角形的是( )A、2cm,4cm,6cm B、8cm,6cm,4cm C、14cm,6cm,7cm D、2cm,3cm,6cm3. 下列语句中,是命题的个数为( )①若两个角相等,则它们是对顶角;②等腰三角形两底角相等;③画线段;④同角的余角相等;⑤同位角相等.
A、2个 B、3个 C、4个 D、5个4. 如图,中, , AD平分 , , , 垂足分别是E、F,则下列四个结论中:①AD上任意一点到B、C的距离相等;②AD任意一点到AB、AC的距离相等;③且;④ . 其中正确的是( )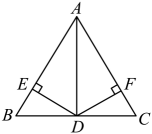 A、①④ B、②④ C、②③④ D、①②③④5. 以下数学表达式:①4x+3y>0;②x=3;③x2+xy+y2;④x≠5.其中不等式有( )A、4个 B、3个 C、2个 D、1个6. 若 , 则下列不等式成立的是( )A、 B、 C、 D、7. 在平面内,下列说法不能确定物体位置的是( )A、某影厅3排5座 B、北偏西30° C、某市解放路30号 D、东经110°,北纬30°8. 已知点A的坐标为(a+1,3﹣a),下列说法正确的是( )A、若点A在y轴上,则a=3 B、若点A在一三象限角平分线上,则a=1 C、若点A到x轴的距离是3,则a=±6 D、若点A在第四象限,则a的值可以为﹣29. 李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A、①④ B、②④ C、②③④ D、①②③④5. 以下数学表达式:①4x+3y>0;②x=3;③x2+xy+y2;④x≠5.其中不等式有( )A、4个 B、3个 C、2个 D、1个6. 若 , 则下列不等式成立的是( )A、 B、 C、 D、7. 在平面内,下列说法不能确定物体位置的是( )A、某影厅3排5座 B、北偏西30° C、某市解放路30号 D、东经110°,北纬30°8. 已知点A的坐标为(a+1,3﹣a),下列说法正确的是( )A、若点A在y轴上,则a=3 B、若点A在一三象限角平分线上,则a=1 C、若点A到x轴的距离是3,则a=±6 D、若点A在第四象限,则a的值可以为﹣29. 李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( ) A、金额 B、数量 C、单价 D、金额和单价10. 如图所示,直线y=x+3分别与x轴、y轴交于点A、B,若∠ABC=45°,则直线BC的函数表达式为( )
A、金额 B、数量 C、单价 D、金额和单价10. 如图所示,直线y=x+3分别与x轴、y轴交于点A、B,若∠ABC=45°,则直线BC的函数表达式为( )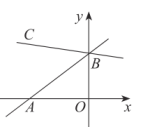 A、y=x+3 B、y=x+3 C、y=x+3 D、y=x+3
A、y=x+3 B、y=x+3 C、y=x+3 D、y=x+3二、填空题(每题4分,共24分)
-
11. 如图,∠BAF=46°,∠ACE=136°.CE⊥CD,则CD与AB平行的(填“是”或“不是”).
 12. 如图,BP、CP分别是∠ABC和∠ACB的平分线,过P点作EF∥BC ,EF分别交AB、AC于点E、F, PD⊥BC于点D . 下列结论:①;②C△AEF=AB+AC;③若AE+AF=m , PD=n,则三角形AEF的面积= . 其中正确的是 .
12. 如图,BP、CP分别是∠ABC和∠ACB的平分线,过P点作EF∥BC ,EF分别交AB、AC于点E、F, PD⊥BC于点D . 下列结论:①;②C△AEF=AB+AC;③若AE+AF=m , PD=n,则三角形AEF的面积= . 其中正确的是 . 13. 某业主贷款22000元购进一台机器,生产某种产品.已知产品的成本每个5元,售价是每个8元.若每月能生产、销售2000个产品,问至少个月后能赚回这台机器的贷款.14. 将点P(-1,2)向左平移2个单位,再向上平移1个单位所得的对应点的坐标为。15. 若直线下移后经过点(5,1),则平移后的直线解析式为 .16. 如图,在长方形中,点为坐标原点,点的坐标为 , 点 , 在坐标轴上,直线与交于点 , 与轴交于点 . 动点在边上,点是坐标平面内的点.当点在第一象限,且在直线上时,若是等腰直角三角形,则点的坐标为 .
13. 某业主贷款22000元购进一台机器,生产某种产品.已知产品的成本每个5元,售价是每个8元.若每月能生产、销售2000个产品,问至少个月后能赚回这台机器的贷款.14. 将点P(-1,2)向左平移2个单位,再向上平移1个单位所得的对应点的坐标为。15. 若直线下移后经过点(5,1),则平移后的直线解析式为 .16. 如图,在长方形中,点为坐标原点,点的坐标为 , 点 , 在坐标轴上,直线与交于点 , 与轴交于点 . 动点在边上,点是坐标平面内的点.当点在第一象限,且在直线上时,若是等腰直角三角形,则点的坐标为 .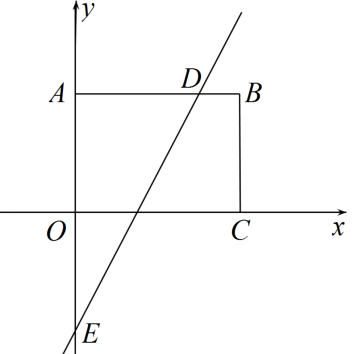
三、解答题(共8题,共66分)
-
17. 如图,AB=CD,DE⊥AC,BF⊥AC,点E,F是垂足,AE=CF,求证:
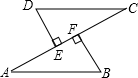 (1)、△ABF≌△CDE;(2)、AB∥CD.18. 如图,AD=BD,∠CAD+∠CBD=180°,求证:CD平分∠ACB.
(1)、△ABF≌△CDE;(2)、AB∥CD.18. 如图,AD=BD,∠CAD+∠CBD=180°,求证:CD平分∠ACB.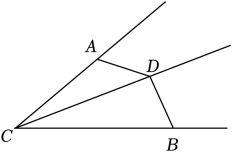 19.(1)、解方程:.(2)、解不等式组: , 并利用数轴确定不等式组的解集.20. 如图所示,在平面直角坐标系中,已知、、.
19.(1)、解方程:.(2)、解不等式组: , 并利用数轴确定不等式组的解集.20. 如图所示,在平面直角坐标系中,已知、、.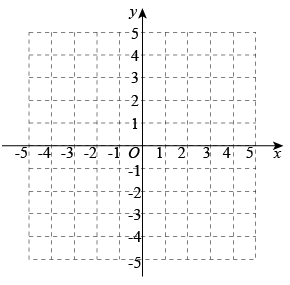 (1)、在平面直角坐标系中画出 , 则的面积是 ;(2)、若点D与点C关于y轴对称,则点D的坐标为;(3)、已知P为x轴正半轴上一点,若的面积为1,求点P的坐标.21. 某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题:
(1)、在平面直角坐标系中画出 , 则的面积是 ;(2)、若点D与点C关于y轴对称,则点D的坐标为;(3)、已知P为x轴正半轴上一点,若的面积为1,求点P的坐标.21. 某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示.根据图象解答下列问题: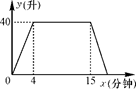 (1)、洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?(2)、已知洗衣机的排水速度为每分钟19升.
(1)、洗衣机的进水时间是多少分钟?清洗时洗衣机中水量为多少升?(2)、已知洗衣机的排水速度为每分钟19升.①求排水时洗衣机中的水量y(升)与时间x(分钟)与之间的关系式;
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量.
22. 小刚家近期准备换车,看中了价格相同的两款车,他对这两款车的部分信息做了调查,如下表所示:燃油车
新能源车
油箱容积:40升
电池电量:60千瓦时
油价:9元/升
电价:0.6元/千瓦时
续航里程:a千米
续航里程:a千米
每千米行驶费用:元
每千米行驶费用:____元
(续航里程指车辆在最大的能源储备下可连续行驶的总里程)
(1)、表中的新能源车每千米行驶费用为元(用含a的代数式表示);(2)、若燃油车的每千米行驶费用比新能源车多0.54元,分别求出两款车每千米行驶费用;(3)、在(2)的条件下,若燃油车和新能源车每年的其它费用分别为4800元和7500元.每年行驶里程至少超过千米时,使用新能源车的年费用更低(年费用=年行驶费用+年其它费用).23. 甲、乙两车从A城出发沿一条笔直公路匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.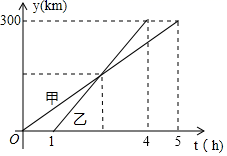 (1)、A,B两城相距千米,乙车比甲车早到小时;(2)、甲车出发多长时间与乙车相遇?(3)、若两车相距不超过30千米时可以通过无线电相互通话,则两车都在行驶过程中可以通过无线电通话的时间有多长?24. 定义:若三角形满足:两边的平方和与这两边乘积的差等于第三边的平方,则称这个三角形为“类勾股三角形”.如图1在中, , 则是“类勾股三角形”.
(1)、A,B两城相距千米,乙车比甲车早到小时;(2)、甲车出发多长时间与乙车相遇?(3)、若两车相距不超过30千米时可以通过无线电相互通话,则两车都在行驶过程中可以通过无线电通话的时间有多长?24. 定义:若三角形满足:两边的平方和与这两边乘积的差等于第三边的平方,则称这个三角形为“类勾股三角形”.如图1在中, , 则是“类勾股三角形”.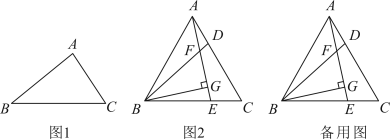 (1)、等边三角形一定是“类勾股三角形”,是命题(填真或假).(2)、若中, , 且 , 若是“类勾股三角形”,求的度数.(3)、如图2,在等边三角形的边上各取一点 , , 且相交于点 , 是的高,若是“类勾股三角形”,且.
(1)、等边三角形一定是“类勾股三角形”,是命题(填真或假).(2)、若中, , 且 , 若是“类勾股三角形”,求的度数.(3)、如图2,在等边三角形的边上各取一点 , , 且相交于点 , 是的高,若是“类勾股三角形”,且.①求证:.
②连结 , 若 , 那么线段能否构成一个“类勾股三角形”?若能,请证明;若不能,请说明理由.