江西省抚州市南城县2023-2024学年八年级上学期期中数学试题
试卷更新日期:2024-01-09 类型:期中考试
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
-
1. 下列实数是无理数的是( )A、 B、0 C、3.14 D、2. 下列等式正确的是( )A、 B、 C、 D、3. 如图,直角三角形三边向形外作了三个正方形,其中数字表示该正方形的面积,那么正方形的面积是( )
 A、360 B、164 C、400 D、604. 如图,一个三级台阶,它的每一级的长、宽和高分别为20、3、2,和是这个台阶两个相对的端点,点处有一只蚂蚁,想到点处去吃可口的食物,则蚂蚁沿着台阶面爬到点最短路程是( )
A、360 B、164 C、400 D、604. 如图,一个三级台阶,它的每一级的长、宽和高分别为20、3、2,和是这个台阶两个相对的端点,点处有一只蚂蚁,想到点处去吃可口的食物,则蚂蚁沿着台阶面爬到点最短路程是( ) A、20 B、15 C、25 D、275. 如图,在一次“寻宝”游戏中,寻宝人找到了如图所示的两个标志点A(3,1),B(2,2),则“宝藏”点C的位置是( )
A、20 B、15 C、25 D、275. 如图,在一次“寻宝”游戏中,寻宝人找到了如图所示的两个标志点A(3,1),B(2,2),则“宝藏”点C的位置是( )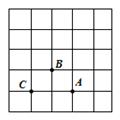 A、(1,0) B、(1,2) C、(2,1) D、(1,1)6. 如图,一只蚂蚁以均匀的速度沿台阶爬行,那么蚂蚁爬行时高度随时间变化的图象大致是( )
A、(1,0) B、(1,2) C、(2,1) D、(1,1)6. 如图,一只蚂蚁以均匀的速度沿台阶爬行,那么蚂蚁爬行时高度随时间变化的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(本大题共6小题,每小题3分,共18分.)
-
7. 16的算术平方根是8. 比较大小:24.(填“>”、“<”或“=”号)9. 已知点 , 点与点关于轴对称,则点的坐标是 .10. 一次函数图象与轴的交点坐标是 .11. 如图,正方形 的边 落在数轴上,点 表示的数为 ,点 表示的数为 ,以 点为圆心, 长为半径作圆弧与数轴交于点 ,则点 表示的数为.
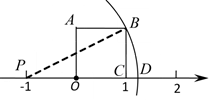 12. 在平面直角坐标系中,已知点的坐标是 , 点的坐标为 , 若为直角三角形,则的值为 .
12. 在平面直角坐标系中,已知点的坐标是 , 点的坐标为 , 若为直角三角形,则的值为 .三、解答题(本大题共5小题,每小题6分,共30分)
-
13. 计算:(1)、(2)、14. 把下列各数分别填入相应的集合中.
, , , 3.14, , 0, , .
(1)、有理数集合:{……};(2)、无理数集合:{……};(3)、正实数集合:{……}.15. 如图是的小正方形构成的网格,每个小正方形的边长为1,的三个顶点 , , 均在格点上,请仅用无刻度的直尺,在给定的网格中按要求画图,保留作图痕迹.图1
 图2
图2 (1)、三角形的面积为;(2)、在图1中画出边上高;(3)、在图2中作出的角平分线 .16. 已知 , , 求下列各式的值:(1)、;(2)、 .17. 如图,要修建一个育苗棚,棚高 , 棚宽 , 棚的长为 , 现要在矩形的棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?
(1)、三角形的面积为;(2)、在图1中画出边上高;(3)、在图2中作出的角平分线 .16. 已知 , , 求下列各式的值:(1)、;(2)、 .17. 如图,要修建一个育苗棚,棚高 , 棚宽 , 棚的长为 , 现要在矩形的棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?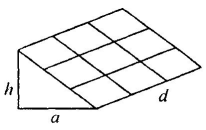
四、(本大题共3小题,每小题8分,共24分)
-
18. 某教学网站开设了有关人工智能的课程并策划了 , 两种网上学习的月收费方式:
收费方式
月使用费/元
包时上网时间/h
超时费/(元/h)
A
70
25
6
B
100
50
8
设小明每月上网学习人工智能课程的时间为 , 方案 , 的收费金额分别为元、元.
(1)、当时,分别求出 , 与之间的函数关系式;(2)、若小明3月份上该网站学习的时间为 , 则他选择哪种方式上网学习合算?19. 湖的两岸有 , 两棵景观树,数学兴趣小组设计实验测量两棵景观树之间的距离,他们在与垂直的方向上取点 , 测得米,米.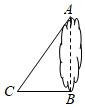 (1)、求湖的两岸 , 之间的距离;(2)、求点到直线的距离.20. 已知一次函数 . 当时,;当时, .(1)、求该一次函数的表达式;(2)、求该函数的图象与坐标轴围成的图形的面积.
(1)、求湖的两岸 , 之间的距离;(2)、求点到直线的距离.20. 已知一次函数 . 当时,;当时, .(1)、求该一次函数的表达式;(2)、求该函数的图象与坐标轴围成的图形的面积.五、(本大题共2小题,每小题9分,共18分)
-
21. 如图,每个小正方形的边长均为1.
 (1)、图中阴影部分的面积是;阴影部分正方形的边长是 .(2)、估计边长的值在两个相邻整数与之间.(3)、我们知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,用表示它的小数部分.设边长的整数部分为 , 小数部分为 , 求的值.22. 如图1,一只蚂蚁要从圆柱的下底面的点爬到上底面的点处,求它爬行的最短距离.已知圆柱底面半径为 , 高度为 . 小明同学在研究这个问题时,提出了两种可供选择的方案,方案1:沿爬行;方案2:沿圆柱侧面展开图的线段爬行,如图2.(取3)
(1)、图中阴影部分的面积是;阴影部分正方形的边长是 .(2)、估计边长的值在两个相邻整数与之间.(3)、我们知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,用表示它的小数部分.设边长的整数部分为 , 小数部分为 , 求的值.22. 如图1,一只蚂蚁要从圆柱的下底面的点爬到上底面的点处,求它爬行的最短距离.已知圆柱底面半径为 , 高度为 . 小明同学在研究这个问题时,提出了两种可供选择的方案,方案1:沿爬行;方案2:沿圆柱侧面展开图的线段爬行,如图2.(取3)图1
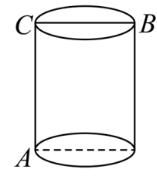 图2
图2 (1)、当 , 时,哪种方式的爬行距离更近?(2)、当 , 时,哪种方式的爬行距离更近?(3)、当与满足什么条件时,两种方式的爬行距离同样远?
(1)、当 , 时,哪种方式的爬行距离更近?(2)、当 , 时,哪种方式的爬行距离更近?(3)、当与满足什么条件时,两种方式的爬行距离同样远?六、(本大题共12分)
-
23. 已知、两地间有汽车站站,客车由地驶向站,货车由地经过站去地(客货车在、两地间沿同一条路行驶),两车同时出发,匀速行驶.货车的速度是客车速度的 . 如图是客车、货车离站的路程与行驶时间的函数关系图象.
 (1)、求货车的速度并求、两地间的路程.(2)、求客车与的函数关系式并直接写出货车与的函数关系式.(3)、求点的坐标并说出点的实际意义.(4)、出发后经过多长时间两车间路程是?
(1)、求货车的速度并求、两地间的路程.(2)、求客车与的函数关系式并直接写出货车与的函数关系式.(3)、求点的坐标并说出点的实际意义.(4)、出发后经过多长时间两车间路程是?