安徽省安庆市重点学校2023-2024学年九年级上学期月考数学试题
试卷更新日期:2024-01-09 类型:月考试卷
一、选择题(共10小题)
-
1. 已知抛物线的顶点在轴上,则的值为( )A、16 B、 C、4 D、82. 在Rt△ABC中,∠C=90°,BC=1,AC= ,那么∠B的度数是( )A、15° B、45° C、30° D、60°3. 若双曲线位于第一、三象限,则的值可以是( )A、 B、 C、 D、4. 如图,在网格中小正方形的边长均为1,△ABC的顶点都在格点上,则等于( )
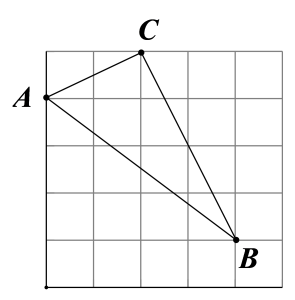 A、 B、 C、 D、5. 如图,在中,点 , 分别在边 , 上,且 , 若:=1:4,则的值为( )
A、 B、 C、 D、5. 如图,在中,点 , 分别在边 , 上,且 , 若:=1:4,则的值为( ) A、 B、 C、 D、6. 如图,在平面直角坐标系中,点在第一象限,轴于点 , 函数的图象与线段交于点 , 且.若的面积为12,则的值为( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,点在第一象限,轴于点 , 函数的图象与线段交于点 , 且.若的面积为12,则的值为( ) A、4 B、6 C、8 D、127. 某中学九年级数学兴趣小组的同学准备测量校内旗杆的高度,他们在点测得旗杆顶端的仰角 , 向前走了30米到达点,在点测得旗杆顶端A的仰角 , 则旗杆的高为多少米?( )
A、4 B、6 C、8 D、127. 某中学九年级数学兴趣小组的同学准备测量校内旗杆的高度,他们在点测得旗杆顶端的仰角 , 向前走了30米到达点,在点测得旗杆顶端A的仰角 , 则旗杆的高为多少米?( ) A、15米 B、米 C、米 D、米8. 已知二次函数的图象如图,则一次函数与反比例函数在同一平面直角坐标系中的图象大致是( )
A、15米 B、米 C、米 D、米8. 已知二次函数的图象如图,则一次函数与反比例函数在同一平面直角坐标系中的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 如图,正方形ABCD边长为8,M,N分别是边BC,CD上的两个动点,且AM⊥MN,则AN的最小值是( )
9. 如图,正方形ABCD边长为8,M,N分别是边BC,CD上的两个动点,且AM⊥MN,则AN的最小值是( )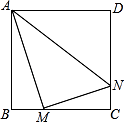 A、8 B、4 C、10 D、810. 对于二次函数 , 规定函数是它的相关函数.已知点 , 的坐标分别为 , , 连接 , 若线段与二次函数的相关函数的图象有两个公共点,则的取值范围为( )A、或 B、或 C、或 D、或
A、8 B、4 C、10 D、810. 对于二次函数 , 规定函数是它的相关函数.已知点 , 的坐标分别为 , , 连接 , 若线段与二次函数的相关函数的图象有两个公共点,则的取值范围为( )A、或 B、或 C、或 D、或二、填空题(共4小题)
-
11. 已知抛物线的对称轴为直线 , 且经过点 , , 试比较和的大小:(填“”、“”或“=”).12. 若 , 那么.13. 如图,在中, , 是的中点, , 交于 , 若 , 则.
 14. 如图,将矩形折叠,使得点落在边的三等分点上,且 , 点折叠后的对应点为 , 折痕为 , 连接 , 若 , , 则的长为.
14. 如图,将矩形折叠,使得点落在边的三等分点上,且 , 点折叠后的对应点为 , 折痕为 , 连接 , 若 , , 则的长为.
三、解答题(共6小题)
-
15. 计算:16. 如图,在平面直角坐标系中,的三个顶点坐标分别为 , , .
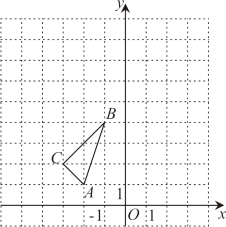 (1)、以原点O为位似中心,位似比为 , 在y轴的左侧,画出放大后的图形;(2)、直接写出点坐标 .17. 如图,已知菱形的对称中心是坐标原点 , 四个顶点都在坐标轴上,反比例函数的图象与边交于 , 两点.
(1)、以原点O为位似中心,位似比为 , 在y轴的左侧,画出放大后的图形;(2)、直接写出点坐标 .17. 如图,已知菱形的对称中心是坐标原点 , 四个顶点都在坐标轴上,反比例函数的图象与边交于 , 两点. (1)、求 , 的值;(2)、写出函数图象在菱形内的取值范围.18. 如图,图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面的倾斜角为 , 长为3米的真空管与水平线的夹角为 , 安装热水器的铁架水平横管的长度为0.9米,求安装热水器的铁架竖直管的长度.(结果精确到0.1米)(参考数据: , , , , , )
(1)、求 , 的值;(2)、写出函数图象在菱形内的取值范围.18. 如图,图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面的倾斜角为 , 长为3米的真空管与水平线的夹角为 , 安装热水器的铁架水平横管的长度为0.9米,求安装热水器的铁架竖直管的长度.(结果精确到0.1米)(参考数据: , , , , , ) 19. 李大爷每天到批发市场购进某种水果进行销售,这种水果每箱10千克,批发商规定:整箱购买,一箱起售,每人一天购买不超过10箱;当购买1箱时,批发价为8.2元/千克,每多购买1箱,批发价每千克降低0.2元.根据李大爷的销售经验,这种水果售价为12元/千克时,每天可销售1箱;售价每千克降低0.5元,每天可多销售1箱.(1)、请求出这种水果批发价(元/千克)与购进数量(箱)之间的函数关系式;(2)、若每天购进的这种水果需当天全部售完,请你计算,李大爷每天应购进这种水果多少箱,才能使每天所获利润最大?最大利润是多少?20. 如图 , 在正方形中,点是对角线上一点不与点 , 重合 , 交边于点 , 连接 , 过点作交的延长线于点 , 连接 .
19. 李大爷每天到批发市场购进某种水果进行销售,这种水果每箱10千克,批发商规定:整箱购买,一箱起售,每人一天购买不超过10箱;当购买1箱时,批发价为8.2元/千克,每多购买1箱,批发价每千克降低0.2元.根据李大爷的销售经验,这种水果售价为12元/千克时,每天可销售1箱;售价每千克降低0.5元,每天可多销售1箱.(1)、请求出这种水果批发价(元/千克)与购进数量(箱)之间的函数关系式;(2)、若每天购进的这种水果需当天全部售完,请你计算,李大爷每天应购进这种水果多少箱,才能使每天所获利润最大?最大利润是多少?20. 如图 , 在正方形中,点是对角线上一点不与点 , 重合 , 交边于点 , 连接 , 过点作交的延长线于点 , 连接 . (1)、求证:∽;(2)、求的度数;(3)、若正方形的边长为 , 点是延长线上一点,交的延长线于点 , 且恰好经过的中点,如图 , 其他条件不变,求的值.
(1)、求证:∽;(2)、求的度数;(3)、若正方形的边长为 , 点是延长线上一点,交的延长线于点 , 且恰好经过的中点,如图 , 其他条件不变,求的值.