天津市重点中学2023-2024学年九年级上学期数学学科第二次月考试卷
试卷更新日期:2024-01-09 类型:月考试卷
一、选择题:
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知中, , 若以2为半径作 , 则斜边与的位置关系是( )A、相交 B、相离 C、相切 D、无法确定3. 如图,在平面直角坐标系中,点为坐标原点,点在第一象限,与轴交于两点,点的坐标为的半径为 , 则点的坐标为( )
2. 已知中, , 若以2为半径作 , 则斜边与的位置关系是( )A、相交 B、相离 C、相切 D、无法确定3. 如图,在平面直角坐标系中,点为坐标原点,点在第一象限,与轴交于两点,点的坐标为的半径为 , 则点的坐标为( ) A、 B、 C、 D、4. 如图,在中, , 将绕点逆时针旋转得到 , 点的对应点恰好落在边上,的对应点为 . 则下列结论一定正确的是( )
A、 B、 C、 D、4. 如图,在中, , 将绕点逆时针旋转得到 , 点的对应点恰好落在边上,的对应点为 . 则下列结论一定正确的是( ) A、 B、 C、 D、5. 正六边形内接于 , 正六边形的周长是12,则正六边形内切圆的半径是( )A、 B、2 C、 D、6. 如图,已知 , 那么添加下列一个条件后,仍不能判定的是( )
A、 B、 C、 D、5. 正六边形内接于 , 正六边形的周长是12,则正六边形内切圆的半径是( )A、 B、2 C、 D、6. 如图,已知 , 那么添加下列一个条件后,仍不能判定的是( ) A、 B、 C、 D、7. 如图,若 , 垂足分别是 , 且 , 则的长是( )
A、 B、 C、 D、7. 如图,若 , 垂足分别是 , 且 , 则的长是( ) A、2 B、3 C、4.5 D、68. 如图,在边长为1的小正方形组成的网格中,四个点均在格点上,与相交于点 , 连接 , 则与的面积比是( )
A、2 B、3 C、4.5 D、68. 如图,在边长为1的小正方形组成的网格中,四个点均在格点上,与相交于点 , 连接 , 则与的面积比是( ) A、1∶4 B、4∶1 C、1∶2 D、2∶19. 如图,的斜边在轴上, , 含角的顶点与原点重合,直角顶点在第二象限,将绕点O顺时针旋转后得到 , 则点的对应点的坐标是( )
A、1∶4 B、4∶1 C、1∶2 D、2∶19. 如图,的斜边在轴上, , 含角的顶点与原点重合,直角顶点在第二象限,将绕点O顺时针旋转后得到 , 则点的对应点的坐标是( ) A、 B、 C、 D、10. 如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A、 B、 C、 D、10. 如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )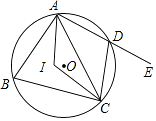 A、56° B、62° C、68° D、78°11. 已知二次函数和(是常数)的图象与轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为( )A、 B、 C、4 D、212. 如图,要围一个矩形菜园 , 共中一边是墙,且的长不能超过 , 其余的三边用篱笆,且这三边的和为 . 有下列结论:
A、56° B、62° C、68° D、78°11. 已知二次函数和(是常数)的图象与轴都有两个交点,且这四个交点中每相邻两点间的距离都相等,则这两个函数图象对称轴之间的距离为( )A、 B、 C、4 D、212. 如图,要围一个矩形菜园 , 共中一边是墙,且的长不能超过 , 其余的三边用篱笆,且这三边的和为 . 有下列结论:①的长可以为;
②的长有两个不同的值满足菜园面积为;
③菜园面积的最大值为 .
其中,正确结论的个数是( )
 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题:
-
13. 二次函数图象的顶点坐标是 .14. 不透明的袋子中装有9个球,其中有3个红球,6个绿球,这些球除颜色外无其他差别,从袋子中随机取出1个球,则它是绿球的概率是 .15. 圆锥的底面半径是 , 母线长 , 则它的侧面展开图的圆心角的度数为 .16. 如图,边长为的正方形内接于 , 分别过点A , D作的切线,两条切线交于点P , 则图中阴影部分的面积是.
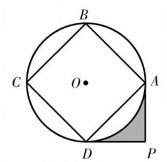 17. 如图,已知 , 点在所在直线上运动,以为边作等边三角形 , 则 . 在点运动过程中,的最小值为 .
17. 如图,已知 , 点在所在直线上运动,以为边作等边三角形 , 则 . 在点运动过程中,的最小值为 . 18. 如图,将线段放在边长为1的小正方形网格,点点均落在格点上,
18. 如图,将线段放在边长为1的小正方形网格,点点均落在格点上,
⑴的长等于 ;⑵请用无刻度直尺在线段上画出点P , 使并保留作图痕迹.

三、解答题:
-
19. 解下列方程(1)、(2)、20. 如图,已知⊙O的弦CD垂直于直径AB,点E在CD上,且EC = EB .
 (1)、求证:△CEB∽△CBD ;(2)、若CE = 3,CB=5 ,求DE的长.21. 甲、乙两位同学相约打乒乓球.用列表法或树状图法解决下列问题:(1)、有款式完全相同的4个乒乓球拍(分别记为A , B , C , D),若甲先从中随机选取1个,乙再从余下的球拍中随机选取1个,求乙选中球拍C的概率;(2)、双方约定:两人各投掷一枚质地均匀的硬币,如果两枚硬币全部正面向上或全部反面向上,那么甲先发球,否则乙先发球.这个约定是否公平?为什么?22. 已知在中,弦与直径交于点 .
(1)、求证:△CEB∽△CBD ;(2)、若CE = 3,CB=5 ,求DE的长.21. 甲、乙两位同学相约打乒乓球.用列表法或树状图法解决下列问题:(1)、有款式完全相同的4个乒乓球拍(分别记为A , B , C , D),若甲先从中随机选取1个,乙再从余下的球拍中随机选取1个,求乙选中球拍C的概率;(2)、双方约定:两人各投掷一枚质地均匀的硬币,如果两枚硬币全部正面向上或全部反面向上,那么甲先发球,否则乙先发球.这个约定是否公平?为什么?22. 已知在中,弦与直径交于点 . (1)、如图①,若 , 求的度数.(2)、如图②,过点作的切线交的延长线于点 . 若 , 求的度数.23. 在一次足球训练中,小明从球门正前方的A处射门,球射向球门的路线呈抛物线,球飞行的水平距离为时,球达到最高点,此时球离地面 , 已知球门高OB为 , 以O为原点,建立如图所示直角坐标系.
(1)、如图①,若 , 求的度数.(2)、如图②,过点作的切线交的延长线于点 . 若 , 求的度数.23. 在一次足球训练中,小明从球门正前方的A处射门,球射向球门的路线呈抛物线,球飞行的水平距离为时,球达到最高点,此时球离地面 , 已知球门高OB为 , 以O为原点,建立如图所示直角坐标系. (1)、求抛物线的表达式;(2)、通过计算判断球能否进球门;(3)、若抛物线的形状、最大高度均保持不变,且抛物线恰好经过点O正上方处,则该抛物线应向右平移几个单位?24. 如图,在矩形中, , 以点为中心将矩形旋转任意角度,得到矩形 , 点的对应点分别为 .
(1)、求抛物线的表达式;(2)、通过计算判断球能否进球门;(3)、若抛物线的形状、最大高度均保持不变,且抛物线恰好经过点O正上方处,则该抛物线应向右平移几个单位?24. 如图,在矩形中, , 以点为中心将矩形旋转任意角度,得到矩形 , 点的对应点分别为 . (1)、如图①,当点落在边上时,求线段的长;(2)、如图②,当点落在线段上时,与交于点 , 求线段的长;(3)、如图③,若矩形的对角线相交于点 , 连接 , 若面积为请直接写出的取值范围 .25. 已知抛物线与轴交于点 , 与轴交于点 , 连接 , 点为此抛物线的顶点.(1)、求抛物线的解析式;(2)、抛物线上两点之间的距离是;(3)、①:点是第一象限内抛物线上的动点,连接和 , 求面积的最大值;
(1)、如图①,当点落在边上时,求线段的长;(2)、如图②,当点落在线段上时,与交于点 , 求线段的长;(3)、如图③,若矩形的对角线相交于点 , 连接 , 若面积为请直接写出的取值范围 .25. 已知抛物线与轴交于点 , 与轴交于点 , 连接 , 点为此抛物线的顶点.(1)、求抛物线的解析式;(2)、抛物线上两点之间的距离是;(3)、①:点是第一象限内抛物线上的动点,连接和 , 求面积的最大值;②:在①的条件下,当的面积最大时,为轴上一点,过点作抛物线对称轴的垂线,垂足为 , 连接 , 探究是否存在最小值.若存在,请直接写出此时点的坐标;若不存在,请说明理由.