安徽省安庆市重点学校2023-2024学年七年级上学期月考数学试题

试卷更新日期：2024-01-09 类型：月考试卷

进入出卷网下载

一、选择题

1. 截止10月7日早上，杭州亚运会赛事门票销售超305万张，票务收入超过6.1亿元，将6.1亿用科学记数法表示应为（）

A、 $0.61 \times 1 0^{9}$ B、 $6.1 \times 1 0^{8}$ C、 $6.1 \times 1 0^{9}$ D、 $61 \times 1 0^{7}$

查看试题解析
2. 下列变形中，不正确的是（）

A、若 $x = y$ ，则 $x + 3 = y + 3$ B、若 $- 2 x = - 2 y$ ，则 $x = y$ C、若 $\frac{x}{m} = \frac{y}{m}$ ，则 $x = y$ D、若 $x = y$ ，则 $\frac{x}{m} = \frac{y}{m}$

查看试题解析
3. 下列说法正确的是（）

A、单项式 $- a$ 的系数是1 B、 $4 a + b - 1$ 的各项分别为 $4 a$ ， b ， 1 C、单项式 $- 2 a b c^{2}$ 的次数是3 D、 $5 a^{2} b^{3} - 4 a^{2} b + 1$ 是五次三项式

查看试题解析
4. 由 $x + 2 y = 1$ 可以得到用 $x$ 表示 $y$ 的式子为（）

A、 $x = - 2 y + 1$ B、 $x = - 2 y - 1$ C、 $y = \frac{x}{2} + \frac{1}{2}$ D、 $y = - \frac{x}{2} + \frac{1}{2}$

查看试题解析
5. 下列各选项中正确的是（）

A、由 $7 x = 4 x - 3$ 移项得 $7 x - 4 x = 3$ B、由 $2 (x + 1) = x + 7$ 移项、合并同类项得 $x = 3$ C、由 $2 (2 x - 1) - 3 (x - 3) = 1$ 去括号得 $4 x - 2 - 3 x - 9 = 1$ D、由 $\frac{2 x - 1}{3} = 1 + \frac{x - 3}{2}$ 去分母得 $2 (2 x - 1) = 6 + 3 (x - 3)$

查看试题解析
6. 已知关于 $x$ 的方程 $m x - 4 = 3 x + m$ 的解是 $x = 2$ ，则 $m$ 的值是（）

A、2 B、 $- 2$ C、10 D、 $- 10$

查看试题解析
7. 若方程组 ${\begin{array}{l} x + y = a - 1 ， \\ x + 2 y = 4 \end{array}$ 的解也是二元一次方程 $x - y = 1$ 的一个解，则 $a$ 的值为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 某同学在解方程 $5 x - 1 = () x + 3$ 时，把“（）”处的数看成了它的相反数，解得 $x = 2$ ，则该方程的正确解应为（）

A、 $x = - \frac{1}{2}$ B、 $x = \frac{1}{2}$ C、 $x = 2$ D、 $x = 1$

查看试题解析
9. 如图，把四张大小相同的长方形卡片（如图①）按图②、图③两种方式放在一个底面为长方形（长比宽多 $3 c m$ ）的盒底上，底面未被卡片覆盖的部分用阴影表示，若记图②中阴影部分的周长为 $C_{1}$ ，图③中阴影部分的周长为 $C_{2}$ ，那么 $G_{1}$ 比 $C_{2}$ 大（） $c m$ .

A、6 B、9 C、10 D、12

查看试题解析
10. 幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中，要求每一横行、每一数列以及两条对角线上的3个数之和相等，例如图（1）就是一个幻方.图（2）是一个未完成的幻方，则 $x$ 与 $y$ 的和是（）
图（1）
4
9
2
3
5
7
8
1
6
图（2）
x
6
20
22

y

A、9 B、10 C、11 D、12

查看试题解析

二、填空题

11. 若代数式 $x + 1$ 与 $2 x - 7$ 的值是互为相反数，则 $x$ 的值为.

查看试题解析
12. 单项式 $6 x^{5} y^{2 n}$ 与 $- 2 x^{m} y^{4}$ 的和仍是单项式，则 $m + n =$ .

查看试题解析
13. 某商场促销，把原价2500元的空调以八折出售，仍可获利400元，则这款空调进价为元.

查看试题解析
14. 已知关于x ， y的二元一次方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} ， \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解为 ${\begin{array}{l} x = 3 ， \\ y = 4 ， \end{array}$ 则关于x ， y的方程组 ${\begin{array}{l} 3 a_{1} x - b_{1} y = c_{1} \\ 3 a_{2} x - b_{2} y = c_{2} \end{array}$ 的解为.

查看试题解析
15. 已知长为300米的秋游队伍，以2米/秒的速度向东行进，在队尾处的甲有一物品要送到队头，送到后立即返回队尾.若甲的往返速度均为4米/秒，则甲往返共用的时间为秒.

查看试题解析

三、解答题

16.

(1)、计算 $- 2^{2} + (- 1)^{3} \times 5 - (- 27) \div 9$

(2)、化简 $- 2 (2 x^{2} - x + 4) + 3 (x^{2} - 2 x + 3)$

查看试题解析
17. 解方程（组）

(1)、 $\frac{5 y + 4}{3} + \frac{y - 1}{4} = 2 - \frac{5 y - 5}{12}$

(2)、 ${\begin{array}{l} 9 x + 8 y = - 2 \\ 4 x + 5 y = - 11 \end{array}$

查看试题解析
18. 在解方程组 ${\begin{array}{l} a x + b y = 16 ① \\ b x + a y = 19 ② \end{array}$ 时，小明把方程①抄错了，从而得到解为 ${\begin{array}{l} x = 1 \\ y = 7 \end{array}$ ，而小亮却把方程②抄错了，得到解为 ${\begin{array}{l} x = - 2 \\ y = 4 \end{array}$ ，求a ， b的值.

查看试题解析
19. 为了更好的落实国家“双减”政策，增强学生体质，某中学利用课后服务时间开设了花样跳绳社团兴趣小组.学校用1000元从体育用品商店购入A、B两种款式的跳绳各40条，且购买的 $B$ 种跳绳的单价比 $A$ 种跳绳单价的2倍还少5元，求购买A、B两种款式跳绳的单价各是多少元？

查看试题解析
20. 安庆吾悦广场某影厅共有16排座位，第1排有m个座位，第2排比第1排多6个座位，第3排及后面每排座位数相同，都比第2排多n个座位.

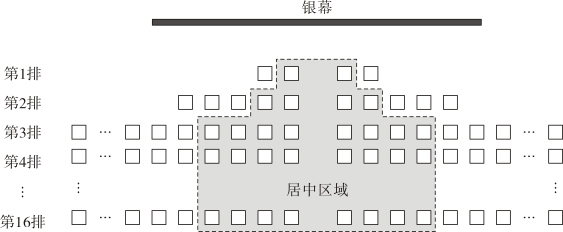(1)、该影厅第3排有个座位（用含m ， n的式子表示）；

(2)、图中的阴影区域为居中区域，第1排的两侧各去掉1个座位后得到第1排的居中区域，第2排的居中区域比第1排的居中区域在两侧各多1个座位，第3排及后面每排的居中区域座位数相等，都比第2排的居中区域在两侧各多2个座位.居中区域的第7，8，9排为最佳观影位置.
①若该影厅的第1排有11个座位，则居中区域的第2排有 ▲ 个座位，居中区域的第3排有 ▲ 个座位；
②若该影厅的最佳观影位置共有39个座位，求该影厅共有多少个座位？（用含n的式子表示）.

查看试题解析
21. 如图1，已知甲、乙两个圆柱形量筒（量筒厚度忽略不计）的底面半径分别为 $10 c m$ 和 $5 c m$ ，高均为 $24 c m$ ，并都装有一定量的水，甲的水位高 $12 c m$ ，乙的水位高 $h c m$ .现从甲倒一部分水到乙，甲的水位降低 $x c m$ .（圆周率用 $π$ 表示）

(1)、乙的水位增加 $c m$ （用含x的代数式表示）；

(2)、若 $h = 2 c m$ ，倒水后甲、乙的水位高度相等，则倒水后甲的水位高多少 $c m$ ？

(3)、如图2，倒水后将乙放入甲的底部.当倒入乙的水使乙的水位增加一倍时，乙放入甲之后；两量筒内的水位高度恰好相等，求x的值.

查看试题解析