人教版初中数学2023-2024学年八年级下学期课时培优练习 17.2勾股定理逆定理

试卷更新日期：2024-01-09 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在平面直角坐标系中，点 $A (- 2 ， 2)$ ， $B (2 ， 1)$ ，点 $P (x ， 0)$ 是 $x$ 轴上的一个动点．结合图形得出式子 $\sqrt{(x + 2)^{2} + 4} + \sqrt{(2 - x)^{2} + 1}$ 的最小值是（）

A、3 B、 $\sqrt{17}$ C、5 D、 $2 \sqrt{2} + \sqrt{5}$

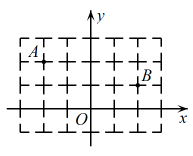查看试题解析
2. 如图，在墙角处放着一个长方体木柜（木柜与墙面和地面均没有缝腺），一只蚂蚁从柜角 $A$ 处沿着木柜表面爬到柜角 $C_{1}$ 处．若 $A B = 3$ ， $B C = 4$ ， $C C_{1} = 5$ ，则蚂蚁爬行的最短路程是（）

A、 $\sqrt{74}$ B、 $3 \sqrt{10}$ C、 $\sqrt{89}$ D、12

查看试题解析
3. 在边长为12的正方形ABCD中，E为CD边中点，连接AE，将 $△ A D E$ 沿线段AE翻折得到 $△ A F E$ ，延长AF交BC边于点N，连接EN，延长EF交BC边于点G，其中 $B G = 4$ ，连接DF并延长交BC边于点K，连接EK，则下列结论：① $D F ⊥ A E$ ；② $△ E C N ≌ △ E F N$ ；③ $∠ E K C = 45 °$ ；④ $A N = 4 \sqrt{13}$ ；⑤ $S_{△ G K E} = S_{△ G F N}$ ．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 勾股定理是人类最伟大的科学发现之一，在我国古代算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大的正方形内．若知道图中阴影部分的面积，则一定能求出（）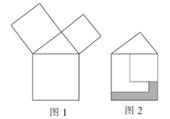

A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和

查看试题解析
5.
如图是一块长、宽、高分别为6cm、4cm、3cm的长方体木块，一只蚂蚁要从长方体木块的一个顶点A处，沿着长方体的表面到长方体上和A相对的顶点B处吃食物，那么它需要爬行的最短路径的长是（）

A、 $(3 + 2 \sqrt{13})$ cm B、 $\sqrt{97}$ cm C、 $\sqrt{85}$ cm D、9cm

查看试题解析
6. 一艘轮船以16海里∕小时的速度从港口A出发向东北方向航行，同时另一轮船以12海里∕小时从港口A出发向东南方向航行，离开港口3小时后，则两船相距（　　）

A、36海里 B、48海里 C、60海里 D、84海里

查看试题解析
7. 下列命题：
①如果a、b、c为一组勾股数，那么4a、4b、4c仍是勾股数；
②如果直角三角形的两边是3，4，那么斜边必是5；
③如果一个三角形的三边是12，25，21，那么此三角形必是直角三角形；
④一个等腰直角三角形的三边是a、b、c，（a＞b=c），那么a²：b²：c²=2：1：1．
其中正确的是（　　）

A、①② B、①③ C、①④ D、②④

查看试题解析
8. 如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（）

A、12≤a≤13 B、12≤a≤15 C、5≤a≤12 D、5≤a≤13

查看试题解析
9.
如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米．一只鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行（）

A、8米 B、10米 C、12米 D、14米

查看试题解析
10.
如图，是一个三级台阶，它的每一级的长、宽、高分别为20dm、3dm、2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点的最短路程是（）

A、20 $\sqrt{3}$ B、25 $\sqrt{2}$ C、20 D、25

查看试题解析

二、填空题

11. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 4$ ，分别以 $A C$ ， $B C$ 为直径向外作半圆，半圆的面积分别记为 $S_{1}$ ， $S_{2}$ ，则 $S_{1} + S_{2}$ 的值为

查看试题解析
12. 如图，在正方形 $A B C D$ 中， $A B = 3$ ， M是 $A D$ 边上的一点，连接 $B M$ ， $A M = 1$ ．将 $△ B M A$ 沿 $B M$ 对折至 $△ B M N$ ，连接 $D N$ ，则 $D N$ 的长是．

查看试题解析
13.
如图，正方形ABCD，AC、BD交于点O，点E、F分别在AB、BC上，且∠EOF=90°，则下列结论①AE=BF，②OE=OF，③BE+BF=AD，④AE²+CF²=2OE²中正确的有（只写序号）

查看试题解析
14. 在我国古代数学著作《九章算术》中记载了一道有趣的数学问题：“今有池方一丈，葭生其中央，出水一尺．引葭赴岸，适与岸齐．问水深、葭长备几何？”这个数学问题的意思是说：“有一个水池，水面是一个边长为 $1$ 丈（ $1$ 丈 $= 10$ 尺）的正方形，在水池正中央长有一根芦苇，芦苇露出水面 $1$ 尺．如果把这根芦苇拉向岸边，它的顶端恰好到达岸边的水面．请问这个水池的深度和这根芦苇的长度各是多少？”设这个水池的深度是 $x$ 尺，根据题意，可列方程为．

查看试题解析
15. 如图，长方体纸箱的长、宽、高分别为50cm、30cm、60cm，一只蚂蚁从点A处沿着纸箱的表面爬到点B处.蚂蚁爬行的最短路程为cm.

查看试题解析

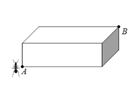
三、解答题

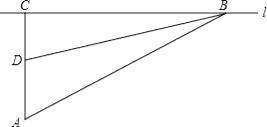
16. 校车安全是近几年社会关注的热点问题，安全隐患主要是超速和超载．某中学九年级数学活动小组进行了测试汽车速度的实验，如图，先在笔直的公路l旁选取一点A，在公路l上确定点B、C，使得AC⊥l，∠BAC=60°，再在AC上确定点D，使得∠BDC=75°，测得AD=40米，已知本路段对校车限速是50千米/时，若测得某校车从B到C匀速行驶用时10秒，问这辆车在本路段是否超速？请说明理由（参考数据： $\sqrt{2}$ =1.41， $\sqrt{3}$ =1.73）

查看试题解析
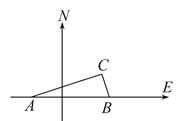
17.
如图，在我国沿海有一艘不明国籍的轮船进入我国海域，我海军甲、乙两艘巡逻艇立即从相距13nmile的A，B两个基地前去拦截，六分钟后同时到达C地将其拦截．已知甲巡逻艇每小时航行120nmile，乙巡逻艇每小时航行50nmile，航向为北偏西40°，问：甲巡逻艇的航向是多少？

查看试题解析
18. 如图所示，一个梯子 $A B$ 长2.5米，顶端 $A$ 靠墙 $A C$ 上，这时梯子下端 $B$ 与墙角 $C$ 的距离为1.5米，梯子滑动后停在 $D E$ 上的位置上，如图，测得 $D B$ 的长0.5米，求梯子顶端 $A$ 下落了多少米？

查看试题解析

四、综合题

19. 我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法，其实分解因式的方法还有分组分解法、添项拆项法、十字相乘法等等．①分组分解法：将一个多项式适当分组后，可提公因式或运用公式继续分解的方法叫作分组分解法．
例如： $4 x^{2} - 4 x - y^{2} + 1 = (4 x^{2} - 4 x + 1) - y^{2} = {(2 x - 1)}^{2} - y^{2} = (2 x - y - 1) (2 x + y - 1)$

②十字相乘法：十字相乘法能用于二次三项式的分解因式．

分解步骤：1．分解二次项，所得结果分别写在十字交叉线的左上角和左下角；2．分解常数项，所得结果分别写在十字交叉线的右上角和右下角；3．交叉相乘，求代数和，使其等于一次项；4．观察得出原二次三项式的两个因式，并表示出分解结果．这种分解方法叫作十字相乘法．

例如： $x^{2} - 3 x - 40$ 分析： $x^{2} - 3 x - 40$

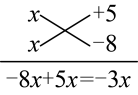
观察得出：两个因式分别为 $(x + 5)$ 与 $(x - 8)$

解：原式 $= (x + 5) (x - 8)$

③添项拆项法：将一个多项式的某一项拆成两项后，可提公因式或运用公式继续分解的方法叫作拆项法．

例如： $y^{2} - 10 y + 21 = y^{2} - 10 y + 25 - 4 = {(y - 5)}^{2} - 2^{2} = (y - 5 + 2) (y - 5 - 2) = (y - 3) (y - 7)$ ．

(1)、仿照以上方法，按照要求分解因式：
①（分组分解法） $a b - a - b + 1 =$ ；
②（十字相乘法） $y^{2} + 3 y - 10 =$ ；

(2)、已知：a、b、c为 $△ A B C$ 的三条边， $a^{2} + b^{2} + c^{2} - 6 a = 10 b + 8 c - 50$ ，判断 $△ A B C$ 的形状．

查看试题解析
20. 请完成下列题目：

(1)、
如图①所示，P是等边△ABC内的一点，连接PA、PB、PC，将△BAP绕B点顺时针旋转60°得△BCQ，连接PQ．若PA2+PB2=PC2，证明∠PQC=90°.

(2)、
如图②所示，P是等腰直角△ABC（∠ABC=90°）内的一点，连接PA、PB、PC，将△BAP绕B点顺时针旋转90°得△BCQ，连接PQ．当PA、PB、PC满足什么条件时，∠PQC=90°？请说明

查看试题解析