人教版初中数学2023-2024学年八年级下学期课时基础练习 17.2勾股定理逆定理

试卷更新日期：2024-01-09 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在正方形网格中，每个小正方形的边长都是1， $A B 、 C D 、 E F 、 G H$ 四条线段，其中能组成直角三角形三边的一组线段是（）

A、 $A B 、 C D 、 G H$ B、 $A B 、 C D 、 E F$ C、 $A B 、 E F 、 G H$ D、 $C D 、 E F 、 G H$

查看试题解析
2. 下列几组数中，不能作为直角三角形的三边长的是（）

A、2，3，4 B、3，4，5 C、6，8，10 D、9，12，15

查看试题解析
3. 如果梯子的底端离建筑物1.5米，2.5米长的梯子可以达到建筑物的高度是（）

A、2米 B、2.5米 C、3米 D、3. 5米

查看试题解析
4. 满足下列条件的 $△ A B C$ ，不是直角三角形的为（）

A、 $∠ A ： ∠ B ： ∠ C = 5 ： 12 ： 13$ B、 $∠ A = ∠ B - ∠ C$ C、 $b^{2} = a^{2} - c^{2}$ D、 $a ： b ： c = 3 ： 5 ： 4$

查看试题解析
5. 下列图各组数中，是勾股数的是（）

A、6，8，12 B、0.6，0.8，1 C、8，15，16 D、9，12，15

查看试题解析
6. 如图，一只蚂蚁绕着圆柱向上螺旋式爬行，假设蚂蚁绕圆柱外壁从点A爬到点B ，圆周率π取近似值3，则蚂蚁爬行路线的最短路径长为（　　）

A、6 $\sqrt{2}$ cm B、6 $\sqrt{5}$ cm C、2 $\sqrt{13}$ cm D、10cm

查看试题解析
7. 如图，在长方体 $A B C D - E F G H$ 盒子中， $A B = 4 c m$ ， $B C = 3 c m$ ， $C G = 5 c m$ ，长为10cm的细直木棒IJ恰好从小孔G处插入，木棒的一端I与底面ABCD接触.当木棒的端点I在长方形ABCD内及边界运动时，GJ长度的最小值为（）

A、 $(10 - 5 \sqrt{2}) c m$ B、3cm C、 $(10 - 4 \sqrt{2}) c m$ D、5cm

查看试题解析
8. 如图，在△ABC中， $∠ B A C = 90 °$ ， $B C = 6$ ，以AB，AC为边作正方形，这两个正方形的面积和为（）

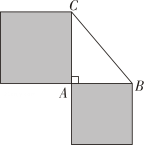A、6 B、36 C、16 D、49

查看试题解析
9. 在△ABC中，∠A ， ∠B ， ∠C的对边分别记为a ， b ， c ，根据以下条件：①∠A+∠B＝∠C；②a：b：c＝3：4：5；③a²＝c²﹣b²；④∠A：∠B：∠C＝1：2：3；⑤a＝3² ， b＝4² ， c＝5²； ⑥a＝ $\frac{1}{3}$ ， b＝ $\frac{1}{4}$ ， c＝ $\frac{1}{5}$ ．能判定△ABC为直角三角形的有（　　）

A、①②③⑤ B、②③④⑤ C、①②③④ D、①②③④⑤⑥

查看试题解析
10. 如图，点O为数轴的原点，点A和B分别对应的实数是-1和1．过点B作BC⊥AB，以点B为圆心，OB长为半径画弧，交BC于点D；以点A为圆心，AD长为半径画弧，交数轴的正半轴于点E，则点E对应的实数是（）

A、 $\sqrt{5}$ -1 B、 $\sqrt{5}$ C、 $\sqrt{3}$ D、 $\sqrt{3}$ -1

查看试题解析

二、填空题

11. 如图，长方体的底面边长分别为 $3 c m$ 和 $3 c m$ ，高为 $5 c m$ ，如果一只蚂蚁从点 $P$ 开始经过四个侧面爬行一圈到达点 $Q$ ，那么蚂蚁爬行的最短路径长为 $c m$ ．

查看试题解析
12. 如图，在高 $B C = 3 m$ ，斜坡长 $A B = 5 m$ ，宽为2m的楼梯表面铺地毯，则地毯的面积至少需要 $m^{2}$ .

查看试题解析
13. 如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，连接AB、BC ，则∠ABC的度数为．

查看试题解析
14. 如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB=∠B=30°，OA=2，将△AOB绕点O逆时针旋转90°，点B的对应点B'的坐标是

查看试题解析
15. 如图，圆柱形玻璃杯，底面周长为16cm ， AC是底面圆的直径，点P是BC上的一点，且BC＝20cm ， $P C = \frac{3}{4} B C$ ，一只蚂蚁从点A出发，沿着圆柱体的表面爬行到点P的最短距离为 cm ．

查看试题解析

三、解答题

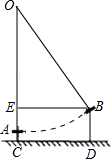
16. 《西江月》中描述：平地秋千未起，踏板一尺离地，送行二步恰竿齐，五尺板高离地…；翻译成现代文为：如图，秋千 $O A$ 静止的时候，踏板离地高一尺（ $A C = 1$ 尺）将它往前推进两步（ $E B = 10$ 尺），此时踏板升高离地五尺（ $B D = 5$ 尺），求秋千绳索 $O B$ 的长度．

查看试题解析
17. 在 $△ A B C$ 中， $∠ A 、 ∠ B 、 ∠ C$ 的对边分别用 $a 、 b 、 c$ 来表示，且 $a 、 b 、 c$ 满足 ${(a - 6)}^{2} + | b - 8 | + | c - 10 |^{2} = 0$ ，试判断 $△ A B C$ 的形状．

查看试题解析
18. 如图，A、B两个村在河流CD的同侧，分别到河的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A、B俩村供水，铺设水管的费用为每千米1万，请你在河流CD上选择水厂的位置P，使铺设水管的费用最节省，并求出总费用是多少？

查看试题解析
19. 如图，一架25m长的梯子（AC）斜靠在与地面（OA）垂直的墙（OC）上，梯子底端离墙7m.

(1)、这架梯子的顶端距离地面有多高？

(2)、如果梯子的顶端下滑了4m，那么梯子的底端在水平方向滑动了多少米？

查看试题解析
20. 校园内有一处池塘，数学实践小组的同学想利用所学知识测量池塘两端 $A$ ， $B$ 两点之间的距离，他们的操作过程如下：①沿 $A B$ 延长线的方向，在池塘边的空地上选点 $C$ ，使 $B C = 6$ 米；②在 $A C$ 的一侧选点 $D$ ，恰好使 $B D = 8$ 米， $C D = 10$ 米；③测得 $A D = 17$ 米.请根据他们的操作过程，求出 $A$ ， $B$ 两点间的距离.

查看试题解析