人教版初中数学2023-2024学年八年级下学期课时培优练习 17.1勾股定理
试卷更新日期:2024-01-09 类型:同步测试
一、选择题
-
1. 我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为 , , . 若 , 则下列关于 , , 的说法正确的是( )
 A、 B、 C、 D、2. 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,以点A为圆心,适当长为半径画弧,分别交AC , AB于点M , N , 再分别以M , N为圆心,大于的长为半径画弧,两弧在∠CAB的内部相交于点P , 画射线AP与BC交于点D , DE⊥AB , 垂足为E . 则下列结论错误的是( )
A、 B、 C、 D、2. 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,以点A为圆心,适当长为半径画弧,分别交AC , AB于点M , N , 再分别以M , N为圆心,大于的长为半径画弧,两弧在∠CAB的内部相交于点P , 画射线AP与BC交于点D , DE⊥AB , 垂足为E . 则下列结论错误的是( )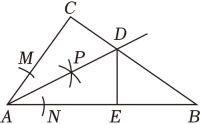 A、∠CAD=∠BAD B、CD=DE C、 D、3. 如图,在中,边的垂直平分线分别交 , 于点 , , 边的垂直平分线分别交 , BC于点N , F , 的周长为9.若 , , 则的面积为( )
A、∠CAD=∠BAD B、CD=DE C、 D、3. 如图,在中,边的垂直平分线分别交 , 于点 , , 边的垂直平分线分别交 , BC于点N , F , 的周长为9.若 , , 则的面积为( ) A、 B、 C、5 D、4. 如图,在矩形中,以点为圆心,的长为半径画弧,交于点 , 再分别以点 , 为圆心,大于的长为半径画弧,两弧交于点 , 作射线交于点若 , , 则长为( )
A、 B、 C、5 D、4. 如图,在矩形中,以点为圆心,的长为半径画弧,交于点 , 再分别以点 , 为圆心,大于的长为半径画弧,两弧交于点 , 作射线交于点若 , , 则长为( ) A、 B、 C、 D、5. 如图,圆柱底面半径为 , 高为 , 点、分别是圆柱两底面圆周上的点,且、在同一母线上,用一根棉线从点顺着圆柱侧面绕圈到点,则这根棉线的长度最短为( )
A、 B、 C、 D、5. 如图,圆柱底面半径为 , 高为 , 点、分别是圆柱两底面圆周上的点,且、在同一母线上,用一根棉线从点顺着圆柱侧面绕圈到点,则这根棉线的长度最短为( ) A、 B、 C、 D、6. 如图,在正方形中,点在上,点在的延长线上满足 , 连接 , 取的中点 , 连接 , , 若 , 则( )
A、 B、 C、 D、6. 如图,在正方形中,点在上,点在的延长线上满足 , 连接 , 取的中点 , 连接 , , 若 , 则( ) A、 B、 C、 D、7. 如图,在矩形中, , 为的中点,连接 , 将沿所在直线翻折至四边形所在平面内,得 , 延长与交于点 , 若 , 则四边形的面积为( )
A、 B、 C、 D、7. 如图,在矩形中, , 为的中点,连接 , 将沿所在直线翻折至四边形所在平面内,得 , 延长与交于点 , 若 , 则四边形的面积为( )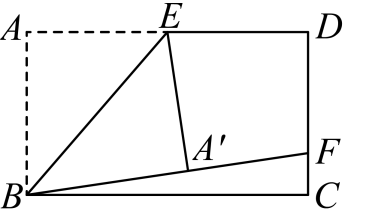 A、 B、8 C、12 D、168. 如图,中, , , . 以 , 为直角边,构造;再以 , 为直角边,构造;……,按照这个规律,在中,点到的距离是( )
A、 B、8 C、12 D、168. 如图,中, , , . 以 , 为直角边,构造;再以 , 为直角边,构造;……,按照这个规律,在中,点到的距离是( )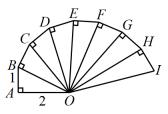 A、 B、 C、 D、9. 如图,在等边中,于D,延长到E,使 , F是的中点,连接并延长交于G,的垂直平分线分别交于点M,点N,连接 , , 下列结论:①;②;③;④ . 其中正确的结论序号是( ).
A、 B、 C、 D、9. 如图,在等边中,于D,延长到E,使 , F是的中点,连接并延长交于G,的垂直平分线分别交于点M,点N,连接 , , 下列结论:①;②;③;④ . 其中正确的结论序号是( ). A、①②③ B、②③④ C、①③④ D、①②③④10. 如图,在正方形中,点分别在上, , 与相交于点 . 下列结论:①垂直平分;②当时,为等边三角形;③当时,;④当时, . 其中正确的结论有( )个.
A、①②③ B、②③④ C、①③④ D、①②③④10. 如图,在正方形中,点分别在上, , 与相交于点 . 下列结论:①垂直平分;②当时,为等边三角形;③当时,;④当时, . 其中正确的结论有( )个. A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,△ABC中,∠A=90°,角平分线BD、CE交于点I,IF⊥CE交CA于F,下列结论:①∠DIF=45°;②CF
+BE=BC;③若AB=3,AC=4,则.其中正确的是 . 12. 如图,在△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A旋转,使点C落在AB边上的点E处,点B落在点D处,连接BD,CE,延长CE交BD于点F,则EF的长为
12. 如图,在△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A旋转,使点C落在AB边上的点E处,点B落在点D处,连接BD,CE,延长CE交BD于点F,则EF的长为
 13. 在直线上依次摆着七个正方形(如图),已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积是 , , , , 则 .
13. 在直线上依次摆着七个正方形(如图),已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积是 , , , , 则 .
 14. 如图,点、、在同一条线上,点在点 , 之间,点 , 在直线同侧, , , ≌ , 连接 , 设 , , , 下面三个结论:;;;正确的序号是 .
14. 如图,点、、在同一条线上,点在点 , 之间,点 , 在直线同侧, , , ≌ , 连接 , 设 , , , 下面三个结论:;;;正确的序号是 . 15. 如图,四边形ABCD中,AC、BD是对角线,是等边三角形,∠ADC=30°,AD=4,BD=5,则CD的长为 .
15. 如图,四边形ABCD中,AC、BD是对角线,是等边三角形,∠ADC=30°,AD=4,BD=5,则CD的长为 .
三、解答题
-
16. 如图1,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D且∠ACF=∠CBE,CG平分∠ACB交BD于点G.
 (1)、求证:△ACF≌△CBG;(2)、如图2,延长CG交AB于H,连接AG交CF于点M,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)、在(2)问的条件下,当∠FCH=2∠GAC时,若BG=4,求AM的长.17. 如图,AO⊥OM , OA=4cm,点B从O点出发沿射线OM运动,速度为1cm/s,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE.
(1)、求证:△ACF≌△CBG;(2)、如图2,延长CG交AB于H,连接AG交CF于点M,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;(3)、在(2)问的条件下,当∠FCH=2∠GAC时,若BG=4,求AM的长.17. 如图,AO⊥OM , OA=4cm,点B从O点出发沿射线OM运动,速度为1cm/s,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE. (1)、当t=3s时,
(1)、当t=3s时,①求AB的长;
②连接AF,求AF的长。
(2)、连接EF交OM于P点,当点B在射线OM上移动时,PB的长度会变化吗?若会变化,请说明理由;若不变,请求出PB的长度.18. 如图,△ABC中,BA=BC,CO⊥AB于点O,AO=4,BO=6. (1)、求BC,AC的长;(2)、若点D是射线OB上的一个动点,作DE⊥AC于点E,连结OE.
(1)、求BC,AC的长;(2)、若点D是射线OB上的一个动点,作DE⊥AC于点E,连结OE.①当点D在线段OB上时,若△AOE是以AO为腰的等腰三角形,请求出所有符合条件的OD的长.
②设DE交直线BC于点F,连结OF,若S△OBF:S△OCF=1:4,则BD的长为 ▲(直接写出所有结果).

