人教版初中数学2023-2024学年八年级下学期课时基础练习 17.1勾股定理
试卷更新日期:2024-01-09 类型:同步测试
一、选择题
-
1. 若直角三角形两条直角边的边长分别为 cm和 cm,那么此直角三角形斜边长是( )A、3 cm B、3 cm C、9cm D、27cm2. 点到原点的距离为( )A、 B、 C、 D、3. “赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为 , 较短直角边长为 , 若 , 大正方形的面积为 , 则小正方形的面积为( )
 A、 B、 C、 D、4. 如图,以原点为圆心,长为半径画弧与数轴交于点 , 若点表示的数为 , 则的值为( )
A、 B、 C、 D、4. 如图,以原点为圆心,长为半径画弧与数轴交于点 , 若点表示的数为 , 则的值为( ) A、 B、 C、 D、5. 如图,一棵大树被大风刮断后,折断处离地面8m,树的顶端离树根6m,则这棵树在折断之前的高度是( )
A、 B、 C、 D、5. 如图,一棵大树被大风刮断后,折断处离地面8m,树的顶端离树根6m,则这棵树在折断之前的高度是( )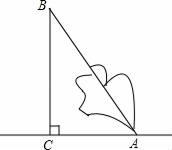 A、18m B、10m C、14m D、24m6. 如图,在中, , , , 是的垂直平分线,交于点 , 交于点 , 连接 , 则的长为( )
A、18m B、10m C、14m D、24m6. 如图,在中, , , , 是的垂直平分线,交于点 , 交于点 , 连接 , 则的长为( )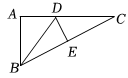 A、 B、 C、 D、7. 明朝数学家程大位在他的著作算法统宗中写了一首计算秋千绳索长度的词西江月:“平地秋千未起,踏板一尺离地送行二步恰竿齐,五尺板高离地”翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺尺 , 将它往前推进两步尺,两步尺 , 此时踏板升高离地五尺尺 , 若绳索始终拉直,则秋千绳索的长是( )
A、 B、 C、 D、7. 明朝数学家程大位在他的著作算法统宗中写了一首计算秋千绳索长度的词西江月:“平地秋千未起,踏板一尺离地送行二步恰竿齐,五尺板高离地”翻译成现代文为:如图,秋千静止的时候,踏板离地高一尺尺 , 将它往前推进两步尺,两步尺 , 此时踏板升高离地五尺尺 , 若绳索始终拉直,则秋千绳索的长是( )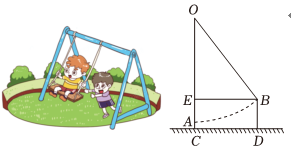 A、尺 B、尺 C、尺 D、尺8. 如图所示的是由一个直角三角形和三个正方形组成的图形,若其中 , , 则正方形的面积是( )
A、尺 B、尺 C、尺 D、尺8. 如图所示的是由一个直角三角形和三个正方形组成的图形,若其中 , , 则正方形的面积是( ) A、 B、 C、 D、9. 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )
A、 B、 C、 D、9. 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )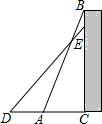 A、0.4 B、0.6 C、0.7 D、0.810. 图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图所示的四边形 . 若 , 且 , 则的长度为( )
A、0.4 B、0.6 C、0.7 D、0.810. 图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图所示的四边形 . 若 , 且 , 则的长度为( ) A、 B、 C、4 D、
A、 B、 C、4 D、二、填空题
-
11. 如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,点C到AB边的距离为.
 12. 在△ABC中,AB=6,AC=5,BC边上的高AD=4,则△ABC的周长为.13. 已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于 cm2 .
12. 在△ABC中,AB=6,AC=5,BC边上的高AD=4,则△ABC的周长为.13. 已知Rt△ABC中,∠C=90°,a+b=14cm,c=10cm,则Rt△ABC的面积等于 cm2 .
14. 某楼梯如图所示,欲在楼梯上铺设红色地毯,已知这种地毯每平方米售价为30元,楼梯宽为2m,则购买这种地毯至少需要元. 15. 如图,一场暴雨过后,垂直于地面的一棵树在距地面米的点处折断,树尖恰好碰到地面,经测量米,则树高为米.
15. 如图,一场暴雨过后,垂直于地面的一棵树在距地面米的点处折断,树尖恰好碰到地面,经测量米,则树高为米.
三、解答题
-
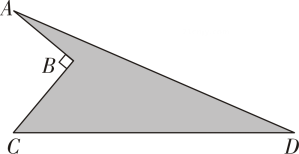
16. 为深入学习贯彻党的二十大精神,贯彻落实习近平总书记关于教育的重要论述和重要指示批示精神,迪庆州某中学计划在如图阴影区域展示学生的学习心得现测得 , , , , 试求阴影部分的面积.
 17. 如图 , 在中, , , 是的高,且 .
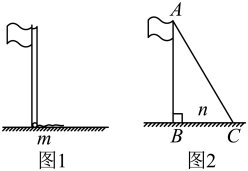
17. 如图 , 在中, , , 是的高,且 . (1)、求的长;(2)、若是边上的一点,作射线 , 分别过点、作于点 , 于点如图 , 若 , 求与的和.18. 如图,数学兴趣小组要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面并多出一段(如图1),聪明的小红发现:先测出垂到地面的绳子长,再将绳子拉直(如图2),测出绳子末端C到旗杆底部B的距离n , 利用所学知识就能求出旗杆的长,若米,米,求旗杆的长.
(1)、求的长;(2)、若是边上的一点,作射线 , 分别过点、作于点 , 于点如图 , 若 , 求与的和.18. 如图,数学兴趣小组要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面并多出一段(如图1),聪明的小红发现:先测出垂到地面的绳子长,再将绳子拉直(如图2),测出绳子末端C到旗杆底部B的距离n , 利用所学知识就能求出旗杆的长,若米,米,求旗杆的长.