人教版初中数学2023-2024学年七年级下学期课时培优练习 5.3平行线的性质
试卷更新日期:2024-01-08 类型:同步测试
一、选择题
-
1. 如图,直线a∥b,Rt△ABC的直角顶点A落在直线a上,点B落在直线b上,若∠1=15°,∠2=25°,则∠ABC的大小为( )
 A、40° B、45° C、50° D、55°2. 下列语句中,是命题的个数为( )
A、40° B、45° C、50° D、55°2. 下列语句中,是命题的个数为( )①若两个角相等,则它们是对顶角;②等腰三角形两底角相等;③画线段;④同角的余角相等;⑤同位角相等.
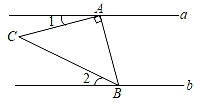
A、2个 B、3个 C、4个 D、5个3. 如图,已知AB∥EF.若∠C=90°,则∠α,∠β,∠γ之间的关系是( ) A、∠β=∠α+∠γ B、∠α+∠β+∠γ=180° C、∠α+∠β-∠γ=90° D、∠β+∠γ-∠α=90°4. 如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )
A、∠β=∠α+∠γ B、∠α+∠β+∠γ=180° C、∠α+∠β-∠γ=90° D、∠β+∠γ-∠α=90°4. 如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )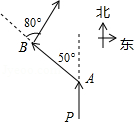 A、北偏东30° B、北偏东80° C、北偏西30° D、北偏西50°5. 如图是一款手推车的平面示意图,其中 , , , 则为( )
A、北偏东30° B、北偏东80° C、北偏西30° D、北偏西50°5. 如图是一款手推车的平面示意图,其中 , , , 则为( )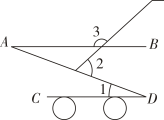 A、66° B、56° C、98° D、104°6. 下列说法正确的个数有( )
A、66° B、56° C、98° D、104°6. 下列说法正确的个数有( )①若 , 则点C是线段的中点;②两点确定一条直线;③射线与射线是同一条射线;④线段就是点A到点B之间的距离;⑤两点之间线段最短.
A、1个 B、2个 C、3个 D、4个7. 如图,直线 , 点在直线上,点、在直线上,且 , 平分 , 若 , 则的度数是( ) A、 B、 C、 D、8. 如图, , 将一副直角三角板作如下摆放, , . 下列结论:①;②;③;④ . 其中正确的个数是( )
A、 B、 C、 D、8. 如图, , 将一副直角三角板作如下摆放, , . 下列结论:①;②;③;④ . 其中正确的个数是( )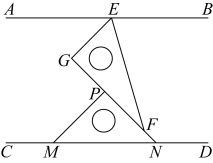 A、1 B、2 C、3 D、49. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )
A、1 B、2 C、3 D、49. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )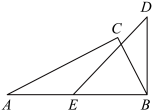 A、或或 B、或或 C、或或 D、或或10. 如图,E在线段的延长线上, , , , 连交于G,的余角比大 , K为线段上一点,连 , 使 , 在内部有射线 , 平分 . 则下列结论:①;②平分;③;④ . 其中正确结论的个数有( )
A、或或 B、或或 C、或或 D、或或10. 如图,E在线段的延长线上, , , , 连交于G,的余角比大 , K为线段上一点,连 , 使 , 在内部有射线 , 平分 . 则下列结论:①;②平分;③;④ . 其中正确结论的个数有( )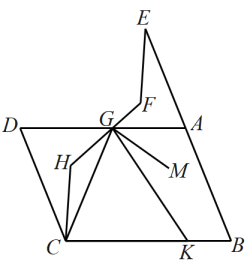 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,已知直线被直线所截, , 点是平面内位于直线右侧的一动点(点不在直线上),设 , 在点运动过程中,的度数可能是 . (结果用含的式子表示)
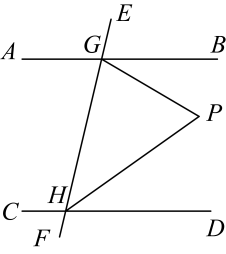 12. 如图,的角平分线、相交于F, , , 且于G.下列结论:①;②平分;③;④ . 其中正确的结论是 .
12. 如图,的角平分线、相交于F, , , 且于G.下列结论:①;②平分;③;④ . 其中正确的结论是 . 13. 为保证安全,某两段铁路两旁安置了两座可旋转探照灯A,B,探照灯的光线可看作射线如图,灯A的光线从射线开始,绕点A顺时针旋转至射线上便立即回转,灯B光线从射线开始,绕点B顺时针旋转至射线便立即回转,两灯不停交叉照射巡视.已知 , 连接 , , 则;若灯B的光线先转动,每秒转动 , 45秒后灯A的光线才开始转动,每秒转动 , 在灯B的光线第一次到达之前,灯A的光线转动秒时,两灯的光线互相平行.
13. 为保证安全,某两段铁路两旁安置了两座可旋转探照灯A,B,探照灯的光线可看作射线如图,灯A的光线从射线开始,绕点A顺时针旋转至射线上便立即回转,灯B光线从射线开始,绕点B顺时针旋转至射线便立即回转,两灯不停交叉照射巡视.已知 , 连接 , , 则;若灯B的光线先转动,每秒转动 , 45秒后灯A的光线才开始转动,每秒转动 , 在灯B的光线第一次到达之前,灯A的光线转动秒时,两灯的光线互相平行.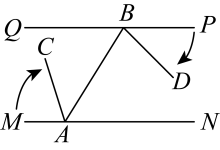 14. 如图,已知 , 、分别在、上,点在、之间,连接、 , , 平分 , 平分 , 在的下方有一点 , 平分 , 平分 , 求的度数为 .
14. 如图,已知 , 、分别在、上,点在、之间,连接、 , , 平分 , 平分 , 在的下方有一点 , 平分 , 平分 , 求的度数为 .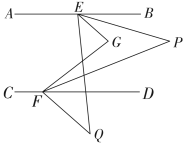 15. 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起,其中 , , , 当 , 且点E在直线的上方时,若这两块三角尺有两条边平行,则
15. 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起,其中 , , , 当 , 且点E在直线的上方时,若这两块三角尺有两条边平行,则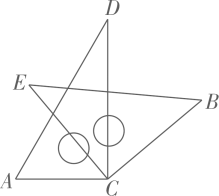
三、解答题
-
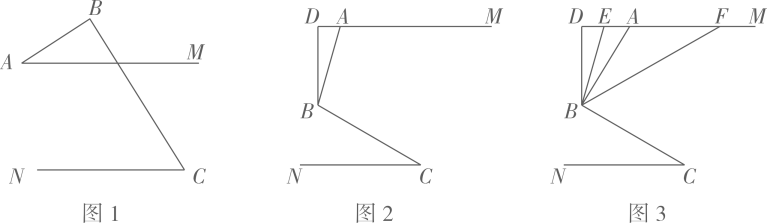
16. 如图,点分别在射线上, .
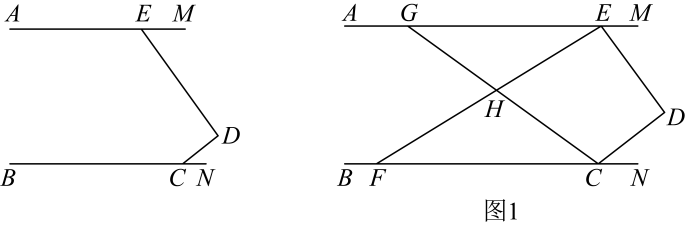 (1)、求证:;(2)、如图1,点G、F在AE、BC上,连接EF、GC,且EF、GC相交于点H,∠AED=n∠AEF,∠BCD=n∠BCG,当∠DEH+∠DCH=2∠EHC时,求n的值.(3)、在(2)条件下,若 , 求证: .17. 如图所示,已知∠1+∠2=180°,∠B=∠3,求证:∠ACB=∠AED.
(1)、求证:;(2)、如图1,点G、F在AE、BC上,连接EF、GC,且EF、GC相交于点H,∠AED=n∠AEF,∠BCD=n∠BCG,当∠DEH+∠DCH=2∠EHC时,求n的值.(3)、在(2)条件下,若 , 求证: .17. 如图所示,已知∠1+∠2=180°,∠B=∠3,求证:∠ACB=∠AED. 18. 如图,直线 , 点、分别在直线、上,点在、之间,连接、 , 直线分别交、于点、 , 平分 , 与交于点已知 , .
18. 如图,直线 , 点、分别在直线、上,点在、之间,连接、 , 直线分别交、于点、 , 平分 , 与交于点已知 , . (1)、若、与互相平行,求的值.(2)、若直线向左平移,且始终平行于求平移过程中点与重合时除外 , 的度数用含的式子表示解答建议:按下列两幅图所示情况分类求解
(1)、若、与互相平行,求的值.(2)、若直线向左平移,且始终平行于求平移过程中点与重合时除外 , 的度数用含的式子表示解答建议:按下列两幅图所示情况分类求解