人教版初中数学2023-2024学年七年级下学期课时基础练习 5.3平行线的性质
试卷更新日期:2024-01-08 类型:同步测试
一、选择题
-
1. 如图,∠AOB的一边OA为一面平面镜,∠AOB=37°36',在OB上有一点E,从点E射出一束光线,经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
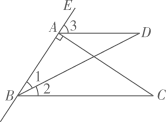
 A、75°36' B、75°12' C、74°36' D、74°12'2. 如图,已知∠1=70°,CD∥BE,则∠B的度数为( )
A、75°36' B、75°12' C、74°36' D、74°12'2. 如图,已知∠1=70°,CD∥BE,则∠B的度数为( )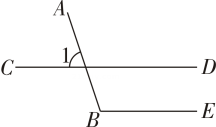 A、70° B、100° C、110° D、120°3. 将一直角三角板与两边平行的纸条如图所示放置,若∠1=55°,则∠2的度数为( )
A、70° B、100° C、110° D、120°3. 将一直角三角板与两边平行的纸条如图所示放置,若∠1=55°,则∠2的度数为( )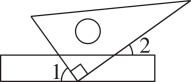 A、135° B、130° C、45° D、35°4. 下列命题中,为真命题的是( )A、两个锐角之和一定为钝角 B、相等的两个角是对顶角 C、同位角相等 D、垂线段最短5. 如图,AB∥CD , OE平分∠BOC , OF⊥OE , OP⊥CD , ∠ABO=n°,则下列结论:①∠COE=90°-n°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF . 其中正确的有( )
A、135° B、130° C、45° D、35°4. 下列命题中,为真命题的是( )A、两个锐角之和一定为钝角 B、相等的两个角是对顶角 C、同位角相等 D、垂线段最短5. 如图,AB∥CD , OE平分∠BOC , OF⊥OE , OP⊥CD , ∠ABO=n°,则下列结论:①∠COE=90°-n°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF . 其中正确的有( ) A、①②③ B、①②④ C、①③④ D、①②③④6. 如图,直线 , 被直线所截,则下列符合题意的结论是( )
A、①②③ B、①②④ C、①③④ D、①②③④6. 如图,直线 , 被直线所截,则下列符合题意的结论是( )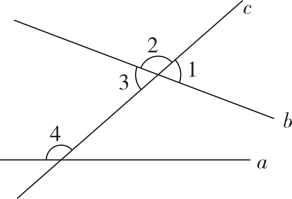 A、 B、 C、 D、7. 如图,直线a b,点B在a上,且AB⊥BC.若∠1=35°,则∠2等于( )
A、 B、 C、 D、7. 如图,直线a b,点B在a上,且AB⊥BC.若∠1=35°,则∠2等于( ) A、35° B、50 C、55° D、65°8. 下列命题中,是真命题的是( )A、在同一平面内,垂直于同一条直线的两条直线平行 B、三角形一个外角大于它的任何一个内角 C、两条直线被第三条直线所截,同旁内角互补 D、过一点有且只有一条直线与已知直线平行9. 将含45°的直角三角板与直尺如图所示放置,有如下结论:(1);(2);(3);(4) , 其中正确的个数是( )
A、35° B、50 C、55° D、65°8. 下列命题中,是真命题的是( )A、在同一平面内,垂直于同一条直线的两条直线平行 B、三角形一个外角大于它的任何一个内角 C、两条直线被第三条直线所截,同旁内角互补 D、过一点有且只有一条直线与已知直线平行9. 将含45°的直角三角板与直尺如图所示放置,有如下结论:(1);(2);(3);(4) , 其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个10. 下列图形中,由AB∥CD , 能得到∠1=∠2的是( )A、
A、1个 B、2个 C、3个 D、4个10. 下列图形中,由AB∥CD , 能得到∠1=∠2的是( )A、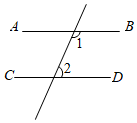 B、
B、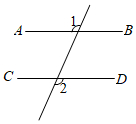 C、
C、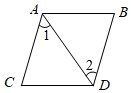 D、
D、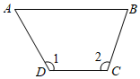
二、填空题
-
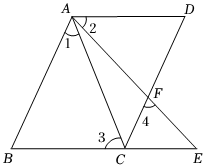
11. 如图,已知AB∥CD,∠2:∠3=1:2,则∠1=°.
 12. 把命题“对顶角相等”改写成“如果…那么…”的形式:13. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若 , 则的度数是 .
12. 把命题“对顶角相等”改写成“如果…那么…”的形式:13. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若 , 则的度数是 .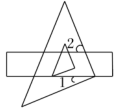 14. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=49°,则∠2﹣∠1= .
14. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=49°,则∠2﹣∠1= .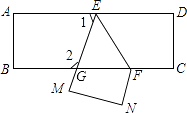 15. 如图,AB∥EF, , , 已知∠FCD=60°,则∠P的度数为 .
15. 如图,AB∥EF, , , 已知∠FCD=60°,则∠P的度数为 .
三、解答题
-
16. 如图,已知AD⊥BC, FG⊥BC,垂足分别为D,G,∠1=∠2,试猜想∠BDE与∠C的大小关系,并说明理由.
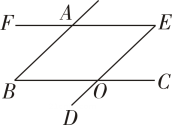
 17. 如图,已知AB∥DE,EF∥BC,DE与BC相交于O,∠B=60°,求∠E的度数.
17. 如图,已知AB∥DE,EF∥BC,DE与BC相交于O,∠B=60°,求∠E的度数.