人教版初中数学2023-2024学年七年级下学期课时培优练习 5.2平行线及其判定
试卷更新日期:2024-01-08 类型:同步测试
一、选择题
-
1. 如图,已知 , 点E为上方一点,、分别为 , 的角平分线,若 , 则的度数为( )
 A、 B、 C、 D、2. 一副三角板按如图所示叠放在一起,其中点、重合,若固定三龟板 , 三角板绕点在平面内旋转,当( )时, .
A、 B、 C、 D、2. 一副三角板按如图所示叠放在一起,其中点、重合,若固定三龟板 , 三角板绕点在平面内旋转,当( )时, .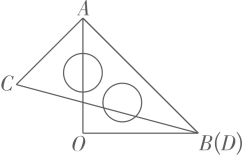 A、 B、或 C、或 D、或3. 如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )
A、 B、或 C、或 D、或3. 如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )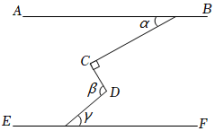 A、α+β-γ=90° B、β=α+γ C、α+β+γ=180° D、β+γ-α=90°4. 如图,已知直线AB、CD被直线AC所截,// , E是平面内任意一点(点E不在直线AB、CD、AC上),设 , . 下列各式:① , ② , ③ , ④ , 的度数可能是( )
A、α+β-γ=90° B、β=α+γ C、α+β+γ=180° D、β+γ-α=90°4. 如图,已知直线AB、CD被直线AC所截,// , E是平面内任意一点(点E不在直线AB、CD、AC上),设 , . 下列各式:① , ② , ③ , ④ , 的度数可能是( )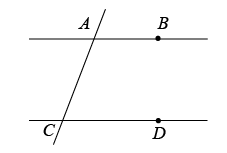 A、①②③ B、①②④ C、②③④ D、①②③④5. 如图a∥b,与相交,与相交,下列说法:
A、①②③ B、①②④ C、②③④ D、①②③④5. 如图a∥b,与相交,与相交,下列说法:①若 , 则;
②若 , 则c∥d;
③;
④ ,
正确的有( )
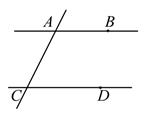
 A、①③④ B、①②③ C、①②④ D、②③6. 如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点 (点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:
A、①③④ B、①②③ C、①②④ D、②③6. 如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点 (点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α-β,③β-α,④360°-α-β,
则∠AEC的度数可能是( )
 A、①②③ B、①②④ C、①③④ D、①②③④7. 如图,AB∥EF,∠ABP= ∠ABC,∠EFP= ∠EFC,已知∠FCD=60°,则∠P的度数为( )
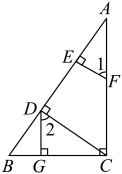
A、①②③ B、①②④ C、①③④ D、①②③④7. 如图,AB∥EF,∠ABP= ∠ABC,∠EFP= ∠EFC,已知∠FCD=60°,则∠P的度数为( ) A、60° B、80° C、90° D、100°8. 如图,在 中, , 是 内角 的平分线, 是 外角 的平分线, 是 外角 的平分线,以下结论不正确的是( )
A、60° B、80° C、90° D、100°8. 如图,在 中, , 是 内角 的平分线, 是 外角 的平分线, 是 外角 的平分线,以下结论不正确的是( ) A、 B、 C、 D、 平分9.
A、 B、 C、 D、 平分9.学习了“平行线”后,张明想出了过已知直线外一点画这条直线的平行线的新方法,他是通过折一张半透明的纸得到的(如图①~④):

从图中可知,张明画平行线的依据有( )
(1)两直线平行,同位角相等; (2)两直线平行,内错角相等;
(3)同位角相等,两直线平行; (4)内错角相等,两直线平行.A、(1)(2) B、(2)(3) C、(1)(4) D、(3)(4)10. 如图,已知AB∥CD, , .则 与 之间满足的数量关系是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
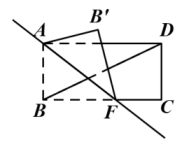
11. 如图,把一张长方形纸片ABCD沿AF折叠,已知∠DBC=20°,当∠BAF=度时,才能使AB'∥BD.
 12. 如图,直线 , 点E、F分别为直线和上的点,点P为两条平行线间的一点,连接和 , 过点P作的平分线交直线于点G,过点F作 , 垂足为H,若 , 则°.
12. 如图,直线 , 点E、F分别为直线和上的点,点P为两条平行线间的一点,连接和 , 过点P作的平分线交直线于点G,过点F作 , 垂足为H,若 , 则°.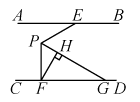 13. 如图,已知长方形纸片 , 点和点分别在边和上,且 , 点和点分别是边和上的动点,现将点 , , , 分别沿 , 折叠至点 , , , , 若 , 则的度数为 .
13. 如图,已知长方形纸片 , 点和点分别在边和上,且 , 点和点分别是边和上的动点,现将点 , , , 分别沿 , 折叠至点 , , , , 若 , 则的度数为 . 14. 如图,已知AB∥CD,E、F、H分别为AB、CD、AC上一点(∠DFK<∠BEK),KG平分∠EKF,∠AEK+∠HKE=180°.则下列结论:①CD∥KH;②∠BEK+∠DFK=2∠EKG;③∠BEK-∠DFK=∠GKH;④∠BAC+∠AGK-∠GKF+∠DFK=180°.其中正确的是 . (填序号)
14. 如图,已知AB∥CD,E、F、H分别为AB、CD、AC上一点(∠DFK<∠BEK),KG平分∠EKF,∠AEK+∠HKE=180°.则下列结论:①CD∥KH;②∠BEK+∠DFK=2∠EKG;③∠BEK-∠DFK=∠GKH;④∠BAC+∠AGK-∠GKF+∠DFK=180°.其中正确的是 . (填序号)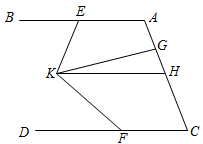 15. 如图ABDE,BF平分∠ABC,反向延长射线BF,与∠EDC的平分线DG相交于点P,若∠BPD=44°,则∠C=.
15. 如图ABDE,BF平分∠ABC,反向延长射线BF,与∠EDC的平分线DG相交于点P,若∠BPD=44°,则∠C=.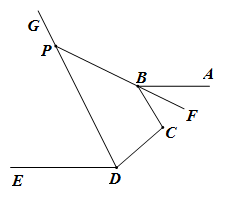
三、解答题
-
16. 如图1,已知 , , , .
 (1)、判断与的位置关系,并说明理由;(2)、当时,求 , 的度数;(3)、如图(2),求 , 的度数(用含m的代数式表示).17. 已知:直线 , 点A和点B是直线a上的点,点C和点D是直线b上的点,连接 , , 设直线和交于点E .
(1)、判断与的位置关系,并说明理由;(2)、当时,求 , 的度数;(3)、如图(2),求 , 的度数(用含m的代数式表示).17. 已知:直线 , 点A和点B是直线a上的点,点C和点D是直线b上的点,连接 , , 设直线和交于点E .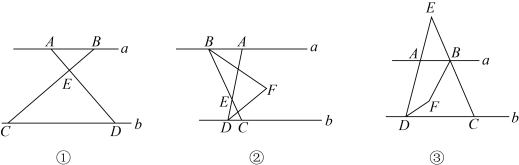 (1)、在如图1所示的情形下,若 , 求的度数;(2)、在如图2所示的情形下,若平分 , 平分 , 且与交于点F , 当 , 时,求的度数;(3)、如图3,当点B在点A的右侧时,若平分 , 平分 , 且 , 交于点F , 设 , , 用含有α , β的代数式表示的补角.
(1)、在如图1所示的情形下,若 , 求的度数;(2)、在如图2所示的情形下,若平分 , 平分 , 且与交于点F , 当 , 时,求的度数;(3)、如图3,当点B在点A的右侧时,若平分 , 平分 , 且 , 交于点F , 设 , , 用含有α , β的代数式表示的补角.