2023-2024学年北师大版数学八年级上册期末仿真模拟卷一

试卷更新日期：2024-01-08 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共36分）

1. 下列各式中，正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $- \sqrt{3^{2}} = - 3$ C、 $\sqrt{{(\pm 3)}^{2}} = \pm 3$ D、 $\sqrt{3^{2}} = \pm 3$

查看试题解析
2. 在平面直角坐标系中，点 $P (2 ， - 3)$ 关于x轴对称的点 $P^{'}$ 的坐标是（）

A、 $(- 2 ， - 3)$ B、 $(- 2 ， 3)$ C、 $(2 ， - 3)$ D、 $(2 ， 3)$

查看试题解析
3. 下列说法正确的是（）

A、检测“神舟十六号”载人飞船零件的质量，应采用抽样调查 B、任意画一个三角形，其外角和是180°是必然事件 C、数据4，9，5，7的中位数是6 D、甲、乙两组数据的方差分别是 $s_{甲}^{2} = 0.4$ ， $s_{乙}^{2} = 2$ ，则乙组数据比甲组数据稳定

查看试题解析
4. 一个直角三角形的两直角边长分别为5和12，则它斜边上的高长为（）

A、13 B、 $\frac{13}{2}$ C、 $\frac{60}{13}$ D、 $\frac{12}{5}$

查看试题解析
5. 估计5 $\sqrt{6}$ ﹣ $\sqrt{24}$ 的值应在（）

A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间

查看试题解析
6. 下列命题是真命题的是（）

A、如果一个数的相反数等于这个数本身，那么这个数一定是0 B、如果一个数的倒数等于这个数本身，那么这个数一定是1 C、如果一个数的平方等于这个数本身，那么这个数一定是0 D、如果一个数的算术平方根等于这个数本身，那么这个数一定是0

查看试题解析
7. 一次函数y=kx﹣1的图象经过点P，且y的值随x值的增大而增大，则点P的坐标可以为（）

A、（﹣5，3） B、（1，﹣3） C、（2，2） D、（5，﹣1）

查看试题解析
8. 已知一次函数 $y = k x + b$ 的图象如图所示，则 $k$ ， $b$ 的取值范围是（）

A、 $k > 0$ ， $b < 0$ B、 $k < 0$ ， $b < 0$ C、 $k < 0$ ， $b > 0$ D、 $k > 0$ ， $b > 0$

查看试题解析
9. 已知方程组 ${\begin{matrix} 2 x + y = 3 \\ x - 2 y = 5 \end{matrix}$ ，则2x+6y的值是（）

A、﹣2 B、2 C、﹣4 D、4

查看试题解析
10. 《孙子算经》中有一道题，原文是：“今有木，不知长短．引绳度之，余绳四足五寸；屈绳量之，不足一尺．木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余 $4.5$ 尺．将绳子对折再量长木，长木还剩余 $1$ 尺，问木长多少尺，现设绳长 $x$ 尺，木长 $y$ 尺，则可列二元一次方程组为（）

A、 ${\begin{array}{l} y - x = 4.5 \\ y - \frac{1}{2} x = 1 \end{array}$ B、 ${\begin{array}{l} x - y = 4.5 \\ y - \frac{1}{2} x = 1 \end{array}$ C、 ${\begin{array}{l} x - y = 4.5 \\ \frac{1}{2} x - y = 1 \end{array}$ D、 ${\begin{array}{l} y - x = 4.5 \\ \frac{1}{2} x - y = 1 \end{array}$

查看试题解析
11. 如果一组数据6，7，x ， 9，5的平均数是2x ，那么这组数据的中位数为（）

A、5 B、6 C、7 D、9

查看试题解析
12. 如图，直线 $m ∥ n$ ， $△ A B C$ 是直角三角形， $∠ B = 90 °$ ，点C在直线n上．若 $∠ 1 = 50 °$ ，则 $∠ 2$ 的度数是（）

A、60° B、50° C、45° D、40°

查看试题解析

二、填空题（每题3分，共18分）

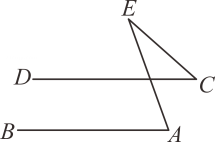
13. 如图，直线 $A B / / C D$ ， $∠ A = 70 °$ ， $∠ C = 40 °$ ，则 $∠ E$ 等于度．

查看试题解析
14. 两组数据m，6，n与1，m，2n，7的平均数都是6，若将这两组数据合并成一组数据，则这组新数据的中位数为．

查看试题解析
15. 如图，在同一平面直角坐标系中，直线l₁：y $= \frac{1}{4}$ x $+ \frac{1}{2}$ 与直线l₂：y＝kx+3相交于点A，则方程组 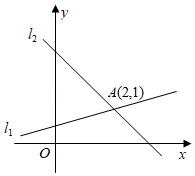${\begin{matrix} y = \frac{1}{4} x + \frac{1}{2} \\ y = k x + 3 \end{matrix}$ 的解为 .

查看试题解析
16. 已知 $m$ 为整数，且一次函数 $y = (m + 4) x + m + 2$ 的图像不经过第二象限，则 $m$ 的值为．

查看试题解析
17. 已知 ${\begin{cases} x = 1 \\ y = 2 \end{cases}$ 是方程组 ${\begin{cases} a x + y = - 1 \\ 2 x - b y = 0 \end{cases}$ 的解，则a+b＝．

查看试题解析
18. 已知一个数的两个平方根分别是2a+4和a+14，则这个数是．

查看试题解析

三、解答题（共8题，共66分）

19. 解方程组：

(1)、 ${\begin{cases} 3 x - y = 7 \\ x + 3 y = - 1 \end{cases}$

(2)、 ${\begin{cases} \frac{x - 1}{6} - \frac{2 - y}{3} = 1 \\ 2 x + y = 13 \end{cases}$

查看试题解析
20. 计算：

(1)、（﹣1）²⁰²³+ $\sqrt{9}$ ﹣π⁰+ $\sqrt{\frac{1}{8}}$ × $\sqrt{32}$ ；

(2)、 $\sqrt{48}$ ÷ $\sqrt{3}$ ﹣ $\sqrt{\frac{1}{2}}$ × $\sqrt{12}$ + $\sqrt{24}$ ．

查看试题解析
21. 下表是小明这一学期数学成绩测试记录，根据表格提供的信息，回答下列问题：
测试
平时成绩
期中测试
期末测试
练习一
练习二
练习三
练习四
成绩
88
92
90
86
90
96

(1)、求小明6次成绩的众数与中位数；

(2)、若把四次练习成绩的平均分作为平时成绩，按照学校规定，本学期的综合成绩的权重如下图所示，请求出小明本学期的综合成绩；

(3)、若全班共有45名同学，综合成绩排名前23的同学可以获得奖励，小明知道了自己的分数后，想知道自己能不能获奖，还需知道全班同学综合成绩的.（填“平均数、中位数、众数、方差”）

查看试题解析
22. 根据小敏、小聪、小东、小强四人的对话内容，请你设计一下，分别安排多少立方米木料做桌面，多少立方米木料做桌腿，才能使得生产出来的桌面和桌腿及库存的桌腿恰好全部配套？

查看试题解析
23. 如图，在平面直角坐标系中，一次函数 $y = k x + b$ 的图象经过点 $A （ - 2 ， 6 ）$ ，且与 $x$ 轴相交于点 $B$ ，与正比例函数 $y = 3 x$ 的图象相交于点 $C$ ，点 $C$ 的横坐标为 $1$ ．

(1)、求 $k$ 、 $b$ 的值；

(2)、请直接写出方程组 $\{\begin{array}{l} k x - y = - b \\ 3 x - y = 0 \end{array}$ 的解；

(3)、若点 $D$ 在 $y$ 轴上，且满足 $S_{△ DOC} = S_{△ BOC}$ ，求点 $D$ 的坐标．

查看试题解析
24. 如图，ED⊥AB，FC⊥AB，垂足分别为D，C，AC=BD，AE=BF．

(1)、求证：DE= CF；

(2)、若CD=DE，∠A=25°，求∠AEC的度数．

查看试题解析
25. 如图，已知OC平分∠AOB，CD⊥OA于点D，E为DC延长线上一点，EF⊥OB于点F，EG平分∠DEF交OB于点G，∠DEF+∠AOB＝180°.

(1)、问题发现：①如图1，当∠AOB＝90°时，∠1+∠2= ▲ °；
②如图2，当∠AOB为锐角时，∠1与∠2有什么数量关系，请说明理由；

(2)、拓展探究：（3）在（2）的条件下，已知直角三角形中两个锐角的和是90°，试探究OC与GE的位置关系，并证明结论．

查看试题解析

测试	平时成绩				期中测试	期末测试
测试	练习一	练习二	练习三	练习四	期中测试	期末测试
成绩	88	92	90	86	90	96