人教版初中数学2023-2024学年七年级下学期课时基础练习 5.2平行线及其判定
试卷更新日期：2024-01-08 类型：同步测试
一、选择题
-
1. 下列结论中，错误的是（ ）A、同位角相等，两直线平行 B、同一平面内过一点有且只有一条直线与已知直线垂直 C、同一平面内的两条直线不平行就相交 D、过一点有且只有一条直线与已知直线平行2. 如图，直线a、b被直线c所截，下列说法正确的是（ ）
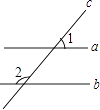A、当∠1=∠2时，一定有a∥b B、当a∥b时，一定有∠1=∠2 C、当a∥b时，一定有∠1+∠2=90° D、当∠1+∠2=180°时，一定有a∥b3. 如图，下列条件中，能判定的是（ ）
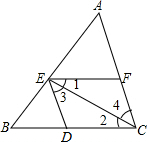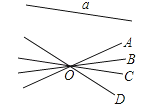
A、 B、 C、 D、4.如图，经过直线a外一点O的4条直线中，与直线a相交的直线至少有（ ）
A、4条 B、3条 C、2条 D、1条5. 如图，直线 ， ， ， ，则 （ ）
A、45° B、55° C、65° D、75°6. 如图， ， 平分 ， 平分 ， 且 ， 下列结论：平分；；；其中结论正确的序号为（ ）
A、 B、 C、 D、7. 一副三角板按如图所示叠放在一起，其中点、重合，若固定三角形 ， 改变三角板的位置其中点位置始终不变 ， 当时， ． （ ）
A、 B、或 C、或 D、或8. 如图1是一个由齿轮、轴承、托架等元件构成的手动变速箱托架，其主要作用是动力传输．如图2是手动变速箱托架工作时某一时刻的示意图，已知AB∥CD，CG∥EF，∠BAG＝150°，∠AGC＝80°，则∠DEF的度数为（ ）
A、110° B、120° C、130° D、140°9. 如图，给出下面的说法：①因为 ， 所以；②因为 ， 所以；③因为 ， 所以；④因为 ， ， 所以 ． 其中正确的是（ ）
A、①②③ B、①②④ C、①③④ D、②③④10. 为增强学生体质，某学校将“抖空竹”引入阳光体育一小时活动.图1是一位同学抖空竹时的一个瞬间，数学老师把它抽象成图2的数学问题：已知 ， ， ， 则的度数为（ ）
A、70° B、50° C、40° D、30°二、填空题
-
11. 如图，若∠B=65°，∠C=15°，∠E=50°，∠DFE=∠E+∠C，则AB与CD的位置关系是.
12. 如图，把一张长方形纸片ABCD沿AF折叠，已知∠DBC=20°，当∠BAF=度时，才能使AB'∥BD．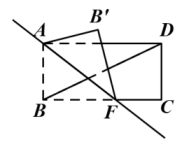
13. 如图， ， 射线 ， 分别与 ， 交于点M ， N ， 若 ， 则的度数是 ．
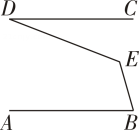
14. 生活中常见一种折叠拦道闸，如图1所示．若想求解某些特殊状态下的角度，需将其抽象为几何图形，如图2所示，垂直于地面于 ， 平行于地面 ， 则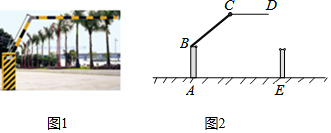
15. 如图，已知直线 ， 点E在和之间，连接 ， 若 ， ， 则 ．
三、解答题
-
16. 如图 ， ， ， 点 ， ， 在同一直线上．
(1)、等于多少度？(2)、若 ， 与平行吗？证明你的结论．17. 如图，已知CF⊥AB ， DE⊥AB ， ∠1＝∠2．试说明：FG∥AC ．
解：∵CF⊥AB ， DE⊥AB（已知），
∴∠DEA＝∠CFA＝90°
∴ ▲ ∥ ▲ ． （同位角相等，两直线平行）
∴∠1＝∠ACF（ ）．
∵∠1＝∠2（已知），
.∴∠ ▲ ＝∠ ▲ （等量代换）．
∴FG∥AC（ ）．
