安徽省阜阳市太和县2023-2024学年八年级上学期月考数学试题
试卷更新日期:2024-01-08 类型:月考试卷
一、选择题(本大题共10小题,每小题4分,满分40分.在每个小题给出的四个选项中,只有一项符合题目要求)
-
1. 下列不是轴对称图形的是( )A、
 B、
B、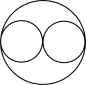 C、
C、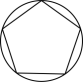 D、
D、 2. 中,如果 , 那么的形状是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定3. 下列计算正确的是( )A、 B、 C、 D、4. 下列判断错误的是( )A、有两角和一边对应相等的两个三角形全等 B、三条边对应相等的两个三角形全等 C、全等三角形对应边上的高相等 D、三个角对应相等的两个三角形全等5. 下列从左到右的变形为因式分解的是( )A、 B、 C、 D、6. 如图,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带上( )
2. 中,如果 , 那么的形状是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定3. 下列计算正确的是( )A、 B、 C、 D、4. 下列判断错误的是( )A、有两角和一边对应相等的两个三角形全等 B、三条边对应相等的两个三角形全等 C、全等三角形对应边上的高相等 D、三个角对应相等的两个三角形全等5. 下列从左到右的变形为因式分解的是( )A、 B、 C、 D、6. 如图,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带上( )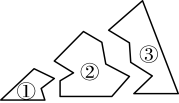 A、① B、② C、③ D、①和③7. 若是个完全平方式,则的值是( )A、6 B、 C、 D、08. 如图,直线 , 等边的顶点C在直线b上,若 , 则的度数为( )
A、① B、② C、③ D、①和③7. 若是个完全平方式,则的值是( )A、6 B、 C、 D、08. 如图,直线 , 等边的顶点C在直线b上,若 , 则的度数为( )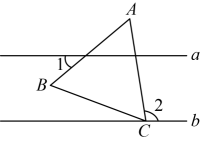 A、 B、 C、 D、9. 如图,若 , 则的度数为( )
A、 B、 C、 D、9. 如图,若 , 则的度数为( ) A、 B、 C、 D、10. 如图,在中, , , 分别以点A和点B为圆心,大于的长为半径画弧,两弧相交于点M , N , 作直线 , 交于点D , 交于点E , 连接 , 若 , 则的长为( )
A、 B、 C、 D、10. 如图,在中, , , 分别以点A和点B为圆心,大于的长为半径画弧,两弧相交于点M , N , 作直线 , 交于点D , 交于点E , 连接 , 若 , 则的长为( )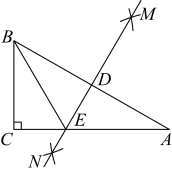 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 如图,在五边形ABCDE中,∠1+∠2+∠3+∠4+∠5=°.
 12. 如图, , 现添加“”,则判定的直接依据是 .
12. 如图, , 现添加“”,则判定的直接依据是 . 13. 长方形的面积是 . 若一边长是 , 则另一边长是 .14. 如图,有两个边长分别为a , b()正方形纸板A , B , 纸板A与B的面积之和为34.现将纸板B按甲方式放在纸板A的内部,阴影部分的面积为4.
13. 长方形的面积是 . 若一边长是 , 则另一边长是 .14. 如图,有两个边长分别为a , b()正方形纸板A , B , 纸板A与B的面积之和为34.现将纸板B按甲方式放在纸板A的内部,阴影部分的面积为4.
① .
② 若将纸板A , B按乙方式并列放置后,构造新的正方形,则阴影部分的面积为 .
三、(本大题共2小题,每小题8分,满分16分)
-
15. 先化简.再求值: , 其中 .16. 若分别为三边的长,且满足 , 试判断的形状,并说明理由.
四、(本大题共2小题,每小题8分,满分16分)
-
17. 如图,在平面直角坐标系中,的三个顶点坐标为 .
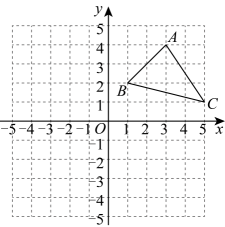 (1)、作出关于y轴的对称图形 .(2)、写出点的坐标: .(3)、在y轴上找一点P , 使的值最小.18. 观察以下等式:
(1)、作出关于y轴的对称图形 .(2)、写出点的坐标: .(3)、在y轴上找一点P , 使的值最小.18. 观察以下等式:第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
……
按照以上规律,解决下列问题:
(1)、写出第5个等式: .(2)、写出你猜想的第个等式(用含的式子表示),并证明.五、(本大题共2小题,每小题10分,满分20分)
-
19. 已知 , 用含a , b的式子表示下列代数式:(1)、 .(2)、 .20. 如图,和均是等边三角形,E , F分别是上的两个动点,且满足 .
 (1)、求证: .(2)、判断的形状,并证明.
(1)、求证: .(2)、判断的形状,并证明.六、(本题满分12分)
-
21. 如图,图1为边长为a的大正方形中有一个边长为b的小正方形,图2是由图1中的阴影部分拼成的一个长方形.
 (1)、设图1中阴影部分的面积为 , 图2中阴影部分的面积为 , 则 , (请用含a , b的代数式表示,只需表示,不必化简).(2)、以上结果可以验证哪个乘法公式?这个乘法公式是(3)、运用(2)中得到的公式,计算: .
(1)、设图1中阴影部分的面积为 , 图2中阴影部分的面积为 , 则 , (请用含a , b的代数式表示,只需表示,不必化简).(2)、以上结果可以验证哪个乘法公式?这个乘法公式是(3)、运用(2)中得到的公式,计算: .七、(本题满分12分)
-
22. 八(2)班数学兴趣小组在一次活动中进行了探究实验活动,请你和他们一起活动吧.

[发现问题]他们在探究实验活动中遇到了下面的问题:如图1,是的中线,若 , 求的取值范围.
[探究方法]他们通过探究发现,延长至点E , 使 , 连接 . 可以证出 , 利用全等三角形的性质可将已知的边长与转化到中,进而求出的取值范围.
方法小结:从上面的思路可以看出,解决问题的关键是将中线延长一倍,构造出全等三角形,我们把这种方法叫做“倍长中线法”.
[问题解决]
(1)、请你利用上面解答问题的思路方法,写出求的取值范围的过程.(2)、如图2,是的中线,且 , 求证: .八、(本题满分14分)
-
23. 阅读材料:我们把多项式及叫做完全平方式.如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式的最大值和最小值等.例如分解因式:
.
又例如:求代数式的最小值,因为 ,
又因为 , 所以当时,有最小值,最小值是 .
根据阅读材料,利用“配方法”,解决下列问题:
(1)、分解因式: .(2)、当x为何值时,多项式有最小值?并求出这个最小值.(3)、试说明:无论y取任何实数时,多项式的值总为正数.
-
-