安徽省蚌埠市蚌山区G5教研联盟2023-2024学年八年级上学期月考数学试题
试卷更新日期:2024-01-08 类型:月考试卷
一、选择题(本大题共10小题,每小题4分,满分40分,在每小题给出的四个选项中,只有一个是符合题目要求的)
-
1. 下列关于体育运动的图标是轴对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 2. 函数中,自变量的取值范围是( )A、 B、 C、 D、3. 已知点 , 若 , , 则点P所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列选项中,可以用来证明命题“若 , 则 . ”是假命题的反例的是( )A、 B、 C、 D、5. 如图,在中, , , 是边上两点, , 平分 , 下列说法中不正确的是( )
2. 函数中,自变量的取值范围是( )A、 B、 C、 D、3. 已知点 , 若 , , 则点P所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列选项中,可以用来证明命题“若 , 则 . ”是假命题的反例的是( )A、 B、 C、 D、5. 如图,在中, , , 是边上两点, , 平分 , 下列说法中不正确的是( )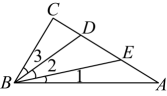 A、是的中线 B、是的角平分线 C、 D、是的高6. 根据下列条件,不能画出唯一的是( )A、 , , B、 , , C、 , , D、 , ,7. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、8. 如图,和关于直线l对称,连接 , 其中与直线l交于点O , 点D为直线l上一点,且不与点O重合,连接 . 下列说法错误的是( )
A、是的中线 B、是的角平分线 C、 D、是的高6. 根据下列条件,不能画出唯一的是( )A、 , , B、 , , C、 , , D、 , ,7. 已知一次函数 的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )A、 B、 C、 D、8. 如图,和关于直线l对称,连接 , 其中与直线l交于点O , 点D为直线l上一点,且不与点O重合,连接 . 下列说法错误的是( ) A、 B、线段被直线l垂直平分 C、为等腰三角形 D、线段所在直线的交点不一定在直线l上9. 如图,在中, , , 点E , F分别是上的点,沿着将折叠得到 . 若 , 则的度数为( )
A、 B、线段被直线l垂直平分 C、为等腰三角形 D、线段所在直线的交点不一定在直线l上9. 如图,在中, , , 点E , F分别是上的点,沿着将折叠得到 . 若 , 则的度数为( )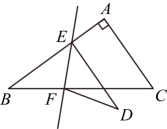 A、 B、 C、 D、10. 如图,正方形的边长为 , 动点从点出发沿折线做匀速运动,设点运动的路程为 , 的面积为 , 下列图象能表示与之间函数关系的是( )
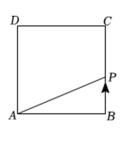
A、 B、 C、 D、10. 如图,正方形的边长为 , 动点从点出发沿折线做匀速运动,设点运动的路程为 , 的面积为 , 下列图象能表示与之间函数关系的是( )
 A、
A、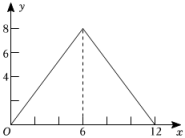 B、
B、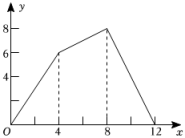 C、
C、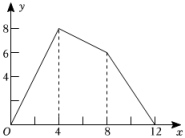 D、
D、
二、填空题(本大题共5小题,每小题4分,满分20分)
-
11. 在平面直角坐标系中,将点向右平移3个单位长度后,再向下平移2个单位长度,得到点 , 则点的坐标为 .12. 如图, , 若 , , 则的长为 .
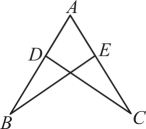 13. 已知一次函数(k是常数且)的图象始终经过点 , 则a的值为 .14. 某品牌鞋子的长度ycm与鞋子的“码”数x之间满足一次函数关系.若22码鞋子的长度为16cm,44码鞋子的长度为27cm,则38码鞋子的长度为cm.15. 如图,在中, , . 为边上的垂直平分线,若点D在直线上,连接 , , 则周长的最小值为 .
13. 已知一次函数(k是常数且)的图象始终经过点 , 则a的值为 .14. 某品牌鞋子的长度ycm与鞋子的“码”数x之间满足一次函数关系.若22码鞋子的长度为16cm,44码鞋子的长度为27cm,则38码鞋子的长度为cm.15. 如图,在中, , . 为边上的垂直平分线,若点D在直线上,连接 , , 则周长的最小值为 .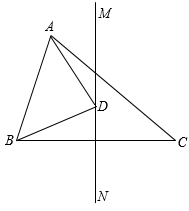
三、解答题(本大题共8小题,满分90分)
-
16. 已知在同一平面内的两条相等线段,通过一次或两次轴对称变化就可以重合.如图方格纸中的每个小方格都是边长为1个单位长度的正方形,点都在格点上,请分别在下面两个图中画出对称轴,使得线段通过轴对称变化与线段重合;若需两次轴对称的,则要画出第一次轴对称后的对称线段.
 17. 如图,点F、C在BE上,BF=CE,AB=DE,∠B=∠E.
17. 如图,点F、C在BE上,BF=CE,AB=DE,∠B=∠E.求证:AC=DF.
 18. 已知一次函数的图象经过点和点 .(1)、求直线的解析式;(2)、求直线与坐标轴所围成的三角形的面积.19. 如图,在四边形中, , , 我们把这种两组邻边分别相等的四边形叫做“筝形”.
18. 已知一次函数的图象经过点和点 .(1)、求直线的解析式;(2)、求直线与坐标轴所围成的三角形的面积.19. 如图,在四边形中, , , 我们把这种两组邻边分别相等的四边形叫做“筝形”. (1)、求证:;(2)、直线是线段的垂直平分线吗?请说明理由.20. 某中学组织开展“回顾党史,重温初心”的红色研学旅行,估计人数在15~25之间.甲、乙两家旅行社原价均为200元/人,甲旅行社优惠方案:所有人八折优惠;乙旅行社优惠方案:10人以内(含10人)按原价收费,超过的人数每人费用降低40%.(1)、分别写出两家旅行社旅行费用y(元)与人数x之间的函数关系式;(2)、若有18人参加旅游,选择哪家旅行社比较划算?21. 如图,在中, , 是的角平分线,于 , 点在边上.连接 .
(1)、求证:;(2)、直线是线段的垂直平分线吗?请说明理由.20. 某中学组织开展“回顾党史,重温初心”的红色研学旅行,估计人数在15~25之间.甲、乙两家旅行社原价均为200元/人,甲旅行社优惠方案:所有人八折优惠;乙旅行社优惠方案:10人以内(含10人)按原价收费,超过的人数每人费用降低40%.(1)、分别写出两家旅行社旅行费用y(元)与人数x之间的函数关系式;(2)、若有18人参加旅游,选择哪家旅行社比较划算?21. 如图,在中, , 是的角平分线,于 , 点在边上.连接 . (1)、求证:;(2)、若 , , , 则求的长(用含 , 的代数式表示).
(1)、求证:;(2)、若 , , , 则求的长(用含 , 的代数式表示).