人教版初中数学2023-2024学年七年级下学期课时培优练习 5.1相交线

试卷更新日期：2024-01-08 类型：同步测试

进入出卷网下载

一、选择题

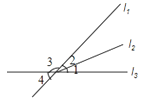
1. 如图，下列6种说法：①∠1与∠4是内错角；②∠1与∠2是同位角；③∠2与∠4是内错角；④∠4与∠5是同旁内角；⑤∠2与∠4是同位角；⑥∠2与∠5是内错角．其中正确的有 ( )

A、1个 B、2个 C、3个 D、4个

查看试题解析
2.
在下列语句中，正确的是（）．

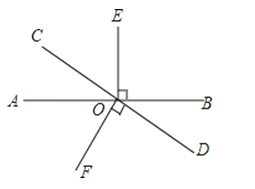
A、在平面上，一条直线只有一条垂线; B、过直线上一点的直线只有一条; C、过直线上一点且垂直于这条直线的直线有且只有一条; D、垂线段的长度就是点到直线的距离

查看试题解析
3. 如图所示，OA⊥OC，OB⊥OD，下面结论中，其中说法正确的是（　　）
①∠AOB＝∠COD；②∠AOB＋∠COD＝90°；③∠BOC＋∠AOD＝180°；④∠AOC－∠COD＝∠BOC.

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
4. 小明在做一道数学题．直线AB，CD相交于点O，∠BOC＝25°，过点O作 $O E ⊥ C D$ ，求∠AOE的度数．小明得到 $∠ A O E = 65 °$ ，但老师说他少了一个答案．那么∠AOE的另一个值是（）

A、105° B、115° C、125° D、135°

查看试题解析
5. 如图，点A在直线l₁上，点B，C在直线l₂上，AB⊥l₂于点B，AC⊥l₁于点A，AB＝4，AC＝5，则下列说法正确的是（　　）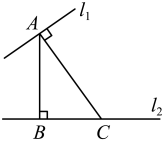

A、点B到直线l₁的距离等于4 B、点A到直线l₂的距离等于5 C、点B到直线l₁的距离等于5 D、点C到直线l₁的距离等于5

查看试题解析
6. 用“垂线段最短”来解释的现象是（　　）

A、测量跳远成绩 B、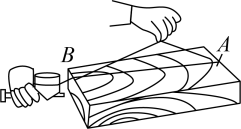木板上弹墨线 C、两钉子固定木条 D、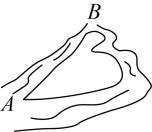弯曲河道改直

查看试题解析
7. 如图所示， $∠ B A C = 90 ° ， A D ⊥ B C$ 于D，则下列结论中，正确的个数为（　）
① $A B ⊥ A C$ ；② $A D$ 与 $A C$ 互相垂直；③点C到 $A B$ 的垂线段是线段 $A B$ ；④点A到 $B C$ 的距离是线段 $A D$ 的长度；⑤线段 $A C$ 的长度是点C到 $A B$ 的距离；⑥线段 $C D$ 的长度是点D到 $A C$ 的距离．

A、3个 B、4个 C、7个 D、0个

查看试题解析
8. 如图：已知AB⊥BC，垂足为B，AB＝3.5，点P是射线BC上的动点，则线段AP的长不可能是（）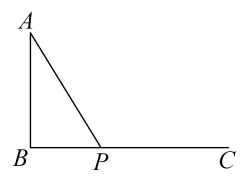

A、3 B、3.5 C、4 D、5

查看试题解析
9. 下列说法中正确的是（）

A、有且只有一条直线与已知直线垂直； B、从直线外一点到这条直线的垂线段，叫做这点到这条直线距离； C、互相垂直的两条线段一定相交； D、直线 $l$ 外一点 $A$ 与直线 $l$ 上各点连接而成的所有线段中，最短线段的长度是 $3 c m$ ，则点 $A$ 到直线 $l$ 的距离是 $3 c m$ .

查看试题解析
10. 中国滑雪天才少女谷爱凌在2022年北京冬奥会的赛场上斩获“自由式滑雪大跳台”首金，这是她获得的首个冬奥会奖牌，也是中国运动员第一次参加冬奥会大跳台的比赛．项目图标如下图；则在下列判断中①∠1与∠2是对顶角；②∠3与∠4是同旁内角；③∠5与∠6是同旁内角；④∠1与∠4是内错角，其中正确的有（）个．

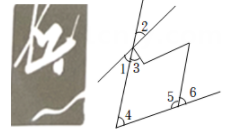A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 如图，直线 $A B 、 C D$ 交于点O ， $O E ⊥ C D$ ， $∠ E O F = 142 ° ， ∠ D O F = 2 ∠ B O D$ ，则 $∠ A O C$ 的度数为．

查看试题解析
12. 如图，点O在直线 $A B$ 上，过点O作射线 $O C$ ， $O D$ ， $O E$ ．从下面的四个条件中任选两个，可以推出 $∠ 2 = ∠ 4$ 的是（写出一组满足题意的序号）．
① $O C ⊥ A B$ ；② $∠ 1$ 和 $∠ 4$ 互余；③ $O D ⊥ O E$ ；④ $∠ 1 = ∠ 4$ ．

查看试题解析
13. 如图，直线AB与CD相交于点O，OE⊥CD，OF平分∠AOE，∠COF＝34°，则∠BOD的度数为．

查看试题解析
14. 已知直线AB与直线CD相交于点O，∠AOC：∠BOC＝2：1，射线OE⊥CD，则∠AOE的度数为．

查看试题解析
15. 如图，AB与BC被AD所截得的内错角是；DE与AC被直线AD所截得的内错角是；图中∠4的内错角是．

查看试题解析

三、解答题

16. 已知：点 $O$ 为直线 $A B$ 上一点，过点 $O$ 作射线 $O C$ ， $∠ B O C = 11 0^{∘}$ ．

(1)、如图1，求 $∠ A O C$ 的度数；

(2)、如图2，过点 $O$ 作射线 $O D$ ，使 $∠ C O D = 9 0^{∘}$ ，作 $∠ A O C$ 的平分线 $O M$ ，求 $∠ M O D$ 的度数；

(3)、如图3，在（2）的条件下，作射线 $O P$ ，若 $∠ B O P$ 与 $∠ A O M$ 互余，请画出图形，并求 $∠ C O P$ 的度数．

查看试题解析
17. 如图，已知直线 $A B$ 和 $C D$ 交于点O， $O E ⊥ A B$ ， $O F$ 平分 $⊥ B O D$ ， $∠ C O E = 20 °$ ，求 $∠ A O C$ ， $∠ B O F$ 的度数．

查看试题解析
18. 如图，直线AB、CD、EF相交于点O，OG平分∠COF，∠1=30°，∠2=45°．求∠3的度数．

查看试题解析
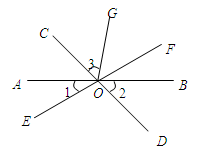19. 如图，AD⊥BC于点D，EF⊥BC于点F，∠BDG＝∠C．试说明∠1＝∠2．

查看试题解析
20.
如图所示，L₁ ， L₂ ， L₃交于点O，∠1=∠2，∠3：∠1=8：1，求∠4的度数．

查看试题解析
21.
如图，直线AB，CD相交于点O，OE⊥AB，OF⊥CD．
（1）若OC恰好是∠AOE的平分线，则OA是∠COF的平分线吗？请说明理由；
（2）若∠EOF=5∠BOD，求∠COE的度数．

查看试题解析
22.
如图：
（1）找出直线DC，AC被直线BE所截形成的同旁内角．
（2）指出∠DEF与∠CFE是由哪两条直线被哪一条直线所截形成的什么角．
（3）试找出图中与∠DAC是同位角的所有角．

查看试题解析