2023-2024学年浙教版数学八年级（上）期末仿真模拟卷（三）

试卷更新日期：2024-01-07 类型：期末考试

进入出卷网下载

一、选择题（每题4分，共40分）

1. 下列图标是节水、节能、低碳和绿色食品的标志，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，在△ABC中，∠BCA＝40°，∠ABC＝60°．若BF是△ABC的高，与角平分线AE相交于点O，则∠EOF的度数为（　　）

A、130° B、70° C、110 D、100°

查看试题解析
3. 如图， $△ A B C$ 中， $A B = A C$ ， AD平分 $∠ B A C$ ， $D E ⊥ A B$ ， $D F ⊥ A C$ ，垂足分别是E、F，则下列四个结论中：①AD上任意一点到B、C的距离相等；②AD任意一点到AB、AC的距离相等；③ $A D ⊥ B C$ 且 $B D = C D$ ；④ $∠ B D E = ∠ C D F$ ．其中正确的是（）

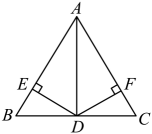A、①④ B、②④ C、②③④ D、①②③④

查看试题解析
4. 下列命题真命题的个数有（）
①过一点有且只有一条直线与已知直线平行；
②直线外一点与直线上各点连接的所有线段中，垂线段最短；
③若 $a > b$ ，则 $c - a > c - b$ ；
④无理数都是无限小数；
⑤平方根等于本身的数是 $0$ 和 $1$ ．

A、 $4$ 个 B、 $3$ 个 C、 $2$ 个 D、 $1$ 个

查看试题解析
5. 已知关于x的不等式 $2 x + a ⩽ 1$ 只有两个正整数解，则 $a$ 的取值范围为（）

A、 $- 5 < a < - 3$ B、 $- 5 ⩽ a < - 3$ C、 $- 5 < a ⩽ - 3$ D、 $- 5 ⩽ a ⩽ - 3$

查看试题解析
6. 如图，已知 $∠ A B C$ ，以点B为圆心，适当长为半径作弧，分别交 $A B ， B C$ 于D，P；作一条射线 $F E$ ，以点F圆心， $B D$ 长为半径作弧l，交 $E F$ 于点H；以H为圆心， $P D$ 长为半径作弧，交弧 $l$ 于点Q；作射线 $F Q$ .这样可得 $∠ G F E = ∠ A B C$ ，其依据是（）

A、 $S S S$ B、 $S A S$ C、 $A S A$ D、 $A A S$

查看试题解析
7. 已知点A的坐标为（a+1，3﹣a），下列说法正确的是（）

A、若点A在y轴上，则a＝3 B、若点A在一三象限角平分线上，则a＝1 C、若点A到x轴的距离是3，则a＝±6 D、若点A在第四象限，则a的值可以为﹣2

查看试题解析
8. 在平面内，下列说法不能确定物体位置的是（）

A、某影厅3排5座 B、北偏西30° C、某市解放路30号 D、东经110°，北纬30°

查看试题解析
9. 函数 $y = \sqrt{x + 5}$ 的自变量x的取值范围是（）

A、 $x > 5$ B、 $x < 5$ C、 $x \neq - 5$ D、 $x \geq - 5$

查看试题解析
10. 为培养同学们的创新精神，某校举办校园科技节活动，八年级同学进行了机器人行走性能试验．在试验场地有A，B，C三点顺次在同一笔直的赛道上，甲、乙两机器人分别从A，B两点同时同向出发，历时8分钟同时到达C点，乙机器人始终以60米/分的速度行走，如图是甲、乙两机器人之间的距离y（米）与它们的行走时间x（分钟）之间的函数图象，若前3.5分钟甲机器人的速度不变，则出发（）分钟后两机器人最后一次相距6米．

A、6 B、6.4 C、6.8 D、7.2

查看试题解析

二、填空题（每题4分，共24分）

11. 已知：如图，△ABC和△BAD中，∠C=∠D=90°，再添加一个条件就可以判断△ABC≌△BAD.

查看试题解析
12. 如图，在△AOB中，∠AOB＝90°，AO＝2，AB＝2 $\sqrt{10}$ ，将△AOB绕顶点O逆时针旋转到△A′OB′处，此时线段A′B′与BO的交点E为BO的中点，线段B′E的长为．

查看试题解析
13. 已知关于x的不等式组 ${\begin{array}{l} x - a ⩾ 0 \\ 3 - 2 x > - 1 \end{array}$ 的整数解有3个，则a的取值范围是．

查看试题解析
14. 将点P(-1，2)向左平移2个单位，再向上平移1个单位所得的对应点的坐标为。

查看试题解析
15. 已知一次函数 $y = (k + 4) x + k^{2} - 16$ 的图象经过原点，则k的值为．

查看试题解析
16. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ 于点 $D$ ， $D E ⊥ A B$ 于点 $E ．$ 若 $∠ B = 30 °$ ， $A E = 1$ .

(1)、 $B E$ 的长为；

(2)、在 $△ A B C$ 的腰上取一点 $M$ ，当 $△ D E M$ 是等腰三角形时， $B M$ 长为.

查看试题解析

三、综合题

17.

(1)、解不等式 $\frac{1 - x}{3} ⩽ \frac{1 - 2 x}{7}$ ，并把它的解集表示在数轴上．

(2)、解不等式组 ${\begin{array}{l} 5 x - 1 > 3 (x + 1) \\ \frac{1}{2} x - 1 ⩽ 7 - \frac{3}{2} x \end{array}$ ．

查看试题解析
18. 如图

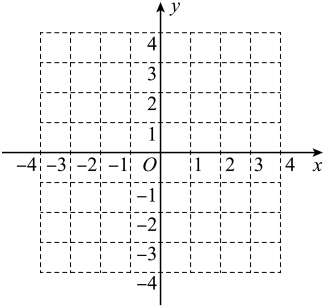(1)、在平面直角坐标系中，画 $△ A B C$ ，使其三个顶点为 $A (- 1 ， 0)$ ， $B (1 ， - 1)$ ， $C (3 ， 3)$ ；

(2)、 $△ A B C$ 是直角三角形吗？请证明你的判断.

查看试题解析
19. 如图，直线y=2x+3与x轴相交于点A，与y轴相交于点B.

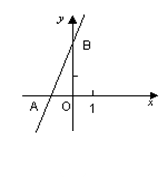(1)、求△AOB的面积；

(2)、过B点作直线BP与x轴相交于P，△ABP的面积是 $\frac{9}{2}$ ，求点P的坐标.

查看试题解析
20. 如图，一根直立的旗杆高8m，因刮大风旗杆从点C处折断，顶部B着地且离旗杆底部A的距离为4m．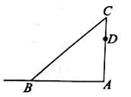

(1)、求旗杆距地面多高处折断（ $A C$ ）；

(2)、工人在修复的过程中，发现在折断点C的下方1m的点D处，有一条明显裂痕，将旗杆修复后，若下次大风将旗杆从点D处吹断，则距离旗杆底部周围多大范围内有被砸伤的风险？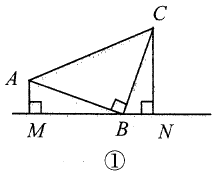

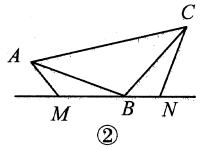查看试题解析
21. 如图，在 $△ A B C$ 中， $A B = B C$ ．

(1)、如图①所示，直线 $N M$ 过点 $B$ ， $A M ⊥ M N$ 于点 $M$ ， $C N ⊥ M N$ 于点 $N$ ，且 $∠ A B C = 90 °$ ．求证： $M N = A M + C N$ ．

(2)、如图②所示，直线 $M N$ 过点 $B$ ， $A M$ 交 $M N$ 于点 $M$ ， $C N$ 交 $M N$ 于点 $N$ ，且 $∠ A M B = ∠ A B C = ∠ B N C$ ，则 $M N = A M + C N$ 是否成立？请说明理由．

查看试题解析
22. 如图，在△ABC中，AB＝AC，∠A＝36°，AC的垂直平分线DE分别交AB，AC于点D，E.

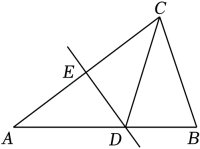(1)、求证：△BCD是等腰三角形；

(2)、若△BCD的周长是13，BC＝5，求AC的长.

查看试题解析
23. 如图，在下面的直角坐标系中，已知A（0，a），B（b，0），C（b，4）三点，其中a，b满足关系式 $a = \frac{\sqrt{b^{2} - 9} + \sqrt{9 - b^{2}}}{b + 3} + 2$ .

(1)、求a，b的值；

(2)、如果在第二象限内有一点P(m， $\frac{1}{3}$ )，请用含m的式子表示四边形ABOP的面积；

(3)、在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等?若存在，求出点P的坐标；若不存在，请说明理由.

查看试题解析
24. 如图，在平面直角坐标系中，直线 $l_{1}$ ： $y = k x + 1$ 交y轴于点A，交x轴于点B（4，0），过点E（2，0）的直线 $l_{2}$ 平行于y轴，交直线 $l_{1}$ 于点D，点P是直线 $l_{2}$ 上一动点（异于点D），连接 $P A$ 、 $P B$ .

(1)、直线 $l_{1}$ 的表达式为，点D的坐标为；

(2)、设P（2，m），当点P在点D的下方时，求 $△ A B P$ 的面积S的表达式（用含m的代数式表示）；

(3)、当 $△ A B P$ 的面积为3时，则以点B为直角顶点作等腰直角 $△ B P C$ ，请直接写出点C的坐标.

查看试题解析