山东省临沂市沂南县2023-2024学年九年级上学期期中数学试卷

试卷更新日期：2024-01-05 类型：期中考试

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分）在每小题所给的四个选项中，只有一项是符合题目要求的.

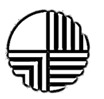
1. 下列方程中，是一元二次方程的是（　　）

A、x³+2x＝0 B、x（x﹣3）＝0 C、 $\frac{1}{x^{2}} - x = 1$ D、y﹣x²＝4

查看试题解析
2. 中秋节是中国的传统节日，有“团圆”、“丰收”的寓意．月饼是首选传统食品，不仅美味，而且设计多样．下列月饼图案中，为中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如若关于x的方程x²+ax+6＝0有一个根为﹣3，则a的值是（　　）

A、9 B、5 C、3 D、﹣3

查看试题解析
4. 已知⊙O的半径为10，OP＝8，则点P与⊙O的位置关系是（　　）

A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、不确定

查看试题解析
5. 根据下列表格中二次函数y＝ax²+bx+c的自变量x与y的对应值，判断关于x的一元二次方程ax²+bx+c＝0的一个解的大致范围是（　　）
x
﹣1
0
1
2
3
4
y
﹣7
﹣5
﹣1
5
13
23

A、1＜x＜2 B、﹣1＜x＜1 C、﹣7＜x＜﹣1 D、﹣1＜x＜5

查看试题解析
6. 将抛物线y＝x²向左平移3个单位，再向上平移2个单位，得到抛物线的表达式为（　　）

A、y＝（x+3）²+2 B、y＝（x+3）²﹣2 C、y＝（x﹣3）²+2 D、y＝（x﹣3）²﹣2

查看试题解析
7. 如图，将△ABC绕点C逆时针旋转一定的角度得到△A′B′C ，此时点A在边B′C上，若BC＝5，A′C＝3，则AB′的长为（　　）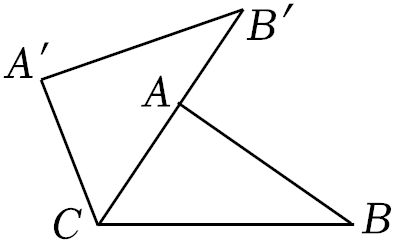

A、2 B、3 C、4 D、5

查看试题解析
8. 如果关于x的一元二次方程x²﹣6x+9k＝0有两个不相等的实数根，那么k的取值范围是（　　）

A、k＜1 B、k≠0 C、k≤1 D、k＞1

查看试题解析
9. 若二次函数y＝（x﹣3）²+2的图象过A（﹣1，y₁），B（2，y₂），C（3.5，y₃），则y₁ ， y₂ ， y₃的大小关系是（　　）

A、y₂＞y₁＞y₃ B、y₃＞y₂＞y₁ C、y₃＞y₁＞y₂ D、y₁＞y₂＞y₃

查看试题解析
10. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值：
x
…
﹣2
0
1
3
…
y
…
6
﹣4
﹣6
﹣4
…
下列选项中，正确的是（　　）

A、这个函数的开口向下 B、这个函数的图象与x轴无交点 C、当x＞2时，y的值随x的增大而减小 D、这个函数的最小值小于﹣6

查看试题解析
11. （多选）如图，已知锐角∠AOB ，按如下步骤作图：（1）在射线OA上取一点C ，以点O为圆心，OC长为半径作 $\hat{P Q}$ ，交射线OB于点D ，连接CD；（2）分别以点C ， D为圆心，CD长为半径作弧，交 $\hat{P Q}$ 于点M ， N；③连接OM ， MN ， ND ．根据以上作图过程及所作图形，下列结论中正确的是（　　）

A、∠COM＝∠COD B、若OM＝MN ，则∠AOB＝20° C、MN∥CD D、∠COD＝3∠MND

查看试题解析
12. 如图是二次函数y＝ax²+bx+c（a≠0）的部分图象，顶点坐标为（﹣1，﹣2）．下列结论：①b＞0；②方程ax²+bx+c+2＝0有两个相等的实数根；③a+b+c＞0；④a﹣c＝2．其中所有正确结论的序号是（　　）

A、①②③④ B、②③④ C、①③④ D、①②③

查看试题解析

二、填空题（每小题3分，共12分）

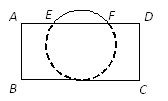
13. 抛物线y＝x²+2x﹣4与y轴的交点坐标是．

查看试题解析
14. 为了让学生养成热爱图书的习惯，某学校抽出一部分资金用于购买书籍．已知2020年该学校用于购买图书的费用为5000元，2022年用于购买图书的费用是7200元，则2020﹣2022年买书资金的平均增长率是．

查看试题解析
15. 把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=4cm ，则球的半径为cm.

查看试题解析
16. 一副三角板按如图所示放置，将含30°角的三角板固定，含45°角的三角板绕A点旋转，保持∠1为锐角，旋转过程中有下列结论：①∠1＝∠3；②若∠2＝45°，则AC∥DE．③若∠4＝∠B，则AC∥DE；④若∠1＝15°，则BC∥DE．其中正确的有．（填序号）

查看试题解析

三、解答题（本大题共7小题，共72分）

17. 已知：关于x的方程x²+kx﹣2＝0的一个根是2，求另一个根及k的值．

查看试题解析
18. 如图，在平面直角坐标系中，△ABC的顶点C的坐标为（﹣4，1）．

(1)、画出△A₁B₁C₁ ，使得△A₁B₁C₁与△ABC关于原点O对称，并写出C₁的坐标；

(2)、以O为旋转中心，将△ABC逆时针旋转90°得到△A₂B₂C₂ ，画出△A₂B₂C₂并写出C₂的坐标．

查看试题解析
19. 某电商店铺销售一种儿童服装，其进价为每件50元，现在的销售单价为每件80元，每周可卖出200件，双十二期间，商家决定降价让利促销，经过市场调查发现，单价每件降低1元，每周可多卖出20件．

(1)、若想满足每周销售利润为7500元，同时尽可能让利于顾客，则每件童服装应降价多少元？

(2)、该店铺每周可能盈利10000元吗？请说明理由．

查看试题解析
20. 已知：二次函数y＝﹣x²+2x+3．

(1)、选取适当的数据填入下表，并在图中的直角坐标系内描点画出该抛物线的图象；
x
…

…
y
…

…

(2)、当﹣1＜x＜2时，观察图象，直接写出函数值y的取值范围．

查看试题解析
21. 如图，在△ABC中，点E在BC边上，AE＝AB ，将线段AC绕A点旋转到AF的位置，使得∠CAF＝∠BAE ，连接EF ， EF与AC交于点G ．

(1)、求证：BC＝EF；

(2)、若∠ABC＝64°，∠ACB＝25°，求∠AGE的度数．

查看试题解析
22. 如图，在 $△ A B C$ 中， $A B = A C$ ，以 $A B$ 为直径的⊙O交 $B C$ 于点D，过点D作 $E F ⊥ A C$ 于点E，交 $A B$ 的延长线于点F．

(1)、求证： $E F$ 是⊙O的切线；

(2)、当 $A B = 5$ ， $B C = 6$ 时，求 $D E$ 的长．

查看试题解析
23. 如图1，劳动课同学们利用喷水头喷出的水对草坪进行喷灌作业以养护草坪．如图2，点O处有一个喷水头，距离喷水头8m的M处有一棵高度是2.4m的树，距离这棵树10m的N处有一面高1.8m的围墙．建立如图所示平面直角坐标系．已知喷水头喷出的水柱的竖直高度y（m）与水平距离x（m）近似满足函数关系y＝ax²+bx+c（a＜0）．

(1)、某次喷水浇灌时，测得x与y的几组数据如下：
x
0
2
6
10
12
y
0
0.88
2.16
2.80
2.88
①根据上述数据，求满足的函数关系；
②求喷水头喷出的水柱最大高度；

(2)、又一次喷水浇灌时，已知喷水头喷出的水柱的竖直高度y与水平距离x近似满足函数关系y＝﹣0.04x²+bx ，假设喷水头喷出的水柱能够越过这棵树，且不会浇到墙外，求出同时满足这两个要求的常数b的范围．

查看试题解析

x	﹣1	0	1	2	3	4
y	﹣7	﹣5	﹣1	5	13	23

x	…	﹣2	0	1	3	…
y	…	6	﹣4	﹣6	﹣4	…

x	…						…
y	…						…

x	0	2	6	10	12
y	0	0.88	2.16	2.80	2.88