北师大版数学八年级上册期末冲刺满分攻略2 勾股定理的逆定理
试卷更新日期:2024-01-05 类型:复习试卷
一、选择题
-
1. 下列条件中,不能判断△ABC是直角三角形的是( )A、a:b:c=3:4:5 B、∠A:∠B:∠C=3:4:5 C、∠A+∠B=∠C D、a:b:c=1:2:2. 已知a、b、c是三角形的三边长,若满足 , 则这个三角形的形状是( )A、等腰三角形 B、等边三角形 C、锐角三角形 D、直角三角形3. 满足下列条件的三角形中,不是直角三角形的是( )A、三内角的度数之比为1:2:3 B、三内角的度数之比为3:4:5 C、三边长之比为3:4:5 D、三边长的平方之比为1:2:34. 如果一个三角形的三边分别为1、、 , 则其面积为( )A、 B、 C、 D、5. 已知两条线段长分别为3、4,那么能与它们组成直角三角形的第三条线段长是( )A、5 B、 C、5或 D、不能确定6. 在△ABC中,已知AB=12cm,AC=9cm,BC=15cm,则△ABC的面积等于( )A、108cm2 B、90cm2 C、180cm2 D、54cm27. 三角形的三边长分别为6,8,10,那它最短边上的高为( )A、4 B、5 C、6 D、88. 有五组数:①25,7,24;②16,20,12;③9,40,41;④4,6,8;⑤32,42 , 52 , 以各组数为边长,能组成直角三角形的个数为( )A、1 B、2 C、3 D、49. △ABC的三边满足|a+b﹣16|++(c﹣8)2=0,则△ABC为( )A、直角三角形 B、 等腰三角形 C、等边三角形 D、等腰直角三角形10. △ABC中,∠A,∠B,∠C的对边分别为a,b,c,下列命题中的假命题是( )A、若∠A=∠C-∠B,则∠C=90º B、若∠C=90º,则 C、若∠A=30º,∠B=60º,则AB=2BC D、若 , 则∠C=90º
二、填空题
-
11. 四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠BAD=90°,则△BDC为三角形.
12. 已知a,b,c是直角三角形的三条边,且a<b<c,斜边上的高为h,则下列说法中正确的是 .(只填序号)①a2b2+h4=(a2+b2+1)h2;②b4+c2h2=b2c2;③由 , , 可以构成三角形;④直角三角形的面积的最大值是 .
13. 若△ABC的三边长分别为x+1,x+2,x+3,要使此三角形成为直角三角形,则x= .
14.2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽弦图它是由四全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形 的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,下列说法:
①a2+b2=13;②b2=1;③a2﹣b2=12;④ab=6.
其中正确结论序号是
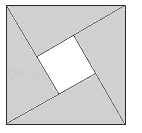 15.
15.如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC为直角三角形的点C有 个.
 16. 如图,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短的直角边长为a,较长的直角边长为b,那么(a+b)2的值为
16. 如图,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短的直角边长为a,较长的直角边长为b,那么(a+b)2的值为
三、解答题
-
17. 如图,在平面直角坐标系中,△A1B1C1与△ABC关于y轴对称.
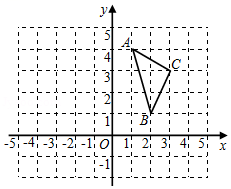 (1)、在图中画出△A1B1C1并写出点A1、B1的坐标;(2)、试判断△ABC的形状,并说明理由.18. 已知a、b、c满足(a﹣3)2++|c﹣5|=0.
(1)、在图中画出△A1B1C1并写出点A1、B1的坐标;(2)、试判断△ABC的形状,并说明理由.18. 已知a、b、c满足(a﹣3)2++|c﹣5|=0.求:(1)a、b、c的值;
(2)试问以a、b、c为边能否构成三角形?若能构成三角形,求出三角形的周长;若不能构成三角形,请说明理由.
19. 如图,在Rt△ABC中,∠BCA=90°,AC=12,AB=13,点D是Rt△ABC外一点,连接DC、DB , 且CD=4,BD=3.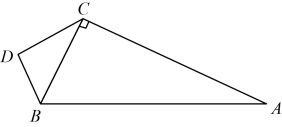 (1)、求BC的长;(2)、求证:△BCD是直角三角形.20.
(1)、求BC的长;(2)、求证:△BCD是直角三角形.20.如图,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度全速前进,2小时后甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船沿哪个方向航行吗?
 21. 在一条东西走向的河的一侧有一村庄C,河边原有两个取水点A,B,其中 , 由于某种原由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得千米,千米,千米.
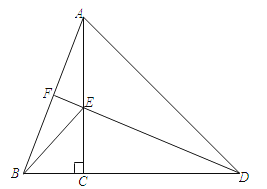
21. 在一条东西走向的河的一侧有一村庄C,河边原有两个取水点A,B,其中 , 由于某种原由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得千米,千米,千米.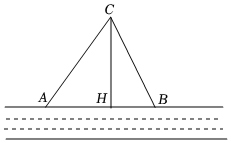 (1)、问CH是否为从村庄C到河边的最近路?请通过计算加以说明.(2)、求原来的路线AC的长.22. 如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F.
(1)、问CH是否为从村庄C到河边的最近路?请通过计算加以说明.(2)、求原来的路线AC的长.22. 如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F.(1)求证:DE⊥AB;
(2)若已知BC=a,AC=b,AB=c,设EF=x,则△ABD的面积用代数式可表示为;你能借助本题提供的图形,证明勾股定理吗?试一试吧.
 23. 综合与实践:测雕塑
23. 综合与实践:测雕塑 (1)、 如图,雕塑底座正面是四边形ABCD , 现提供一足够长的卷尺,请你设计一个方法检测雕塑底座正面的边AB是否垂直于底边BC?并说明理由.(2)、 若雕塑底座是个长方体,量得边BC长50cm,边CD长40cm,边DE长30cm,一只蚂蚁从底部点B沿雕塑的表面爬到顶部的点E , 蚂蚁爬行的最短路程是多少?24. 阅读下列一段文字,回答问题.
(1)、 如图,雕塑底座正面是四边形ABCD , 现提供一足够长的卷尺,请你设计一个方法检测雕塑底座正面的边AB是否垂直于底边BC?并说明理由.(2)、 若雕塑底座是个长方体,量得边BC长50cm,边CD长40cm,边DE长30cm,一只蚂蚁从底部点B沿雕塑的表面爬到顶部的点E , 蚂蚁爬行的最短路程是多少?24. 阅读下列一段文字,回答问题.[材料阅读]平面内两点M(x1 , y1),N(x2 , y2),则由勾股定理可得,这两点间的距离MN= .
例如,如图1,M(3,1),N(,-2),则MN= .
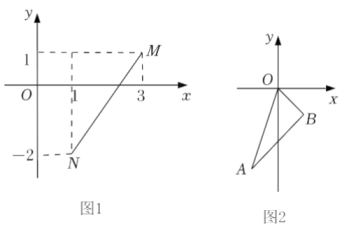
[直接应用]
(1)、已知P(2,-3),Q(-1,3), 求P、Q两点间的距离;(2)、如图2,在平面直角坐标系中,A(-1,-3),OB= , OB与x轴正半轴的夹角是45°.试判断△ABO的形状并证明.