河北省石家庄市平山县2023-2024学年九年级上学期数学第三次月考考试试卷
试卷更新日期:2024-01-05 类型:月考试卷
一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 下列图象中是反比例函数图象的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若两个相似三角形的相似比为1:4,则它们的对应高的比为( )A、1:2 B、1:4 C、1:8 D、1:163. 下面叙述中的变量与变量满足反比例函数关系的是( )
2. 若两个相似三角形的相似比为1:4,则它们的对应高的比为( )A、1:2 B、1:4 C、1:8 D、1:163. 下面叙述中的变量与变量满足反比例函数关系的是( )①计划从地到地铺设一段2400米长的铁轨,每日铺设长度与铺设天数;
②汽车匀速行驶时,行驶的路程与行驶的时间.
A、只有①是 B、只有②是 C、①②都是 D、①②都不是4. 反比例函数的图象在( )A、第一、三象限 B、第二、四象限 C、第一、二象限 D、第三、四象限5. 平行于正多边形一边的直线,把正多边形分割成两部分,则下列阴影部分与原正多边形相似的是( )A、 B、
B、 C、
C、 D、
D、 6. 已知与成反比例,当时 , 则与的函数解析式为( )A、 B、 C、 D、7. 如图, , 若 , , 则的值为( )
6. 已知与成反比例,当时 , 则与的函数解析式为( )A、 B、 C、 D、7. 如图, , 若 , , 则的值为( ) A、2:3 B、3:2 C、4:9 D、9:48. 已知点 , 在双曲线上,当时,下列结论一定正确的是( )A、 B、 C、 D、9. 如图,在由小正方形组成的方格纸中,和的顶点均在格点上,要使 , 则点所在的格点为( )
A、2:3 B、3:2 C、4:9 D、9:48. 已知点 , 在双曲线上,当时,下列结论一定正确的是( )A、 B、 C、 D、9. 如图,在由小正方形组成的方格纸中,和的顶点均在格点上,要使 , 则点所在的格点为( ) A、点 B、点 C、点 D、点10. 汽车在某高速路的限速区间段的行驶速度(km/h)与行驶时间(h)的反比例函数关系如图所示,汽车在该限速区间段的最高车速不得超过120km/h,最低车速不得低于60km/h,王先生开车按照此规定通过该限速区间段的时长可能是( )
A、点 B、点 C、点 D、点10. 汽车在某高速路的限速区间段的行驶速度(km/h)与行驶时间(h)的反比例函数关系如图所示,汽车在该限速区间段的最高车速不得超过120km/h,最低车速不得低于60km/h,王先生开车按照此规定通过该限速区间段的时长可能是( ) A、0.15h B、0.32h C、0.45h D、0.5h11. 的三个顶点的坐标分别为 , , , 以原点为位似中心,把缩小为原来的 , 可以得到 , 则点的坐标是( )A、 B、或 C、 D、或12. 西周数学家商高总结了用“矩”(如图1所示)测量物高的方法:把“矩”的两边放置成如图2所示的位置,从“矩”的一端(人眼)望点 , 使视线通过点 , 记人站立的位置为点 , 量出长,即可算得物高.若 , , , 量得 , 则物体的高为( )
A、0.15h B、0.32h C、0.45h D、0.5h11. 的三个顶点的坐标分别为 , , , 以原点为位似中心,把缩小为原来的 , 可以得到 , 则点的坐标是( )A、 B、或 C、 D、或12. 西周数学家商高总结了用“矩”(如图1所示)测量物高的方法:把“矩”的两边放置成如图2所示的位置,从“矩”的一端(人眼)望点 , 使视线通过点 , 记人站立的位置为点 , 量出长,即可算得物高.若 , , , 量得 , 则物体的高为( ) A、1.2m B、2m C、2.4m D、2.8m13. 在同一平面直角坐标系中,反比例函数与的图象如图所示,则满足条件的整数的值有( )
A、1.2m B、2m C、2.4m D、2.8m13. 在同一平面直角坐标系中,反比例函数与的图象如图所示,则满足条件的整数的值有( ) A、1个 B、2个 C、3个 D、4个14. 如图,在中,为锐角, , , 要在边上找一点 , 使 , 需添加一个条件,下列方案不正确的是( )
A、1个 B、2个 C、3个 D、4个14. 如图,在中,为锐角, , , 要在边上找一点 , 使 , 需添加一个条件,下列方案不正确的是( ) A、 B、 C、平分 D、15. 反比例函数和在第一象限内的图象如图所示,点在的图象上,过点作轴于点 , 交的图象于点 , 轴于点 , 交的图象于点.当点的横坐标逐渐变大时,四边形的面积( )
A、 B、 C、平分 D、15. 反比例函数和在第一象限内的图象如图所示,点在的图象上,过点作轴于点 , 交的图象于点 , 轴于点 , 交的图象于点.当点的横坐标逐渐变大时,四边形的面积( ) A、逐渐变大 B、逐渐变小 C、不变 D、无法确定16. 题目:“如图,在四边形中, , , , , , 是线段延长线上一点,若与相似,求的长.”嘉嘉的答案:延长交的延长线于点 , 此时 , 可得.而淇淇说:“嘉嘉考虑的不周全,还应有另一个不同的长度.”下列判断正确的是( )
A、逐渐变大 B、逐渐变小 C、不变 D、无法确定16. 题目:“如图,在四边形中, , , , , , 是线段延长线上一点,若与相似,求的长.”嘉嘉的答案:延长交的延长线于点 , 此时 , 可得.而淇淇说:“嘉嘉考虑的不周全,还应有另一个不同的长度.”下列判断正确的是( ) A、淇淇说的不对,就等于3 B、淇淇说的对,且的另一个长度为 C、嘉嘉求的结果不对,应得1.5 D、两人都不对,应有3个不同的长度
A、淇淇说的不对,就等于3 B、淇淇说的对,且的另一个长度为 C、嘉嘉求的结果不对,应得1.5 D、两人都不对,应有3个不同的长度二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分)
-
17. 某机器零件的长度为70cm,将其缩小在比例尺为1:10的图纸上的长度为cm.18. 如图,已知直线 , , 分别截直线于点 , , , 截直线于点 , , , 且.
 (1)、若 , , , 则的长为;(2)、若 , , 则的长为.19. 如图,2×2网格(每个小正方形的边长均为1)中有 , , , , , , , , 九个格点,点的坐标为 , 反比例函数的解析式为.
(1)、若 , , , 则的长为;(2)、若 , , 则的长为.19. 如图,2×2网格(每个小正方形的边长均为1)中有 , , , , , , , , 九个格点,点的坐标为 , 反比例函数的解析式为. (1)、若反比例函数的图象过点 , 则它必过点;(2)、在九个格点中,若只有1个格点在反比例函数图象的上方,则的整数值有个.
(1)、若反比例函数的图象过点 , 则它必过点;(2)、在九个格点中,若只有1个格点在反比例函数图象的上方,则的整数值有个.三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
20. 在6×6的正方形网格中,每个小正方形的边长都为1,点 , , 均在格点上.请按要求在网格中画图,所画图形的顶点均需在格点上.
 (1)、在图1中画出 , 使得与关于点位似,相似比为2;(2)、在图2中画出 , 使得 , 且.21. 已知关于的反比例函数.
(1)、在图1中画出 , 使得与关于点位似,相似比为2;(2)、在图2中画出 , 使得 , 且.21. 已知关于的反比例函数. (1)、若该函数的图象经过点 , 求的值,并在如图所示的平面直角坐标系中画出该函数的图象;(2)、当时,随的增大而减小,求的取值范围.22. 如图,在中, , 为延长线上一点, , 延长到点 , 且.
(1)、若该函数的图象经过点 , 求的值,并在如图所示的平面直角坐标系中画出该函数的图象;(2)、当时,随的增大而减小,求的取值范围.22. 如图,在中, , 为延长线上一点, , 延长到点 , 且. (1)、求证:;(2)、若 , 求的长度.23. 如图1,阳光(平行光线)通过窗户照到厂房内,竖直窗框()在地面上留下2米长的影子(),窗框影子的一端到窗下墙脚的距离为3.6米,窗口底边与地面的距离为1.2米.
(1)、求证:;(2)、若 , 求的长度.23. 如图1,阳光(平行光线)通过窗户照到厂房内,竖直窗框()在地面上留下2米长的影子(),窗框影子的一端到窗下墙脚的距离为3.6米,窗口底边与地面的距离为1.2米. (1)、求窗户的高度(的长);(2)、如图2,随着平行光线照射角度的变化,窗框影子的一端沿向右移动到 , 米,另一端恰好移动到厂房的另一墙脚 , 求的长.24. 某公司的饮水机在水温为20℃时开机加热,加热时每分钟上升20℃,加热到100℃停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,如图所示,直至水温降至20℃,饮水机关机(这是一个加热周期),饮水机关机后即刻自动开机,重复上述自动程序.
(1)、求窗户的高度(的长);(2)、如图2,随着平行光线照射角度的变化,窗框影子的一端沿向右移动到 , 米,另一端恰好移动到厂房的另一墙脚 , 求的长.24. 某公司的饮水机在水温为20℃时开机加热,加热时每分钟上升20℃,加热到100℃停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,如图所示,直至水温降至20℃,饮水机关机(这是一个加热周期),饮水机关机后即刻自动开机,重复上述自动程序. (1)、将水从20℃加热到100℃需要min;在图15中的水温下降的过程中,求水温与开机后用时的函数解析式(不写自变量的取值范围);(2)、在一个加热周期中,求水温不低于40℃的时长;(3)、王经理去接水时看到饮水机的水温刚好降到50℃,若他想接到60℃的水(在不打断加热周期的情况下),请直接写出他至少还要等待多长时间?25. 如图,直线与反比例函数的图象交于点 , , 与轴交于点 , 与轴交于点.
(1)、将水从20℃加热到100℃需要min;在图15中的水温下降的过程中,求水温与开机后用时的函数解析式(不写自变量的取值范围);(2)、在一个加热周期中,求水温不低于40℃的时长;(3)、王经理去接水时看到饮水机的水温刚好降到50℃,若他想接到60℃的水(在不打断加热周期的情况下),请直接写出他至少还要等待多长时间?25. 如图,直线与反比例函数的图象交于点 , , 与轴交于点 , 与轴交于点.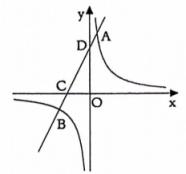 (1)、求的值和反比例函数的解析式;(2)、在轴上有一动点(),过点作平行于轴的直线,交反比例函数的图象于点 , 交直线于点 , 连接.
(1)、求的值和反比例函数的解析式;(2)、在轴上有一动点(),过点作平行于轴的直线,交反比例函数的图象于点 , 交直线于点 , 连接.①若点到轴的距离小于4,求的取值范围;
②当时,若 , 求的值.
26. 如图1,在中, , , , 点从点出发,沿折线以每秒1个单位长度的速度运动,设点的运动时间为()s. (1)、求的长;(2)、如图2,当点在上,过点作的垂线,垂足为.
(1)、求的长;(2)、如图2,当点在上,过点作的垂线,垂足为.①求证:;
②当时,求的长;
(3)、设点移动的路程为 , 当及时,分别求点到直线的距离;(用含的式子表示)(4)、过点作 , 交于点.当时,请直接写出的值.