河北省唐山市丰南区2023-2024学年九年级上学期数学期中考试试卷
试卷更新日期:2024-01-05 类型:期中考试
一、精心选一选(本大题共16小题.1-10题,每题3分;11-16题,每题2分,共42分)每小题给出的4个选项中只有一个符合题意,请将所选选项的字母代号写在题中的括号内.
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,抛物线的顶点是( )A、 B、 C、 D、3. 把一元二次方程化成一般形式,正确的是( )A、 B、 C、 D、4. 用配方法解方程 时,配方结果正确的是( ).A、 B、 C、 D、5. 设方程的两个根为 , , 那么的值等于( )A、-2 B、1 C、-1 D、26. 将向左平移3个单位,再向上平移3个单位,得到的抛物线为( )A、 B、 C、 D、7. 某纪念品原价168元,连续两次降价后售价为128元;下列所列方程正确的是( )A、 B、 C、 D、8. 二次函数的部分对应值如表则一元二次方程的解为( )
2. 在平面直角坐标系中,抛物线的顶点是( )A、 B、 C、 D、3. 把一元二次方程化成一般形式,正确的是( )A、 B、 C、 D、4. 用配方法解方程 时,配方结果正确的是( ).A、 B、 C、 D、5. 设方程的两个根为 , , 那么的值等于( )A、-2 B、1 C、-1 D、26. 将向左平移3个单位,再向上平移3个单位,得到的抛物线为( )A、 B、 C、 D、7. 某纪念品原价168元,连续两次降价后售价为128元;下列所列方程正确的是( )A、 B、 C、 D、8. 二次函数的部分对应值如表则一元二次方程的解为( ).…
-2
-1
0
1
2
4
…
…
5
0
-3
-4
-3
5
…
A、 , B、 , C、 , D、 ,9. 如图,一块长方形绿地的长为 , 宽为 , 在绿地中开辟两条道路后剩余绿地面积为 , 则根据题意可列出方程( ) A、 B、 C、 D、10. 如图,将矩形绕点顺时针旋转到矩形的位置,旋转角为.若 , 则( )
A、 B、 C、 D、10. 如图,将矩形绕点顺时针旋转到矩形的位置,旋转角为.若 , 则( ) A、20° B、30° C、40° D、50°11. 若 , , 为二次函数的图象上的三点,则 , , 的大小关系是( )A、 B、 C、 D、12. 已知二次函数的图象如图所示,对称轴为 , 下列结论中正确的是( )
A、20° B、30° C、40° D、50°11. 若 , , 为二次函数的图象上的三点,则 , , 的大小关系是( )A、 B、 C、 D、12. 已知二次函数的图象如图所示,对称轴为 , 下列结论中正确的是( ) A、 B、 C、 D、13. 如图,的正方形网格中,绕某点旋转一定的角度,得到 , 其旋转中心是( )
A、 B、 C、 D、13. 如图,的正方形网格中,绕某点旋转一定的角度,得到 , 其旋转中心是( ) A、点 B、点 C、点 D、点14. 在同一平面直角坐标系中,一次函数 与二次函数 的图象可能是( )A、
A、点 B、点 C、点 D、点14. 在同一平面直角坐标系中,一次函数 与二次函数 的图象可能是( )A、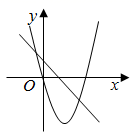 B、
B、 C、
C、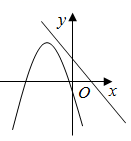 D、
D、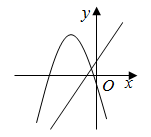 15. 已知关于的方程的一个根是2,且二次函数的对称轴是直线 , 则这条拋物线的顶点坐标为( )A、 B、 C、 D、16. 已知一次函数和二次函数部分自变量和对应的函数值如下表:当时,自变量的取值范围是( )
15. 已知关于的方程的一个根是2,且二次函数的对称轴是直线 , 则这条拋物线的顶点坐标为( )A、 B、 C、 D、16. 已知一次函数和二次函数部分自变量和对应的函数值如下表:当时,自变量的取值范围是( )…
-1
0
2
4
5
…
…
0
1
3
5
6
…
…
0
-1
0
5
9
…
A、 B、 C、或 D、或二、细心填一填(本大题共4小题,共12分)把答案直接写在题中的横线上.
-
17. 一元二次方程 的根是.18. 九年级(3)班文学小组在举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,全组共互赠了240本图书.如果设全组共有名同学,依题意,可列出的方程是.19. 若二次函数y=x2+2x+m的图象与坐标轴有3个交点,则m的取值范围是.20. 如图,线段的两个顶点都在方格纸的格点上,建立平面直角坐标系后,、的坐标分别是 , , 将线段绕点顺时针旋转90°后得到.则点关于原点的对称点的坐标是.

三、专心解一解(本题满分66分)请认真读题,冷静思考.解答题应写出文字说明、解答过程.
-
21. 已知、是关于的一元二次方程的两个实数根,且(在A,B中任选一个条件解答下列问题)
A:
B:
(1)、求的值:(2)、解此方程.22. 在如图所示的平面直角坐标系中(每个小方格都是边长为1个单位长度的正方形),解答下列问题: (1)、画出与关于轴对称的;(2)、画出以为旋转中心,将顺时针旋转90°后的;(3)、连接 , 则是三角形,的面积是.23. 如图,已知二次函数图象经过点和点.
(1)、画出与关于轴对称的;(2)、画出以为旋转中心,将顺时针旋转90°后的;(3)、连接 , 则是三角形,的面积是.23. 如图,已知二次函数图象经过点和点. (1)、求该二次函数的解析式;(2)、结合函数图象,直接回答下列问题:
(1)、求该二次函数的解析式;(2)、结合函数图象,直接回答下列问题:①当时,函数的取值范围:.
②当时,的取值范围:.
③方程的解为:.
24. 某商品交易会上,一店铺将每件进价为5元的纪念品,按每件9元出售,每天可售出32件.该店铺想采用提高售价的办法来增加利润,经试验,发现这种纪念品每件提价1元,每天的销售量会减少4件.(1)、当售价定为多少元时,每天的利润为140元?(2)、商人为了获得最大利润,应将该商品每件售价定为多少元?最大利润是多少元?25. 如图1,是等边三角形.内一点,连接 , , , 且 , , 将绕点顺时针旋转后得到 , 连接. (1)、 填空:①旋转角为°;②线段的长是;③°;(2)、如图2,是内一点,且 , .连接 , , , 将绕点顺时针旋转后得到 , 连接.当 , , 满足什么条件时,?请说明理由.26. 如图,抛物线经过点 , , 与轴正半轴交于点 , 且 , 抛物线的顶点为 , 对称轴交轴于点.直线经过 , 两点.
(1)、 填空:①旋转角为°;②线段的长是;③°;(2)、如图2,是内一点,且 , .连接 , , , 将绕点顺时针旋转后得到 , 连接.当 , , 满足什么条件时,?请说明理由.26. 如图,抛物线经过点 , , 与轴正半轴交于点 , 且 , 抛物线的顶点为 , 对称轴交轴于点.直线经过 , 两点. (1)、求拋物线及直线的函数表达式;(2)、点是抛物线对称轴上一点,当的值最小时,求出点的坐标及的最小值;(3)、若点是抛物线对称轴上一点,试探究是否存在以点为直角顶点的 , 若存在,求出点的坐标;若不存在,请说明理由.
(1)、求拋物线及直线的函数表达式;(2)、点是抛物线对称轴上一点,当的值最小时,求出点的坐标及的最小值;(3)、若点是抛物线对称轴上一点,试探究是否存在以点为直角顶点的 , 若存在,求出点的坐标;若不存在,请说明理由.