河北省保定市清苑区2023-2024学年七年级上学期数学期中考试试卷
试卷更新日期:2024-01-05 类型:期中考试
一、选择题(本大题共16个小题,共38分.1∼6小题各3分,7∼16小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
-
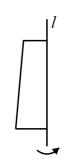
1. 的倒数是( )A、 B、 C、 D、2. 将下方如图所示的直角梯形绕直线旋转一周,得到的立体图形是( )
 A、
A、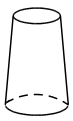 B、
B、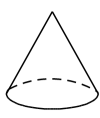 C、
C、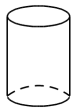 D、
D、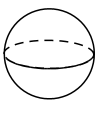 3. 一个物体做左右方向的运动,若规定向右运动记作 , 则向左运动记作( )A、 B、 C、 D、4. 下列有理数的大小关系中,正确的是( )A、 B、 C、 D、5. 如图,数轴上点A与点的距离为( )
3. 一个物体做左右方向的运动,若规定向右运动记作 , 则向左运动记作( )A、 B、 C、 D、4. 下列有理数的大小关系中,正确的是( )A、 B、 C、 D、5. 如图,数轴上点A与点的距离为( ) A、 B、1 C、2 D、36. 如图,这是一个几何体的侧面展开图,则该几何体的形状是( )
A、 B、1 C、2 D、36. 如图,这是一个几何体的侧面展开图,则该几何体的形状是( )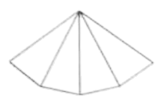 A、四棱柱 B、四棱锥 C、五棱柱 D、五棱锥7. 下列运算结果等于1的是( )A、 B、 C、 D、8. 下列判断正确的是( )A、的系数是2 B、的次数是2 C、的系数是 D、3不是单项式9. 某科研团队研制的一种新型材料,在一定条件下具有自主伸长的功能,每秒伸长2纳米,则4小时该材料伸长( )A、纳米 B、纳米 C、纳米 D、纳米10. 若n表示一个奇数,则下面各数中表示偶数的是( )A、 B、 C、 D、11. 若单项式与的和仍是单项式,则的值是( )A、3 B、8 C、9 D、1612. 已知 , , 且 , 则的值等于( )A、1或 B、5或 C、或 D、5或113. 有理数 , 在数轴上的对应点如图所示,则下列式子正确的是( )
A、四棱柱 B、四棱锥 C、五棱柱 D、五棱锥7. 下列运算结果等于1的是( )A、 B、 C、 D、8. 下列判断正确的是( )A、的系数是2 B、的次数是2 C、的系数是 D、3不是单项式9. 某科研团队研制的一种新型材料,在一定条件下具有自主伸长的功能,每秒伸长2纳米,则4小时该材料伸长( )A、纳米 B、纳米 C、纳米 D、纳米10. 若n表示一个奇数,则下面各数中表示偶数的是( )A、 B、 C、 D、11. 若单项式与的和仍是单项式,则的值是( )A、3 B、8 C、9 D、1612. 已知 , , 且 , 则的值等于( )A、1或 B、5或 C、或 D、5或113. 有理数 , 在数轴上的对应点如图所示,则下列式子正确的是( )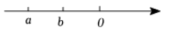 A、 B、 C、 D、14. 课堂上丁老师带来一个立体图形的模型,嘉嘉同学从某一角度看到的形状为三角形,则这一立体图形一定不是( )A、圆柱 B、圆锥 C、棱柱 D、棱锥15. 某网络销售平台举行9月新学期“优惠”季,宣传如下,则横线处应是下列说法中的( )
A、 B、 C、 D、14. 课堂上丁老师带来一个立体图形的模型,嘉嘉同学从某一角度看到的形状为三角形,则这一立体图形一定不是( )A、圆柱 B、圆锥 C、棱柱 D、棱锥15. 某网络销售平台举行9月新学期“优惠”季,宣传如下,则横线处应是下列说法中的( )“开学季,低价风暴”活动来袭!
原售价:元.
优惠方案:
优惠价(现售价):元.
A、原售价基础上减90元,再打七折 B、原售价基础上减90元,再打三折 C、原售价基础上打七折,再减90元 D、原售价基础上打三折,再减90元16. 已知代数式 , , 若的值与的取值无关,则的值为( )A、3 B、2 C、1 D、0二、填空题(本大题共3个小题,共10分.17小题2分,18∼19小题各4分,每空2分)
-
17. 已知正方体的一个平面展开图如图所示,则在原正方体上,“创”的对立面的汉字是 .
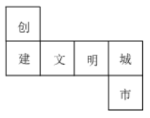 18. 数轴上一点从原点向数轴正方向移动2个单位长度,此时点表示的数为;另一点移动3个单位长度后到达原点处,则点移动前表示的数为 .19. 践行环保,人人有责,向阳中学七年级(1)班的同学利用课后活动时间收集旧电池,下面是嘉嘉同学和琪琪同学的对话,根据对话完成相关问题.
18. 数轴上一点从原点向数轴正方向移动2个单位长度,此时点表示的数为;另一点移动3个单位长度后到达原点处,则点移动前表示的数为 .19. 践行环保,人人有责,向阳中学七年级(1)班的同学利用课后活动时间收集旧电池,下面是嘉嘉同学和琪琪同学的对话,根据对话完成相关问题.嘉嘉:“你再收集两节旧电池,你的电池数量就是我的电池数量的两倍了!”
琪琪:“是的,我这里太多了,给你两节旧电池吧!”
(1)、若嘉嘉收集了节电池,则琪琪收集了节电池.(用含的代数式表示)(2)、在(1)的条件下,琪琪给了嘉嘉之后,还比嘉嘉多节电池.(用含的代数式表示)三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
20. 计算:(1)、 .(2)、 .21. 先化简,再求值: , 其中 , .22. 如图,是由5个大小相同的小立方体搭建的几何体,其中每个小正方体的棱长为1厘米.
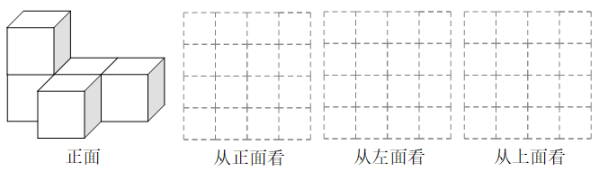 (1)、直接写出这个几何体的表面积: .(2)、请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.23. 定义新运算: .(1)、求的值.(2)、求的值.24. 如图1,该三棱柱的高为 , 底面是一个每条边长都为的三角形.
(1)、直接写出这个几何体的表面积: .(2)、请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图.23. 定义新运算: .(1)、求的值.(2)、求的值.24. 如图1,该三棱柱的高为 , 底面是一个每条边长都为的三角形.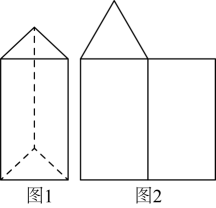 (1)、这个三棱柱有个面,有条棱.(2)、如图2,这是该三棱柱的表面展开图的一部分,请将它补充完整.(3)、这个三棱柱的侧面积是 , 要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最大值为 .25. 如图,这是某种磁力飞镖靶盘,小欣和小强各玩一局,每局投掷10次飞镖.若飞镖投到边界线上,则不计入次数,重新投掷飞镖.图1是小欣10次投掷飞镖的情况(黑点为飞镖被投掷的位置),且各区域计分如下表.
(1)、这个三棱柱有个面,有条棱.(2)、如图2,这是该三棱柱的表面展开图的一部分,请将它补充完整.(3)、这个三棱柱的侧面积是 , 要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最大值为 .25. 如图,这是某种磁力飞镖靶盘,小欣和小强各玩一局,每局投掷10次飞镖.若飞镖投到边界线上,则不计入次数,重新投掷飞镖.图1是小欣10次投掷飞镖的情况(黑点为飞镖被投掷的位置),且各区域计分如下表.投中位置
区
区
脱靶
一次计分/分
3
1
-2
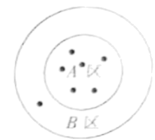 (1)、请计算小欣的最终得分.(2)、若小强投中区3次,区次.
(1)、请计算小欣的最终得分.(2)、若小强投中区3次,区次.①求小强的最终得分.(用含的代数式表示)
②请判断小强的分数有没有可能超过小欣的分数,并说明理由.
26. 向阳中学为增强学生身体素质,增加校园体育文化氛围,举行师生踢毽子比赛.七年级(1)班42人参加比赛,预赛成绩统计如下(踢毽子标准数量为20个).踢建子个数与标准数量的差值
人数
(1)、表中的值为 .(2)、求七年级(1)班42人平均每人踢毽子多少个?(3)、规定踢毽子达到标准数量记0分;踢毽子超过标准数量,每多踢1个加2分;踢毽子未达到标准数量,每少踢1个,扣1分.若班级总分数达到270分可进入决赛,请通过计算判断七年级(1)班能否进入决赛.