河北省邢台市襄都区邢台英华教育集团2023-2024学年九年级上学期数学月考考试试卷(12月)
试卷更新日期:2024-01-05 类型:月考试卷
一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
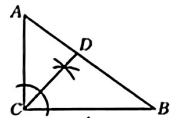
1. 已知的半径为6cm,点到直线的距离为7cm,则直线与的位置关系是( )A、相离 B、相切 C、相交 D、无法确定2. 下列关于的函数中,一定是二次函数的是( )A、 B、 C、 D、3. 在中, , , , 则等于( )A、 B、 C、 D、4. 在一次体育测试中,嘉琪所在小组6人的成绩分别是:46,47,47,49,49,49.则这6人体育测试成绩的中位数是( )A、47 B、48 C、 D、495. 设一元二次方程的两根分别是 , , 且满足 , 则的值为( )A、1 B、2 C、 D、6. 在中, , 用直尺和圆规在边上确定一点 , 使 , 根据作图痕迹判断,下列正确的是( )A、
 B、
B、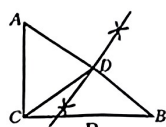 C、
C、 D、
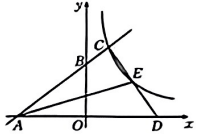
D、 7. 如图,在中,弦、相交于点 , , , 则( )
7. 如图,在中,弦、相交于点 , , , 则( ) A、 B、 C、 D、8. 如图,点在反比例函数的图像上,轴,垂足为 , 轴,垂足为 . 为的中点,为的中点,若矩形的面积为3,则的值为( )
A、 B、 C、 D、8. 如图,点在反比例函数的图像上,轴,垂足为 , 轴,垂足为 . 为的中点,为的中点,若矩形的面积为3,则的值为( )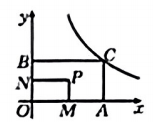 A、3 B、6 C、9 D、129. 如图,有四个二次函数的图象,分别对应的函数解析式是:①;②;③;④ . 则 , , , 的大小关系是( )
A、3 B、6 C、9 D、129. 如图,有四个二次函数的图象,分别对应的函数解析式是:①;②;③;④ . 则 , , , 的大小关系是( )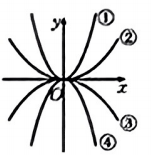 A、 B、 C、 D、10. 已知一个三角形的内心与外心重合,若它的内切圆的半径为2,则它的外接圆的面积为( )A、 B、 C、 D、11. 如图,、、、为一个正多边形的四个顶点,点为这个正多边形的中心.若 , 则这个正多边形的边数为( )
A、 B、 C、 D、10. 已知一个三角形的内心与外心重合,若它的内切圆的半径为2,则它的外接圆的面积为( )A、 B、 C、 D、11. 如图,、、、为一个正多边形的四个顶点,点为这个正多边形的中心.若 , 则这个正多边形的边数为( )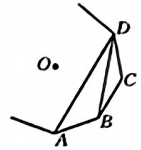 A、7 B、8 C、9 D、1012. 将抛物线向左平移3个单位长度,再向下平移6个单位长度,得到抛物线的解析式为( )A、 B、 C、 D、13. 如图,的圆心在梯形的底边上,且与梯形的其他三边均相切,若 , , 则梯形的周长为( )
A、7 B、8 C、9 D、1012. 将抛物线向左平移3个单位长度,再向下平移6个单位长度,得到抛物线的解析式为( )A、 B、 C、 D、13. 如图,的圆心在梯形的底边上,且与梯形的其他三边均相切,若 , , 则梯形的周长为( ) A、8 B、10 C、14 D、1814. 如图,正六边形内接于 , 的半径为6,则这个正六边形的边心距和的长分别为( )
A、8 B、10 C、14 D、1814. 如图,正六边形内接于 , 的半径为6,则这个正六边形的边心距和的长分别为( ) A、3, B、 , C、 , D、 ,15. 如图,四边形是菱形,边长为 , . 点从点出发,沿方向以每秒个单位长度的速度运动,同时点沿射线的方向以每秒1个单位长度的速度运动,当点运动到达点时,点也立刻停止运动,连接 . 的面积为 , 点运动的时间为秒,则能大致反映与之间的函数关系的图像是( )
A、3, B、 , C、 , D、 ,15. 如图,四边形是菱形,边长为 , . 点从点出发,沿方向以每秒个单位长度的速度运动,同时点沿射线的方向以每秒1个单位长度的速度运动,当点运动到达点时,点也立刻停止运动,连接 . 的面积为 , 点运动的时间为秒,则能大致反映与之间的函数关系的图像是( )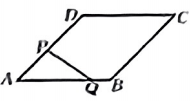 A、
A、 B、
B、 C、
C、 D、
D、 16. 二次函数的图像如图所示.下列结论正确的有( )
16. 二次函数的图像如图所示.下列结论正确的有( )
①;②;③为任意实数时,;④;⑤若 , 且;则 .
A、1个 B、2个 C、3个 D、4个二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分)
-
17. 如图,在中.、分别是、上的点, , 且 . 则 .
 18. 在平面直角坐标系中,抛物线的顶点坐标为 , 若抛物线与轴相交于 , 两点,则 . .19. 如图,在中. , . 是的内切圆.分别与 , , 相切于点 , , .
18. 在平面直角坐标系中,抛物线的顶点坐标为 , 若抛物线与轴相交于 , 两点,则 . .19. 如图,在中. , . 是的内切圆.分别与 , , 相切于点 , , . (1)、 .(2)、若 , 则 .
(1)、 .(2)、若 , 则 .三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
20. 已知抛物线 . 抛物线上 , 两点的横坐标满足 .(1)、这条抛物线的对称轴是 , 顶点坐标是 .(2)、比较 , 的大小.21. 2023年7月5日,星际荣耀“双曲线二号”验证火箭动力系统试车取得圆满成功.为了庆祝这个时刻,某县举办了科技知识活动,根据综合成绩选择一位同学参加市活动.已知嘉嘉与琪琪进入前两名,她们的各项成绩(单项满分100分)如下表所示:
选手
征文
演讲
歌唱
嘉嘉
75分
90分
87分
琪琪
84分
83分
88分
(1)、如果把各项成绩的平均分作为综合成绩,应推选谁?(2)、如果把征文、演讲、歌唱三项成绩按的比例作为综合成绩,应推选谁?22. 网络直播销售已经成为一种热门的销售方式,某商家在一销售平台上进行直播销售苹果.已知苹果的成本价为6元/千克,如果按10元/千克的售价进行销售,每天可卖出160千克.通过调查发现,苹果每千克售价每增加1元,日销售量减少20千克.(1)、为保证每天利润为700元,商家又想尽快减少库存,则苹果每千克售价应为多少元?(2)、苹果每千克售价为多少元时,每天的销售利润最大,最大利润是多少?23. 如图,已知为的直径,是的中点,垂直于过点的直线于点 .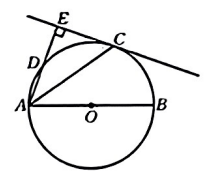 (1)、求证:是的切线.(2)、若 , . 求的长.24. 如图,正方形内接于 , 的半径为 , 是上的一个动点,连接 , , 分别交于点 , .
(1)、求证:是的切线.(2)、若 , . 求的长.24. 如图,正方形内接于 , 的半径为 , 是上的一个动点,连接 , , 分别交于点 , .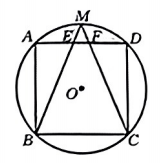 (1)、求的度数.(2)、若 , 求的长.
(1)、求的度数.(2)、若 , 求的长.