北师大版数学八年级上册期末冲刺满分攻略1 勾股定理
试卷更新日期:2024-01-04 类型:复习试卷
一、选择题
-
1. 下列各组数中,以它们为边长的线段能构成直角三角形的是( )A、4,12,13 B、3,4, C、9,12,15 D、5,11,122. 已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件中不能判断△ABC是直角三角形的是( )A、∠A=∠C-∠B B、a2=b2-c2 C、a=3,b=5,c=4 D、a:b:c=2:3:43. 一个直角三角形的两直角边长分别为5和12,则它斜边上的高长为( )A、13 B、 C、 D、4. 如图,阴影部分表示以Rt△ABC的各边为直径的三个半圆所组成的两个新月形,面积分别记作S1和S2 . 若AC=6,BC=8,则阴影部分面积S1+S2是( )
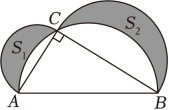 A、9π B、12.5π C、14 D、245. 如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼接成的大正方形,若直角三角形的两条直角边长分别为a , b(a>b),大正方形的面积为S1 , 小正方形的面积为S2 , 则用含S1 , S2的代数式表示(a+b)2正确的是( )
A、9π B、12.5π C、14 D、245. 如图,“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼接成的大正方形,若直角三角形的两条直角边长分别为a , b(a>b),大正方形的面积为S1 , 小正方形的面积为S2 , 则用含S1 , S2的代数式表示(a+b)2正确的是( )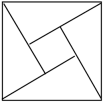 A、S1 B、S2 C、2S1-S2 D、2S2-S16. 如图,数轴上点A对应的数是0,点C对应的数是-4,BC⊥AC , 垂足为C , 且BC=1,以点A为圆心,AB长为半径画弧,交数轴于点D , 则点D表示的数为( )
A、S1 B、S2 C、2S1-S2 D、2S2-S16. 如图,数轴上点A对应的数是0,点C对应的数是-4,BC⊥AC , 垂足为C , 且BC=1,以点A为圆心,AB长为半径画弧,交数轴于点D , 则点D表示的数为( ) A、- B、 C、-4.2 D、-4.57. 如图,直线l过等腰直角三角形顶点B , 其中点A到直线l的距离是2,AC长 , 则点C到直线l的距离是( )
A、- B、 C、-4.2 D、-4.57. 如图,直线l过等腰直角三角形顶点B , 其中点A到直线l的距离是2,AC长 , 则点C到直线l的距离是( )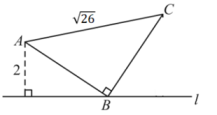 A、 B、 C、 D、38. 图中字母所代表的正方形面积为175的是( )A、
A、 B、 C、 D、38. 图中字母所代表的正方形面积为175的是( )A、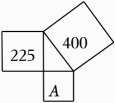 B、
B、 C、
C、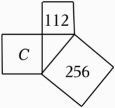 D、
D、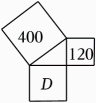 9. 如图,在中, , , , Q是上一动点,过点Q作于M , 于N , , 则的长是( )
9. 如图,在中, , , , Q是上一动点,过点Q作于M , 于N , , 则的长是( )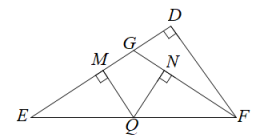 A、 B、 C、4 D、10. 如图,在平面直角坐标系中,已知点O(0,0),A(2,3),以点O为圆心,OA长为半径画弧,交x轴的正半轴于B点,则B点的横坐标介于( )
A、 B、 C、4 D、10. 如图,在平面直角坐标系中,已知点O(0,0),A(2,3),以点O为圆心,OA长为半径画弧,交x轴的正半轴于B点,则B点的横坐标介于( )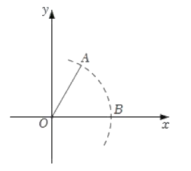 A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间
A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间二、填空题
-
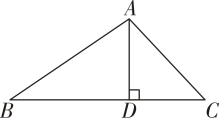
11. 如图,在△ABC中,AB=15,AC=9 , AD⊥BC于D,∠ACB=45°,则BC的长为 .
 12. 如图,在 中, , ,点 与数轴上表示1的点重合,点 与数轴上表示2的点重合,以 为圆心, 长为半径画圆弧,与数轴交于点 ,则点 所表示的数是 .
12. 如图,在 中, , ,点 与数轴上表示1的点重合,点 与数轴上表示2的点重合,以 为圆心, 长为半径画圆弧,与数轴交于点 ,则点 所表示的数是 .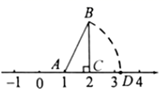 13.
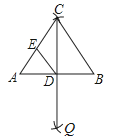
13.如图,已知线段AB,分别以A、B为圆心,大于AB长为半径画弧,两弧相交于点C、Q,连接CQ与AB相交于点D,连接AC,BC,E为AC的中点,连接DE,当线段AB=4,∠ACB=60°时,△CED周长是
 14.
14.我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).如图2由弦图变化得到,它是用八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1 , S2 , S3 , 若S1+S2+S3=20,则S2的值是
 15.
15.如图是我国古代数学家赵爽在为《周髀算经》作注解时给出的“弦图”,它解决的数学问题是
 16.
16.如图所示,在一张长为4cm、宽为3cm的矩形纸片上,现要剪下一个腰长2cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,另两个顶点在矩形的边上),则剪下的等腰三角形面积为

三、作图题
-
17. 如图,在的正方形网格中,每个小格的顶点叫做格点,每一个小正方形的边长都是1,以格点为顶点的三角形叫做格点三角形,分别按下列要求作图.
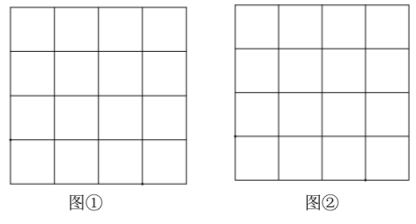 (1)、在图①中,画一个格点三角形 , 使得;(2)、在(1)的条件下,直接写出边上的高;(3)、在图②中,画一个直角三角形,使它的三边长都是无理数.18. 将一长方形纸片ABCD折叠,使顶点A与C重合,折痕为EF.
(1)、在图①中,画一个格点三角形 , 使得;(2)、在(1)的条件下,直接写出边上的高;(3)、在图②中,画一个直角三角形,使它的三边长都是无理数.18. 将一长方形纸片ABCD折叠,使顶点A与C重合,折痕为EF.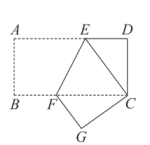 (1)、试说明CE=CF;(2)、若AB=4,BC=8,求DE的长.19. 阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为: 其中m>n>0,m,n是互质的奇数.
(1)、试说明CE=CF;(2)、若AB=4,BC=8,求DE的长.19. 阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为: 其中m>n>0,m,n是互质的奇数.应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
20. 小明和同桌小聪在课后复习时,对练习册“目标与评定”中的一道思考题,进行了认真地探索.(思考题)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米? 21. 已知:如图,有一块的绿地,量得两直角边m, , 现要将这块绿地扩充成等腰 , 且扩充部分()是以8m为直角边长的直角三角形,求扩充后等腰△ABD的周长.
21. 已知:如图,有一块的绿地,量得两直角边m, , 现要将这块绿地扩充成等腰 , 且扩充部分()是以8m为直角边长的直角三角形,求扩充后等腰△ABD的周长. (1)、在图1中,当m时,的周长为;(2)、在图2中,当m时,的周长为;(3)、在图3中,当时,求的周长.22. 如图,△ABC中,AC=BC,直线l进过点C(点A,B都在直线l的同侧),AD⊥l,BE⊥l,E,垂足分别为点D,且AD=CE=6,DC=8,AC=10.
(1)、在图1中,当m时,的周长为;(2)、在图2中,当m时,的周长为;(3)、在图3中,当时,求的周长.22. 如图,△ABC中,AC=BC,直线l进过点C(点A,B都在直线l的同侧),AD⊥l,BE⊥l,E,垂足分别为点D,且AD=CE=6,DC=8,AC=10.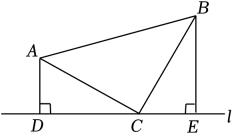 (1)、求证:△ADC≌△CEB;(2)、求△ACB的面积.23. 如图(1),平面内有四个点,它们的坐标分别是O(0,0),A(3,0),B(3,2),C(0,2).
(1)、求证:△ADC≌△CEB;(2)、求△ACB的面积.23. 如图(1),平面内有四个点,它们的坐标分别是O(0,0),A(3,0),B(3,2),C(0,2).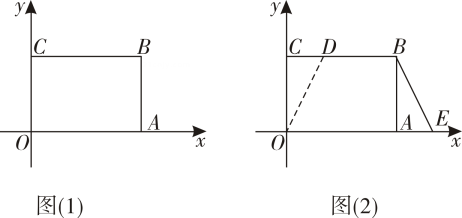 (1)、以O,A,B,C四点为顶点的四边形是一个什么图形?(2)、若点D的坐标为(1,2),将四边形OABC沿OD剪下△OCD,并拼成如图(2)所示的图形,求点E的坐标,并求出四边形OEBD的面积.(3)、在图(2)中,如果连接OB,DE,那么OB与DE是否相等?请通过计算说明理由.24. 学完勾股定理的证明后发现运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为等面积法.
(1)、以O,A,B,C四点为顶点的四边形是一个什么图形?(2)、若点D的坐标为(1,2),将四边形OABC沿OD剪下△OCD,并拼成如图(2)所示的图形,求点E的坐标,并求出四边形OEBD的面积.(3)、在图(2)中,如果连接OB,DE,那么OB与DE是否相等?请通过计算说明理由.24. 学完勾股定理的证明后发现运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为等面积法.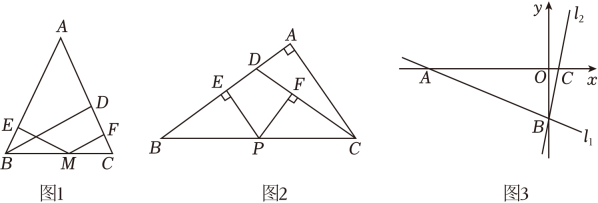 (1)、【学有所用】如图1,在等腰△ABC中,AB=AC , 其一腰上的高BD为h , M是底边BC上的任意一点,M到腰AB、AC的距离ME、MF分别为h1、h2 , 小明发现,通过连接AM , 将△ABC的面积转化为△ABM和△ACM的面积之和,建立等量关系,便可证明h1+h2=h , 请你结合图形来证明:h1+h2=h;(2)、【尝试提升】如图2,在△ABC中,∠A=90°,D是AB边上一点,使BD=CD , 过BC上一点P , 作PE⊥AB , 垂足为点E , 作PF⊥CD , 垂足为点F , 已知AB=6 , BC=6 , 求PE+PF的长.(3)、【拓展迁移】如图3,在平面直角坐标系中有两条直线l1:y=-x-5,l2:y=5x-5,若l2上的一点M到l1的距离是2,求的值.
(1)、【学有所用】如图1,在等腰△ABC中,AB=AC , 其一腰上的高BD为h , M是底边BC上的任意一点,M到腰AB、AC的距离ME、MF分别为h1、h2 , 小明发现,通过连接AM , 将△ABC的面积转化为△ABM和△ACM的面积之和,建立等量关系,便可证明h1+h2=h , 请你结合图形来证明:h1+h2=h;(2)、【尝试提升】如图2,在△ABC中,∠A=90°,D是AB边上一点,使BD=CD , 过BC上一点P , 作PE⊥AB , 垂足为点E , 作PF⊥CD , 垂足为点F , 已知AB=6 , BC=6 , 求PE+PF的长.(3)、【拓展迁移】如图3,在平面直角坐标系中有两条直线l1:y=-x-5,l2:y=5x-5,若l2上的一点M到l1的距离是2,求的值.