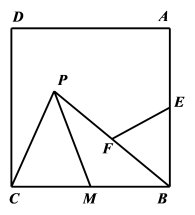2023~2024学年中考数学重难点突破之圆动点相关题型
试卷更新日期:2024-01-04 类型:三轮冲刺
一、线圆最值(定弦定角)
-
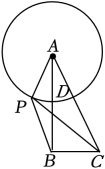
1. 如图,在Rt△ABC中,AB⊥BC,AB=6,BC=4.P是△ABC内部的一个动点,且满足∠PAB=∠PBC ,则线段CP长的最小值为
 2. 如图,正方形中, , E为边上一动点,连接 , 过点B作于F,连接 , 则的最小值为 .
2. 如图,正方形中, , E为边上一动点,连接 , 过点B作于F,连接 , 则的最小值为 . 3. 如图,在正方形ABCD中,AB=4,E是对角线BD的中点,点F为BC所在直线上方一点,连接BF、CF、EF , 若∠BFC=30°,则EF长的最大值为 .
3. 如图,在正方形ABCD中,AB=4,E是对角线BD的中点,点F为BC所在直线上方一点,连接BF、CF、EF , 若∠BFC=30°,则EF长的最大值为 .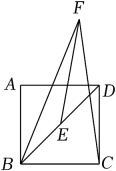 4. 如图所示,为矩形中边上的一点,已知 , , 若点在矩形内部,且 , 则的最小值为 .
4. 如图所示,为矩形中边上的一点,已知 , , 若点在矩形内部,且 , 则的最小值为 .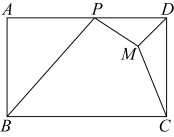 5. 如图, , , 点 , 分别在 , 的另一边上运动,并保持2,点在边上, , 点是的中点,若点为上任意一点,则的最小值为( )
5. 如图, , , 点 , 分别在 , 的另一边上运动,并保持2,点在边上, , 点是的中点,若点为上任意一点,则的最小值为( ) A、 B、 C、 D、6. 如图,点G是内的一点,且 , 是等边三角形,若 , 则的最大值为 .
A、 B、 C、 D、6. 如图,点G是内的一点,且 , 是等边三角形,若 , 则的最大值为 .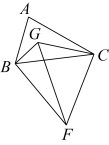 7. 如图,分别是半圆O的直径和弦, , , D是上的一个动点,连接AD.过点C作于E,连接 , 则的最小值是( )
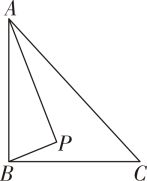
7. 如图,分别是半圆O的直径和弦, , , D是上的一个动点,连接AD.过点C作于E,连接 , 则的最小值是( )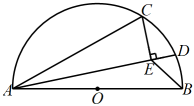 A、 B、 C、2 D、38. 如图,直角 中, ,AC=8, ,点 是 内部一动点,总满足∠APC=150°,连接 ,则 的最小值为( )
A、 B、 C、2 D、38. 如图,直角 中, ,AC=8, ,点 是 内部一动点,总满足∠APC=150°,连接 ,则 的最小值为( )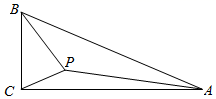 A、 B、 C、 D、9. 如图,在矩形ABCD中,E、F分别在BC、CD上运动(不与端点重合),连接BF、AE,交于点P,且满足 . 连接CP,若AB=4,BC=6,则CP的最小值为 ( )
A、 B、 C、 D、9. 如图,在矩形ABCD中,E、F分别在BC、CD上运动(不与端点重合),连接BF、AE,交于点P,且满足 . 连接CP,若AB=4,BC=6,则CP的最小值为 ( )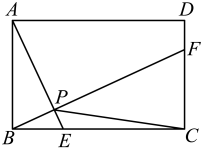 A、2-3 B、2-2 C、5 D、310. 如图,在 中, , , ,点 在边 上,且 ,点E为射线 上一动点,连接 .将 沿直线 折叠,使点C落在点P处,连接 , ,则 的面积最小值为( )
A、2-3 B、2-2 C、5 D、310. 如图,在 中, , , ,点 在边 上,且 ,点E为射线 上一动点,连接 .将 沿直线 折叠,使点C落在点P处,连接 , ,则 的面积最小值为( )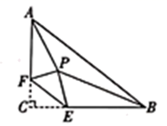 A、3 B、6 C、 D、1211. 如图,在矩形纸片ABCD中, , , 点E是AB的中点,点F是AD边上的一个动点,将沿EF所在直线翻折,得到 , 则的长的最小值是
A、3 B、6 C、 D、1211. 如图,在矩形纸片ABCD中, , , 点E是AB的中点,点F是AD边上的一个动点,将沿EF所在直线翻折,得到 , 则的长的最小值是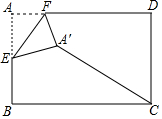 A、 B、3 C、 D、12. 如图,矩形中, , , 点、分别是线段 , 上的动点,且 , 过作的垂线,垂足为 .
A、 B、3 C、 D、12. 如图,矩形中, , , 点、分别是线段 , 上的动点,且 , 过作的垂线,垂足为 . (1)、当时,(2)、当在上运动时,的最小值为 .13. 如图,抛物线与x轴交于点 .
(1)、当时,(2)、当在上运动时,的最小值为 .13. 如图,抛物线与x轴交于点 .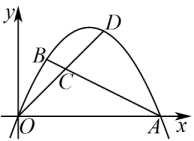
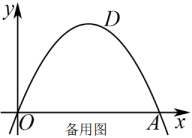 (1)、求抛物线的函数表达式;(2)、点是抛物线上一点,点C是线段上一点,连接并延长交抛物线于点D , 若 , 求点D的坐标;(3)、抛物线上是否存在点P , 使得?若存在,求出点P的坐标:若不存在,说明理由.
(1)、求抛物线的函数表达式;(2)、点是抛物线上一点,点C是线段上一点,连接并延长交抛物线于点D , 若 , 求点D的坐标;(3)、抛物线上是否存在点P , 使得?若存在,求出点P的坐标:若不存在,说明理由.二、瓜豆原理(种瓜得瓜,种豆得豆)
-
14. 如图,矩形ABCD中,∠BAC=60°,点E在AB上,且BE:AB=1:3,点F在BC边上运动,以线段EF为斜边在点B的异侧作等腰直角三角形GEF,连接CG,当CG最小时,的值为( )
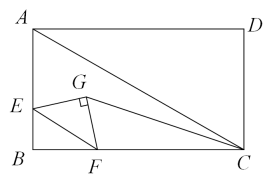 A、 B、 C、 D、15. 如图,四边形ABCD为正方形,P是以边AD为直径的⊙O上一动点,连接BP,以BP为边作等边三角形BPQ,连接OQ,若AB=2,则线段OQ的最大值为 .
A、 B、 C、 D、15. 如图,四边形ABCD为正方形,P是以边AD为直径的⊙O上一动点,连接BP,以BP为边作等边三角形BPQ,连接OQ,若AB=2,则线段OQ的最大值为 .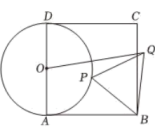 16. 如图,点O在线段AB上,OA=2,OB=6,以O为圆心,OA为半径作⊙O,点M在⊙O上运动,连结MB,以MB为一边作等边△MBC,连结AC,则AC长度的最小值为( )
16. 如图,点O在线段AB上,OA=2,OB=6,以O为圆心,OA为半径作⊙O,点M在⊙O上运动,连结MB,以MB为一边作等边△MBC,连结AC,则AC长度的最小值为( )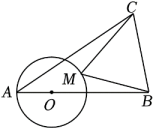 A、22 B、22 C、42 D、4217. 如图,在直角坐标系中,已知点、点 , 的半径为5,点C是上的动点,点P是线段的中点,那么长的取值范围是 .
A、22 B、22 C、42 D、4217. 如图,在直角坐标系中,已知点、点 , 的半径为5,点C是上的动点,点P是线段的中点,那么长的取值范围是 .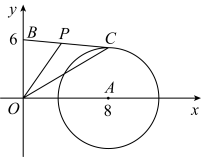 18. 在四边形中, , ;
18. 在四边形中, , ; (1)、如图1,已知 , 直接写出的度数;(2)、如图2,已知 , , , 连接 , 求的长度;(3)、如图3,已知 , , 请判断四边形的面积是否有最小值?如果有,请求出它的最小值;如果没有,请说明理由.19. 如图,抛物线y=x2-4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连接OQ,则线段OQ的最大值是( )
(1)、如图1,已知 , 直接写出的度数;(2)、如图2,已知 , , , 连接 , 求的长度;(3)、如图3,已知 , , 请判断四边形的面积是否有最小值?如果有,请求出它的最小值;如果没有,请说明理由.19. 如图,抛物线y=x2-4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段PA的中点,连接OQ,则线段OQ的最大值是( )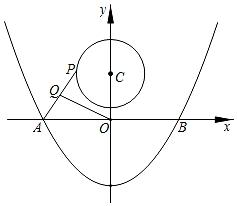 A、3 B、 C、 D、420. 如图,A是⊙B上任意一点,点C在⊙B外,已知AB=2,BC=4,△ACD是等边三角形,则 的面积的最大值为( )
A、3 B、 C、 D、420. 如图,A是⊙B上任意一点,点C在⊙B外,已知AB=2,BC=4,△ACD是等边三角形,则 的面积的最大值为( )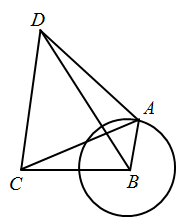 A、4 +4 B、4 C、4 +8 D、6
A、4 +4 B、4 C、4 +8 D、6三、阿氏圆(相似构造)