浙江省杭州市西湖区2023-2024学年八年级（上）数学期末试卷（提优卷）

试卷更新日期：2024-01-04 类型：期末考试

进入出卷网下载

一、选择题（共10小题，满分30分，每小题3分）

1. 下列图标是节水、节能、低碳和绿色食品的标志，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在平面直角坐标系中，点 $(m ， n)$ 位于第三象限，则（）

A、 $m < n$ B、 $m > n$ C、 $m n > 0$ D、 $m + n > 0$

查看试题解析
3. 要说明命题“若 $a^{2} > b^{2}$ ，则 $a > b$ ”是假命题，能举的一个反例是（）

A、 $a = 1$ ， $b = - 2$ B、 $a = 2$ ， $b = 1$ C、 $a = 4$ ， $b = - 1$ D、 $a = - 3$ ， $b = - 2$

查看试题解析
4. 如图，若△ABC≌△DEF，B、E、C、F在同一直线上，BC＝7，EC＝4，则CF的长是（　　）

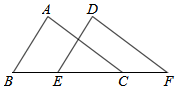A、2 B、3 C、5 D、7

查看试题解析
5. 已知a＞b ，则在下列结论中，错误的是（）

A、a+2＞b+2 B、﹣a＜﹣b C、a﹣3＞b﹣3 D、1﹣2a＞1﹣2b

查看试题解析
6. 已知点 $M (3 ， - 2)$ 与点 $N (a ， b)$ 在同一条平行于x轴的直线上，且N到y轴的距离等于4，则点N的坐标是（）

A、 $(4 ， 2)$ 或 $(- 4 ， 2)$ B、 $(4 ， - 2)$ 或 $(- 1 ， - 2)$ C、 $(4 ， - 2)$ 或 $(- 5 ， - 2)$ D、 $(4 ， - 2)$ 或 $(- 4 ， - 2)$

查看试题解析
7. 已知关于x的不等式组 ${\begin{array}{l} x + 1 \geq 2 \\ x - m < 0 \end{array}$ 有整数解，则 $m$ 的取值范围是（）

A、 $m \geq 2$ B、 $m \leq 2$ C、 $m > 1$ D、 $m \geq 1$

查看试题解析
8. 如图，在四边形 $A B C D ， D A ⊥ A B ， D A = 6 c m ， ∠ B + ∠ C = 150 ° ， A$ 刚好是 $E B$ 中点，P、Q分别是线段 $C E 、 B E$ 上的动点，则 $B P + P Q$ 的最小值为（）

A、12 B、15 C、16 D、18

查看试题解析
9. 图1是一块矩形材料 $A B C D$ ，被分割成三块， $∠ A E B = 30 °$ ， $G F ⊥ A D$ ，将三块材料无缝隙不重叠地拼成图2的形状，此时图2恰好是轴对称图形，则 $\frac{A B}{B C} = ($ $)$

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{3 - \sqrt{3}}{2}$ D、 $2 \sqrt{3} - 3$

查看试题解析
10. 已知一次函数 $y = k x + b (k \neq 0)$ 的图象与 $y = - 2 x$ 的图象交于点 $(m ， - 4)$ ．则对于不等式 $\underset{˙}{k} \underset{˙}{x} \underset{˙}{-} \underset{˙}{b} < - 2 x$ ，下列说法正确的是（）

A、当 $k < - 2$ 时， $x > 2$ B、当 $k < - 2$ 时， $x < 2$ C、当 $k > - 2$ 且 $k \neq 0$ 时， $x > - 2$ D、当 $k > - 2$ 且 $k \neq 0$ 时， $x < - 2$

查看试题解析

二、填空题(每小题4分，共24分)

11. 已知三角形三条边分别为a＋4，a＋5，a＋6，则a的取值范围是．

查看试题解析
12. 已知：如图，△ABC和△BAD中，∠C=∠D=90°，再添加一个条件就可以判断△ABC≌△BAD.

查看试题解析
13. 将点P(-1，2)向左平移2个单位，再向上平移1个单位所得的对应点的坐标为。

查看试题解析
14. 若实数m使关于x的不等式组 ${\begin{cases} 3 - \frac{2 + x}{3} \leq \frac{x + 3}{2} \\ \frac{2 x - m}{2} \leq - 1 \end{cases}$ 有解且至多有2个整数解，且使关于y的方程 $2 y = \frac{4 y - m}{3} + 2$ 的解为非负数，则满足条件的所有整数m的和为．

查看试题解析
15. 如图，一次函数y₁＝kx+b与y₂＝mx+n的图象相交于点（1，3），则方程组 ${\begin{cases} y_{1} = k x + b \\ y_{2} = m x + n \end{cases}$ 的解为 ${\begin{cases} x = 1 \\ y = 3 \end{cases}$ ，关于x的不等式kx+b＞mx+n的解为．

查看试题解析
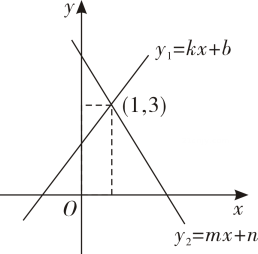16. 直线CD经过∠BCA的顶点C ， CA＝CB ． E、F分别是直线CD上两点，且∠BEC＝∠CFA＝∠α．若直线CD经过∠BCA的内部，且E、F在射线CD上，请解决下面两个问题：
①如图1，若∠BCA＝90°，∠α＝90°，则EF|BE﹣AF|（填“＞”，“＜”或“＝”号）；
②如图2，若0°＜∠BCA＜180°，若使①中的结论仍然成立，则∠α与∠BCA应满足的关系是．

查看试题解析

三、解答题（7小题，共66分）

17.

(1)、计算：2³+|﹣3|÷3﹣ $\sqrt{25}$ ×5^﹣1；

(2)、解不等式组 ${\begin{cases} 2 x > - 6 \\ \frac{x - 1}{2} \leq \frac{x + 1}{6} \end{cases}$ 并把它的解集在数轴（如图）上表示出来．

查看试题解析
18. 如图，△ABC与△DCE中，CA＝CD ， ∠1＝∠2，BC＝EC ．求证：∠A＝∠D ．

查看试题解析
19. 如图，在平面直角坐标系中（O为坐标原点），已知直线y＝kx+b与x轴y轴分别交于点A（﹣2，0）、点B（0，﹣1），点C的坐标是（0，2）．

(1)、求直线AB的表达式．

(2)、设点D为直线AB上一点，且CD＝BD ．求点D的坐标．

查看试题解析
20. 某公司研制了新产品1520kg ，为寻求合适的销售价格，进行了8天试销，共销售470kg ．统计发现每天的销售量y（千克）与销售价格x（元/千克）之间满足函数关系y＝﹣x+120．

(1)、在试销8天后，公司决定将这种产品的销售价格定为50元/千克，并且每天都按这个价格销售，则余下的产品再用多少天全部售完？

(2)、在（1）的条件下，公司继续销售9天后，发现剩余的产品必须在5天内全部售完，此时需要重新确定一个销售价格，使后面都按新的价格销售，那么新确定的价格最高不超过每千克多少元才能完成销售任务？

查看试题解析
21. 在Rt△ABC中，∠ACB＝90°，AC＝BC ， ∠CAB＝∠CBA＝45°，D为BC上一点，连接AD ，过点C作CE⊥AD于点E ．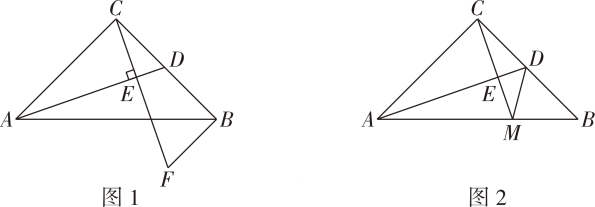

(1)、如图1，过点B作BF⊥BC交CE的延长线于点F ，求证：△ACD≌△CBF；

(2)、如图2，若D为BC的中点，CE的延长线交AB于点M ，连接DM ，求证：∠BDM＝∠ADC；

(3)、在（2）的条件下，若AE＝4，CE＝2，直接写出CM的长．

查看试题解析
22. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 是 $B C$ 边上的中点，连结 $A D$ ， $B E$ 平分 $∠ A B C$ 交 $A C$ 于点 $E$ ，过点 $E$ 作 $E F ∥ B C$ 交 $A B$ 于点 $F$ ．

(1)、若 $∠ C = 3 8^{∘}$ ，求 $∠ B A D$ 的度数；

(2)、求证： $F B = F E$ ．

查看试题解析
23.

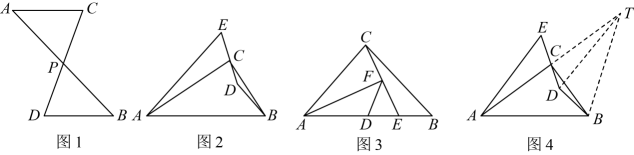(1)、【思维启迪】
如图1，点P是线段 $A B$ ， $C D$ 的中点，则 $A C$ 与 $B D$ 的数量关系为，位置关系为；

(2)、【思维探索】
如图2，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点D为 $△ A B C$ 内一点，连接 $B D$ ， $D C$ ，延长 $D C$ 到点E ，使 $C E = C D$ ，连接 $A E$ ，若 $B D ⊥ A E$ ，请用等式表示 $A B$ ， $B D$ ， $A E$ 之间的数量关系，并说明理由；
★小明思考良久后，根据 $C E = C D$ 这一条件，给出了如图4的辅助线：延长 $A C$ 到T ，使得 $C T = A C$ ，连接 $D T$ ， $B T$ ，请你根据小明给出的辅助线，继续猜想 $A B$ ， $B D$ ， $A E$ 之间的数量关系，并说明理由．

(3)、如图3，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，点D为 $A B$ 中点，点E在线段 $B D$ 上（点E不与点B ，点D重合），连接 $C E$ ，过点A作 $A F ⊥ C E$ ，连接 $F D$ ，若 $A F = 8$ ， $C F = 3$ ，请求出 $F D$ 的长．

查看试题解析