浙江省金华市金华四中2023-2024学年九年级第一学期数学12月月考试题

试卷更新日期：2024-01-04 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. 2023的相反数是（）

A、 $\frac{1}{2023}$ B、2023 C、 $- \frac{1}{2023}$ D、-2023

查看试题解析
2. 根据全国第七次人口普查结果表明，2023年金华市常住人口总数约为 $5337000$ ，数字 $5337000$ 用科学记数法表示是（）

A、 $5.337 \times 1 0^{7}$ B、 $5.337 \times 1 0^{6}$ C、 $0.5337 \times 1 0^{8}$ D、 $53.37 \times 1 0^{5}$

查看试题解析
3. 下列计算正确的是（）

A、 $(a^{2} - a b) \div a = a - a b$ B、 $3 a^{2} \cdot a = 3 a^{3}$ C、 $(a - b)^{2} = a^{2} - b^{2}$ D、 ${(a^{2})}^{3} = a^{5}$

查看试题解析
4. 有一块正方体木块，它的六个面上分别标上数字1~6，下图是这个正方体木块从不同面所看到的数字情况，请问1对面的数字是（）

A、3 B、4 C、6 D、2

查看试题解析
5. 已知正多边形的一个外角等于45°，那么这个正多边形的边数为（）

A、6 B、7 C、8 D、9

查看试题解析
6. 某居委会组织两个检查组，分别对“垃圾分类”和“违规停车”的情况进行抽查．各组随机抽取三个小区中的一个进行检查，则两个组恰好抽到同一个小区的概率是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
7. 已知二次方程 $x^{2} + b x + c = 0$ 的两根为 $- 1$ 和5，则一次函数图象 $y = b x + c$ 不经过第（）象限

A、一 B、二 C、三 D、四

查看试题解析
8. 如图，AB是圆锥的母线，BC为底面直径，已知BC=6cm，圆锥的侧面积为 $15 π$ ，则 $c o s ∠ A B O$ 的值为（）

A、 $\frac{3}{4}$ B、 $\frac{3}{5}$ C、 $\frac{4}{5}$ D、 $\frac{5}{3}$

查看试题解析
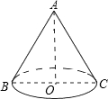9. 已知点P₁（x₁ ， y₁），P₂（x₂ ， y₂）为抛物线y＝ax²﹣4ax+c（a≠0）上两点，且x₁＜x₂ ，则下列说法正确的是（）

A、若x₁+x₂＜4，则y₁＜y₂ B、若x₁+x₂＞4，则y₁＜y₂ C、若a（x₁+x₂﹣4）＞0，则y₁＞y₂ D、若a（x₁+x₂﹣4）＜0，则y₁＞y₂

查看试题解析
10. 勾股定理的证明方法丰富多样，其中我国古代数学家赵爽利用“弦图”的证明简明、直观，是世界公认最巧妙的方法．“赵爽弦图”已成为我国古代数学成就的一个重要标志，千百年来倍受人们的喜爱．小亮在如图所示的“赵爽弦图”中，连接 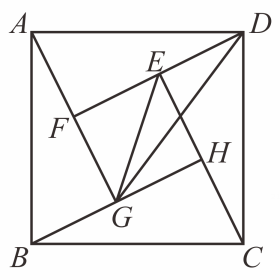$E G$ ， $D G$ ．若正方形 $A B C D$ 与 $E F G H$ 的边长之比为 $\sqrt{5} ： 1$ ，则 $s i n ∠ D G E$ 等于（）

A、 $\frac{\sqrt{10}}{10}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{3}{10} \sqrt{10}$ D、 $\frac{2}{5} \sqrt{5}$

查看试题解析

二、填空题（本大题共6小题，每小题4分，共24分）

11. 分解因式：x²－4x+4＝．

查看试题解析
12. 已知a是方程 $x^{2} - 2 x - 1 = 0$ 的解，则代数式 $a^{2} - 2 a + 2022$ 的值为．

查看试题解析
13. 某班35名同学一周课外阅读时间统计如表所示

时间/小时

7

8

9

10

人数

4

12

13

6

则该班35名同学一周课外阅读时间的众数是小时．

查看试题解析
14. 若不等式组 ${\begin{array}{l} x - a > 0 \\ 1 - x > x - 1 \end{array}$ 无解，则a的取值范围是．

查看试题解析
15. 如图，在平面直角坐标系中，△OAB的边OB在x轴的正半轴上，AO=AB ， M是边AB的中点，经过点M的反比例函数 $y = \frac{k}{x}$ （k＞0，x＞0）的图象与边OA交于点C ，则 $\frac{O C}{O A}$ 的值为．

查看试题解析
16. 如图1是超市的手推车，如图2是其侧面示意图，已知前后车轮半径均为8cm，两个车轮的圆心的连线EF与地面平行，BC与地面平行，AB $⊥$ BC ，车轮圆心F在AB的延长线上，支架FG// AD.支架CE $⊥$ CD ，测得AD=2FG ， BG=48cm，AB=42cm，CD=78cm，并测得扶手前端D到地面的距离为95cm．则点B与点F的距离为cm；手推车内装有简易宝宝椅，KZ为小坐板，打开后，椅子的支点H到点C的距离为18cm，DL=35cm，KL//BC ， HK// DE ，则坐板KL的宽度为cm.

查看试题解析

三、解答题（本大题共8小题，共66分）

17. 计算： ${(\frac{1}{2})}^{- 1} + 4 c o s 30 ° - {(5 - π)}^{0} - \sqrt{12}$ ．

查看试题解析
18. 解方程： $\frac{x}{x - 2} = \frac{1}{2 - x} - 1$ ．

查看试题解析
19. 如图，正方形网格中有一段弧，弧上三点A ， B ， C均在格点上．

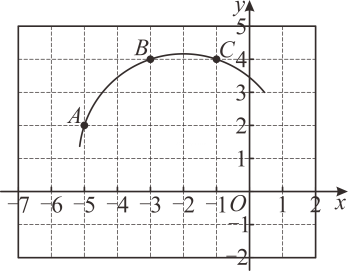(1)、请作图找出圆心P的位置，并写出它的坐标．

(2)、求 $\overset{⏜}{A C}$ 的长度．

查看试题解析
20. 4月23日是世界读书日．为了解学生的阅读喜好，丰富学校图书资源，某校将课外书籍设置了四类：文学类、科技类、艺术类、其他类，随机抽查了部分学生，要求每名学生从中选择自己最喜欢的类，将抽查结果绘制成如下统计图（不完整）．
被抽查学生最喜欢的书籍种类的
条形统计图
被抽查学生最喜欢的书籍种类的
扇形统计图
请根据图中信息解答下列问题：

(1)、求被抽查的学生人数，并求出扇形统计图中m的值．

(2)、请将条形统计图补充完整．（温馨提示：请画在答题卷相对应的图上）

(3)、若该校共有1200名学生，根据抽查结果，估计全校最喜欢“文学类”书籍的学生人数．

查看试题解析
21. 如图，数学兴趣小组的几位同学在山坡坡脚C处测得一座建筑物顶点A的仰角为60°，沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°．测得BC=60cm，AP与BC的延长线交于点D ，同学们用测倾器测得山坡的坡度为 $\frac{1}{2}$ （即 $t a n ∠ P C D = \frac{1}{2}$ ）．

(1)、求该建筑物的高度 $A B$ 的长．

(2)、求山坡上点 $P$ 处的铅直高度（测倾器的高度忽略不计，结果保留根号的形式）．

查看试题解析
22. 甲开车从A地前往B地送货，同时，乙从C地出发骑车前往B地，C在A ， B两地之间且距离A地15千米．甲到达B地后以相同的速度立马返回A地，在A地休息半小时后，又以相同的速度前往B地送第二批货，乙出发后4小时遇上送货的甲，乙让甲捎上自己（上下车时间忽略不计），甲载上乙后以原速前进．甲、乙两人距离B地的路程y（千米）与时间x（小时）之间的函数关系如图所示．

(1)、求甲第一次送货前往B地时，甲距离B地的路程y关于x的函数表达式．

(2)、问在乙距离B地多远时，甲载上了乙？

(3)、问乙比原计划早到多少时间？

查看试题解析

23. 根据以下素材，探究完成任务


素材1	图1是一个瓷碗，图2是其截面图，碗体DEC呈抛物线状(碗体厚度不计)，碗高GF=7cm，碗底宽AB=3cm，当瓷碗中装满面汤时，液面宽CD= 12cm，此时面汤最大深度EG= 6cm，
素材2	如图3，把瓷碗绕点B缓缓倾斜倒出部分面汤，当点A离MN距离为1.8cm时停止.
问题解决
任务1	确定碗体形状	在图2中建立合适的直角坐标系，求抛物线的函数表达式。
任务2	拟定设计方案1	根据图2位置，把碗中面汤喝掉一部分，当碗中液面高度(离桌面MN距离)为5cm时，求此时碗中液面宽度。
任务3	拟定设计方案2	如图3，当碗停止倾斜时，求此时碗中液面宽度CH。

查看试题解析

24. 如图1，以 $A B$ 为直径的 $⊙ O$ 与 $A H$ 相切于点A ，点C在 $A B$ 左侧圆弧上，弦 $C D ⊥ A B$ 交 $⊙ O$ 于点D ，连接 $A C ， A D$ ．点A关于 $C D$ 的对称点为E ，直线 $C E$ 交 $⊙ O$ 于点F ，交 $A H$ 于点G ．

(1)、求证： $G C = C E$ ；

(2)、当点E在 $A B$ 上，连接 $A F$ 交 $C D$ 于点P ，若 $\frac{E F}{C E} = \frac{2}{5}$ ，求 $\frac{D P}{C P}$ 的值；

(3)、当点E在射线 $A B$ 上， $A B = 2$ ，以点A ， C ， O ， F为顶点的四边形中有一组对边平行时，求 $A E$ 的长．

查看试题解析

时间/小时	7	8	9	10
人数	4	12	13	6