浙江省舟山市定海二中教育集团2023-2024学年九年级上学期数学12月月考试卷

试卷更新日期：2024-01-04 类型：月考试卷

进入出卷网下载

一、选择题(本题有10小题，每小题3分，共30分.请选出各题中唯一的正确选项，不选、多选、错选，均不给分)

1. 已知2a=3b，则下列比例式不正确的是（）

A、 $\frac{3}{a}$ = $\frac{2}{b}$ B、 $\frac{a}{3}$ = $\frac{b}{2}$ C、 $\frac{b}{a}$ = $\frac{2}{3}$ D、 $\frac{2}{a}$ = $\frac{3}{b}$

查看试题解析
2. 掷一枚质地均匀的硬币10次，下列说法正确的是（）

A、每2次必有一次正面朝上 B、必有5次正面朝上 C、可能有7次正面朝上 D、不可能有10次正面朝上

查看试题解析
3. 把抛物线 $y = 2 x^{2}$ 向右平移3个单位长度，再向下平移5个单位长度，得到的抛物线是（）

A、 $y = 2 {(x - 3)}^{2} + 5$ B、 $y = 2 {(x + 3)}^{2} + 5$ C、 $y = 2 {(x + 3)}^{2} - 5$ D、 $y = 2 {(x - 3)}^{2} - 5$

查看试题解析
4. 正十边形的每个内角都是（）

A、 $36 °$ B、 $72 °$ C、 $108 °$ D、 $144 °$

查看试题解析
5. 如图， $D E ∥ B C$ ，且 $E C ： B D = 2 ： 3$ ， $A D = 9$ ，则 $A E$ 的长为（）

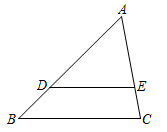A、6 B、9 C、3 D、4

查看试题解析
6. 如图，ΔABC的顶点A、B、C均在⊙O上，若 $∠ A B C + ∠ A O C = 90 °$ ，则∠AOC的大小是（）

A、30° B、45° C、60° D、70°

查看试题解析
7. 如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30°，CD=2 $\sqrt{3}$ ，则阴影部分图形的面积为（）

A、4π B、2π C、π D、 $\frac{2 π}{3}$

查看试题解析
8. 在学习画线段AB的黄金分割点时，小明先过点B作AB的垂线BC，再取AB的中点M，以点B为圆心，BM为半径画弧交射线BC于点D，连接AD，再以点D为圆心，DB为半径画弧，前后所画的两弧分别与AD交于E，F两点，最后，以A为圆心，“▗▗”的长度为半径画弧交AB于点H，点H即为AB的其中一个黄金分割点，这里的“▗▗”指的是线段（）

A、AF B、DF C、AE D、DE

查看试题解析
9. 如图，在 $R t Δ A B C$ 中， $∠ B A C = 90 °$ ，若 $A B = 6 ， A C = 8$ ，点D是AC上一点，且 $\frac{C D}{A D} = \frac{1}{3}$ ，则sin∠DBC的值为（）

A、 $\frac{\sqrt{2}}{5}$ B、 $\frac{\sqrt{2}}{10}$ C、 $\frac{\sqrt{2}}{6}$ D、 $\frac{1}{5}$

查看试题解析
10. 如图，已知二次函数 $y = - \frac{5}{4} (x + 1) (x - 4)$ 的图象与x轴交于A、B两点（点A在点B的左侧），与 $y$ 轴交于点C，P为该二次函数在第一象限内的一点，连接AP，交BC于点K，则 $\frac{A P}{P K}$ 的最小值为（）

A、 $\frac{9}{4}$ B、2 C、 $\frac{7}{4}$ D、 $\frac{5}{4}$

查看试题解析

二、填空题(本题有6小题，每小题4分，共24分)

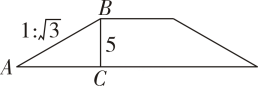
11. 如图，某地修建的一座建筑物的截面图的高 $B C = 5 m$ ，坡面AB的坡度为 $1 ： \sqrt{3}$ ，则AB的长度为。

查看试题解析
12. 一年之计在于春，为保障春播任务顺利完成，科研人员对某玉米种子在相同条件下发芽情况进行试验，结果如表：
每批粒数n
500
800
1000
2000
3000
发芽的频数m
463
768
948
1901
2851
发芽的频率 $\frac{m}{n}$
0.926
0.96
0.948
0.951
0.950
那么这种玉米发芽的概率是．（结果精确到0.01）

查看试题解析
13. 已知点A(-3，y₁)，B(-5，y₂)，C(2，y₃）在函数y=-x²-2x+b的图象上，则 $y_{1}^{} 、 y_{2}^{} 、 y_{3}^{}$ 的大小关系为（用小于符号连接）

查看试题解析
14. 如图， $A B$ 是 $⊙ O$ 的直径，弦 $C D$ 与 $A B$ 相交于点 $E$ ，若 $A E = 2$ ， $B E = 8$ ， $C E = 2 D E$ ，则 $O$ 到 $C D$ 的距离为.

查看试题解析
15. 对于一个函数，自变量 $x$ 取 $a$ 时，函数值y也等于 $a$ ，则称a是这个函数的不动点．已知二次函数 $y = x_{}^{2} + 2 x + m$ ．

(1)、若3是此函数的不动点，则m的值为．

(2)、若此函数有两个相异的不动点 $a$ ， $b$ ，且 $1 < a < b$ ，则m的取值范围为．

查看试题解析
16. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 9 0^{\circ ，} A C = 3 B C = 6 B D = 2$ ，以点B为圆心，BD长为半径作圆，点E为⊙B上的动点，连结EC，作FC⊥CE，垂足为C，点F在直线BC的上方，且满足 $C F = \frac{1}{2} C E$ ，连结BF，当点E与点D重合时，BF的值为，点E在⊙B上运动过程中，BF存在最大值为．

查看试题解析

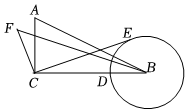
三、解答题(本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分)

17.

(1)、计算： $2 s i n 3 0^{\circ} + \sqrt{3} t a n 6 0^{\circ} - \sqrt{2} c o s 4 5^{\circ}$

(2)、已知 $\frac{a}{b} = \frac{3}{2}$ ，求 $\frac{2 a - b}{a + 2 b}$ 的值.

查看试题解析
18. 在一个不透明的口袋中装有四个大小质地相同的小球，上面分别标有数字1、2、3、4每次摸球前将袋子搅拌均匀。

(1)、若从这四个小球中随机抽取一个小球，求小球上的数字是“4”的概率；

(2)、若从这四个小球中随机抽取两个小球，用画树状图或列表的方法求取出的两个小球上的数字之积为奇数的概率是多少？

查看试题解析
19. 图1、图2均是8×8的正方形网格，每个小正方形的顶点称为格点，线段AB，CD，MN的端点均在格点上，BC与AD相交于点E，回答下列问题：

(1)、在图1中， $t a n ∠ D A B =$ ， $\frac{Δ A B E 的周长}{Δ C D E 的周长} =$ .

(2)、在图2中请用一把无刻度的尺子，画出线段MN三等分点P，Q．（保留作图痕迹）

查看试题解析
20. 如图，某建筑物BC上有一旗杆AB，小明在F处，由E观察到旗杆顶部A的仰角为52°，底部B的仰角为45°，小明的观测点与地面距离EF为1.6m，

(1)、若F与BC相距12m，求建筑物BC的高度；

(2)、若旗杆AB长3.15m，求建筑物BC的高度．（结果精确到0.1m）（参考数据： $\sqrt{2} \approx 1.414 ， s i n 5 2^{\circ} \approx 0.788$ .788，tan52°≈1.280).

查看试题解析
21. 如图，四边形ABCD内接于⊙O，分别延长BC，AD，使它们相交于点E， $A B = 8$ ，且 $D C = D E$

(1)、求证： $∠ A = ∠ A E B .$

(2)、若 $∠ E D C = 9 0^{\circ}$ ，点C为BE的中点，求⊙O的半径．

查看试题解析
22. 为了充分利用四边形余料，小明设计了不同的方案裁剪正方形，裁剪方案与数据如表：
方案设计
方案1
方案2
裁剪方案示意图
说明
图中的正方形AEFG和正方形MNPO四个顶点都在原四边形的边上
测量数据
AD=9dm，CD=2dm，AB=14dm，∠A=∠D=90°；

(1)、任务1：探寻边角填空：BC=dm；sinB=；

(2)、任务2：比较面积计算或推理：正方形AEFG和正方形MNP边长之比；

(3)、任务3：应用实践若在△BEF余料上再截取一个最大正方形，正方形的边长为dm.

查看试题解析
23. 在二次函数 $y = x_{}^{2} - 2 t x + 3 (t > 0)$ 中：

(1)、若它的图象过点（2，1），则t的值为多少？

(2)、当 $0 \leq x \leq 3$ 时，y的最小值为-2，求出t的值：

(3)、如果A $(m - 2 ， a)$ ， B $(4 ， b)$ ， C $(m ， a)$ 都在这个二次函数的图象上，且 $a < b < 3$ 求m的取值范围。

查看试题解析
24. 如图，AD是ΔABC的外角∠EAC的平分线，与ΔABC的外接圆⊙O交于点D，连结BD交AC于点F.

(1)、求证： $B D = C D .$

(2)、若 $∠ B A C = 6 0^{\circ} ，$ BC＝3．当AF将ΔABD的面积分为1：2两部分时，求ΔADF与ΔBCF的面积比值.

(3)、将C点关于AD的对称点记为点C＇，当 $B C^{'} = \sqrt{3}$ BD时，写出AD与半径r的数量关系，并说明理由.

查看试题解析

每批粒数n	500	800	1000	2000	3000
发芽的频数m	463	768	948	1901	2851
发芽的频率 $\frac{m}{n}$	0.926	0.96	0.948	0.951	0.950

方案设计	方案1	方案2
裁剪方案示意图
说明	图中的正方形AEFG和正方形MNPO四个顶点都在原四边形的边上
测量数据	AD=9dm，CD=2dm，AB=14dm，∠A=∠D=90°；

浙江省舟山市定海二中教育集团2023-2024学年九年级上学期数学12月月考试卷

一、选择题(本题有10小题，每小题3分，共30分.请选出各题中唯一的正确选项，不选、多选、错选，均不给分)

二、填空题(本题有6小题，每小题4分，共24分)

三、 解答题(本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分)

三、解答题(本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分)