浙江省湖州市安吉县2023-2024学年九年级上册数学12月月考试卷
试卷更新日期:2024-01-04 类型:月考试卷
一、选择题(本大题共10小题,共30分)
-
1. 如果 , 那么( )A、 B、 C、 D、2. 袋子中装有2个白球,5个红球,3个黄球,任意摸出一个球,是红球的概率是( )A、 B、 C、 D、3. 如图,在的内接四边形中,点在的延长线上.若 , 则的度数是( )
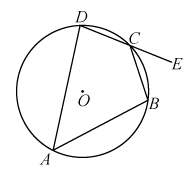 A、 B、 C、 D、4. 如图,在中, , , 若 , 则等于( )
A、 B、 C、 D、4. 如图,在中, , , 若 , 则等于( )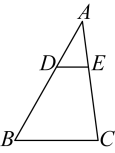 A、6 B、8 C、7 D、55. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度后,得到抛物线的解析式为( )A、 B、 C、 D、6. 如图所示,四边形中, , , , , , 若与相似,则符合条件的点个数是( )
A、6 B、8 C、7 D、55. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度后,得到抛物线的解析式为( )A、 B、 C、 D、6. 如图所示,四边形中, , , , , , 若与相似,则符合条件的点个数是( )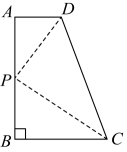 A、0 B、1 C、2 D、37. 已知抛物线经过点 , 则该抛物线必然还经过点( )A、 B、 C、 D、8. 如图,是的直径,点C、D、E在上,若 , , 且 , 则为( )
A、0 B、1 C、2 D、37. 已知抛物线经过点 , 则该抛物线必然还经过点( )A、 B、 C、 D、8. 如图,是的直径,点C、D、E在上,若 , , 且 , 则为( )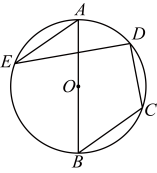 A、 B、6 C、 D、9. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )
A、 B、6 C、 D、9. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )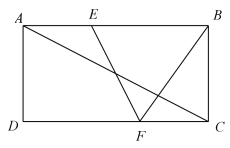 A、 B、 C、4 D、610. 如图,在四边形 中,以 为直径的 恰好经过点 , , 交于点 ,已知 平分 , , ,则 的值为( )
A、 B、 C、4 D、610. 如图,在四边形 中,以 为直径的 恰好经过点 , , 交于点 ,已知 平分 , , ,则 的值为( )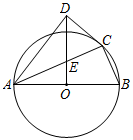 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共24分)
-
11. 将二次函数用配方法化成的形式为y= .12. 在一个不透明的布袋中,黄色、红色的乒乓球共10个,这些球除颜色外其他都相同.小刚通过多次摸球实验后发现其中摸到黄球的频率稳定在60%,则布袋中红色球的个数很可能是个.13. 扇形的圆心角为80°,弧长为4πcm,则此扇形的面积等于cm2 .14. 如图,我国古代建造的闻名中外的赵州石拱桥,若桥拱圆弧的半径长为 , 拱高为 , 则桥跨度为(用含r、h的代数式表示)
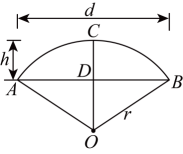 15. 有五本形状为长方体的书放置在方形书架中,如图所示,其中四本竖放,第五本斜放,点 正好在书架边框上.每本书的厚度为5cm,高度为20cm,书架宽为40cm,则 的长.
15. 有五本形状为长方体的书放置在方形书架中,如图所示,其中四本竖放,第五本斜放,点 正好在书架边框上.每本书的厚度为5cm,高度为20cm,书架宽为40cm,则 的长.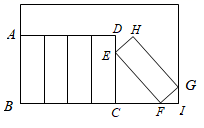 16. 抛物线与轴相交于不同两点、 , 若存在整数及整数 , 使得和同时成立,则 .
16. 抛物线与轴相交于不同两点、 , 若存在整数及整数 , 使得和同时成立,则 .三、解答题(本大题共8小题,共66分。解答应写出文字说明,证明过程或演算步骤)
-
17.(1)、已知线段 , 求线段a , b的比例中项线段c的长.(2)、已知 , 求的值.18. 已知二次函数图象的顶点坐标是 , 且经过点 .(1)、求这个二次函数的表达式;(2)、若点在该函数图象上,求点的坐标.19. 为了更好的感受中考考法,精准备考,学生和学生两位同学,分别从2020、2021、2022、2023四年的浙江中考真题中选择一套完成,四套题分别记为A、B、C、D , 若他们两人选择哪一套题相互不受影响,且选择每一套题的几率均等.(1)、他们都选择“2023”的概率为;(2)、请用列表或画树状图的方法,求两人都不选择“2023”的概率20. 如图,在中, , 以腰为直径画半圆 , 分别交 , 于点D , E .
 (1)、求证:;(2)、若 , , 求阴影部分弓形的面积.21. 毛泽东故居景区有一商店销售一种纪念品,这种商品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种商品的销售价不高于20元/件,市场调查发现,该商品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)、求证:;(2)、若 , , 求阴影部分弓形的面积.21. 毛泽东故居景区有一商店销售一种纪念品,这种商品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种商品的销售价不高于20元/件,市场调查发现,该商品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.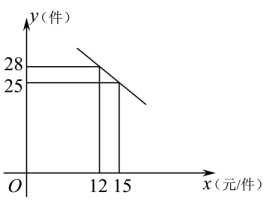 (1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?22. 如图,内接于 , , 它的外角的平分线交于点D , 连接交于点F .
(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?22. 如图,内接于 , , 它的外角的平分线交于点D , 连接交于点F . (1)、若 , 求的度数.(2)、求证: .(3)、若 , 当 , 求的度数(用含的代数式表示).23. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 抛物线经过 , 两点,与轴的另一个交点为点 .
(1)、若 , 求的度数.(2)、求证: .(3)、若 , 当 , 求的度数(用含的代数式表示).23. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 抛物线经过 , 两点,与轴的另一个交点为点 .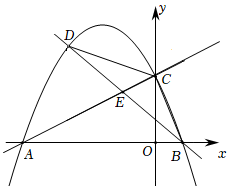 (1)、求抛物线的函数表达式.(2)、点为直线上方抛物线上一动点,连接 , , 设直线交线段于点 , 的面积为 , 的面积为 , 求的最大值.24. 如图1,在△ABC中,AB=AC=2,∠BAC=120°,点D、E分别是AC、BC的中点,连接DE .
(1)、求抛物线的函数表达式.(2)、点为直线上方抛物线上一动点,连接 , , 设直线交线段于点 , 的面积为 , 的面积为 , 求的最大值.24. 如图1,在△ABC中,AB=AC=2,∠BAC=120°,点D、E分别是AC、BC的中点,连接DE . (1)、探索发现:
(1)、探索发现:图1中,的值为 , 的值为 .
(2)、拓展探究若将△CDE绕点C旋转,在旋转过程中的大小有无变化?请仅就图2的情形给出证明.
(3)、问题解决当△CDE旋转至A , D , C三点共线时,直接写出线段BE的长.