四川省绵阳市南山名校2023-2024学年高三上学期12月月考数学(理)试题
试卷更新日期:2024-01-04 类型:月考试卷
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 复数 的共轭复数是( )A、 B、 C、 D、2. 已知集合 , , 则( )A、 , B、 , C、 , D、 ,3. 若是夹角为的两个单位向量,与垂直,则( )A、 B、 C、 D、4. 若 , 满足约束条件 , 则的最大值为( )A、25 B、27 C、29 D、305. 函数的大致图象为( )A、
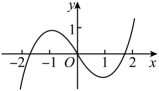 B、
B、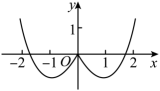 C、
C、 D、
D、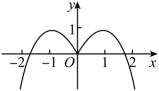 6. 已知点是抛物线的焦点,点 , 且点为抛物线上任意一点,则的最小值为( )A、7 B、6 C、5 D、47. 已知的展开式中常数项为24,则的值为( )A、1 B、 C、2 D、8. 七辆汽车排成一纵队,要求甲车、乙车、丙车均不排队头或队尾且各不相邻,则排法有( )A、48种 B、72种 C、90种 D、144种9. 已知函数 , 将的图象向右平移个单位长度后,得到的图象.若的图象关于直线对称,则( )A、 B、 C、 D、10. 已知圆 , 是圆上的一条动弦,且 , 为坐标原点,则的最小值为( )A、 B、 C、 D、11. 双曲线C:( , )的一条渐近线过点 , , 是C的左右焦点,且 , 若双曲线上一点M满足 , 则( )A、或 B、 C、 D、12. 若实数a,b, , 且满足 , , , 则a,b,c的大小关系是( )A、c>b>a B、b>a>c C、a>b>c D、b>c>a
6. 已知点是抛物线的焦点,点 , 且点为抛物线上任意一点,则的最小值为( )A、7 B、6 C、5 D、47. 已知的展开式中常数项为24,则的值为( )A、1 B、 C、2 D、8. 七辆汽车排成一纵队,要求甲车、乙车、丙车均不排队头或队尾且各不相邻,则排法有( )A、48种 B、72种 C、90种 D、144种9. 已知函数 , 将的图象向右平移个单位长度后,得到的图象.若的图象关于直线对称,则( )A、 B、 C、 D、10. 已知圆 , 是圆上的一条动弦,且 , 为坐标原点,则的最小值为( )A、 B、 C、 D、11. 双曲线C:( , )的一条渐近线过点 , , 是C的左右焦点,且 , 若双曲线上一点M满足 , 则( )A、或 B、 C、 D、12. 若实数a,b, , 且满足 , , , 则a,b,c的大小关系是( )A、c>b>a B、b>a>c C、a>b>c D、b>c>a二、填空题:本大题共4小题,每小题5分,共20分.
-
13. 函数的图象在处的切线方程为14. 已知是各项均不相同的等差数列,是公比为q的等比数列,且 , 则 .15. 已知椭圆的右焦点与抛物线的焦点重合,且与该抛物线在第一象限交于点 , 若轴,则椭圆C的离心率为 .16. 人脸识别,是基于人的脸部特征信息进行身份识别的一种生物识别技术.在人脸识别中,主要应用距离测试检测样本之间的相似度,常用测量距离的方式有曼哈顿距离和余弦距离.设 , 则曼哈顿距离 , 余弦距离 , 其中(O为坐标原点).已知点 , 则的最大值近似等于.(保留3位小数)(参考数据:.)
三、解答题(一):必考题:60分。解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题.
-
17. 已知单调递增数列的前项和为 , 且 .(1)、求的通项公式;(2)、记 , 求数列的前项和 .18. 在中,角A,B,C的对边分别为a,b,c, , .(1)、求角B;(2)、若 , , D为AC边的中点,求的面积.19. 2023年上海书展于8月16日至22日在上海展览中心举办.展会上随机抽取了50名观众,调查他们每个月用在阅读上的时长,得到如图所示的频率分布直方图:
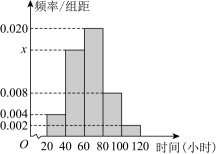 (1)、求x的值,并估计这50名观众每个月阅读时长的平均数;(2)、用分层抽样的方法从这两组观众中随机抽取6名观众,再若从这6名观众中随机抽取2人参加抽奖活动,求所抽取的2人恰好都在这组的概率.20. 设椭圆的左右顶点分别为 , 左右焦点.已知 , .(1)、求椭圆方程.(2)、若斜率为1的直线交椭圆于A,B两点,与以为直径的圆交于C,D两点.若 , 求直线的方程.21. 已知函数 .(1)、当时,求的零点个数;(2)、若恒成立,求实数a的值.
(1)、求x的值,并估计这50名观众每个月阅读时长的平均数;(2)、用分层抽样的方法从这两组观众中随机抽取6名观众,再若从这6名观众中随机抽取2人参加抽奖活动,求所抽取的2人恰好都在这组的概率.20. 设椭圆的左右顶点分别为 , 左右焦点.已知 , .(1)、求椭圆方程.(2)、若斜率为1的直线交椭圆于A,B两点,与以为直径的圆交于C,D两点.若 , 求直线的方程.21. 已知函数 .(1)、当时,求的零点个数;(2)、若恒成立,求实数a的值.四、解答题(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题记分.