吉林省四平市2023-2024学年高一上学期12月第二次月考数学试题
试卷更新日期:2024-01-04 类型:月考试卷
一、单项选择题(本题共8小题,每题5分,共计40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. “”是“”的( )A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件2. 已知函数 , 则该函数的单调递增区间为( )A、 B、 C、 D、3. 已知扇形面积为 , 半径是1,则扇形的圆心角是( )A、 B、 C、 D、4. 我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来琢磨函数的图象的特征,如函数的图象大致是( )A、
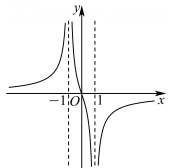 B、
B、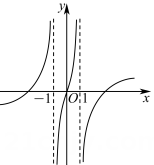 C、
C、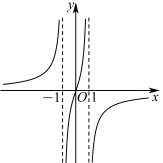 D、
D、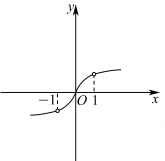 5. 已知 , 且满足 , 则的最小值是( )A、2 B、4 C、3 D、66. 若是奇函数,且函数在有最大值8,则函数在有( )A、最小值 B、最大值 C、最小值 D、最小值7. 已知函数 , 若 , 则的大小关系为( )A、 B、 C、 D、8. 已知函数 , , 的零点分别为a,b,c,下列各式正确的是( )A、 B、 C、 D、
5. 已知 , 且满足 , 则的最小值是( )A、2 B、4 C、3 D、66. 若是奇函数,且函数在有最大值8,则函数在有( )A、最小值 B、最大值 C、最小值 D、最小值7. 已知函数 , 若 , 则的大小关系为( )A、 B、 C、 D、8. 已知函数 , , 的零点分别为a,b,c,下列各式正确的是( )A、 B、 C、 D、二、多项选择题(本题共4小题,每题5分,共计20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
-
9. 下列说法正确的是( )A、所有幂函数的图象均过点 B、若幂函数的图象经过点 , 则解析式为 C、幂函数一定具有奇偶性 D、任何幂函数的图象都不经过第四象限10. 下列四个结论中,正确的是( )A、角和角的终边重合,则 B、角和角的终边关于原点对称,则 C、角和角的终边关于轴对称,则 D、角和角的终边关于轴对称,则11. 已知偶函数的定义域为 , 对任意两个不相等的正数 , 都有 , 则下列结论正确的是( )A、 B、 C、 D、12. 定义 , 若函数 , 且在区间上的值域为 , 则区间长度可以是( )A、 B、 C、 D、1
三、填空题(本题共4小题,每题5分,共计20分)
-
13. 已知函数的定义域为 , 则函数的定义域为 .14. 已知命题;命题 . 若都是假命题,则实数的取值范围是 .15. 高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设表示不超过的最大整数,则称为高斯函数,例如: , , 已知函数 , 则函数的值域为 .16. 已知函数 , 若 , 且 , 给出下列结论:① , ② , ③ , ④ , 其中所有正确命题的编号是 .
四、解答题(本题共6小题,共计70分.解答应写出文字说明、证明过程或演算步骤)
-
17.(1)、求值;(2)、已知为正实数, , 求的值.18. 已知集合 .(1)、若 , 存在集合使得 , 求这样的集合;(2)、若集合是集合的一个子集,求的取值范围.19. 定义:对于定义域为的函数 , 若 , 有 , 则称为的不动点.已知函数 .(1)、当时,求函数的不动点;(2)、设 , 若有两个不动点为 , 且 , 求实数的最小值.20. “凤眼蓝”是一种花朵为浅蓝色的浮水草本植物,它是我国园林水景中的常用造景材料,并且适宜在污染严重的水中生长,是监测环境污染的良好植物.某市2019年底为了净化某水库的水质,引入“凤眼蓝”,这些“凤眼蓝”在水中蔓延速度越来越快,2020年1月底“凤眼蓝”覆盖面积为 , 到了4月底测得“凤眼蓝”覆盖面积为 , “凤眼蓝”覆盖面积(单位:)与月份(单位:月)的关系有两个函数模型(且)与可供选择.(1)、分别求出两个函数模型的解析式;(2)、经测得2020年5月底“凤眼蓝”的覆盖面积约为 , 从上述两个函数模型中选择更合适的一个模型,并求“凤眼蓝”覆盖面积达到时的最小月份.(参考数据:)