湖北省武汉市武汉榕霖文化艺术学院2023-2024学年高一上学期12月月考数学试卷
试卷更新日期:2024-01-04 类型:月考试卷
一、单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 已知集合 , 则集合( )A、 B、 C、 D、2. 已知集合 , 若 , 则( )A、1 B、 C、2 D、-1
3. 已知函数 , 则的值是( )A、 B、 C、 D、24. 设 , 则( )A、 B、 C、 D、5. 已知函数 , 则对任意实数 , 有( )A、 B、 C、 D、6. 式子的计算结果为( )A、1 B、 C、 D、7. 函数 的图象大致为( )A、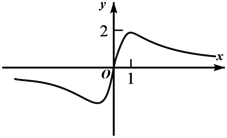 B、
B、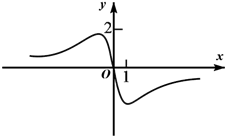 C、
C、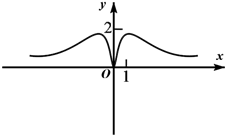 D、
D、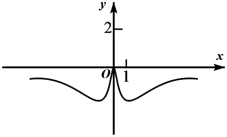 8. 已知函数 , 若任意的 , 都有成立,则的取值范围为( )A、 B、 C、 D、
8. 已知函数 , 若任意的 , 都有成立,则的取值范围为( )A、 B、 C、 D、二、多选题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项是符合题目要求的,全对得5分,部分选对得2分,选错不得分)
-
9. 下列函数中为偶函数且在上单调递增的是( )A、 B、 C、 D、10. 下列各式正确的是( )A、 B、 C、 D、11. 已知 , 则函数的图像可能是( )A、
 B、
B、 C、
C、 D、
D、 12. 设是定义在上的奇函数,且在上单调递减, , 则( )A、在上单调递减 B、 C、不等式的解集为 D、的图象与轴只有1个交点
12. 设是定义在上的奇函数,且在上单调递减, , 则( )A、在上单调递减 B、 C、不等式的解集为 D、的图象与轴只有1个交点三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
-
13. 函数的定义域是.14. 若且 , 则函数的图像恒过的定点的坐标为 .15. 从甲市到乙市的电话费由函数给出,其中为不超过的最大整数,则从甲市到乙市的电话费为元.16. 若函数是上的偶函数,且当时, , 则.
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
-
17. 求值:(1)、(2)、18. 已知函数.(1)、若 , 求实数的值;(2)、若 , 恒成立,求:实数的取值范围.19. 已知幂函数为偶函数.(1)、求的解析式;(2)、若函数在区间上的最大值为9,求实数的值.
