2023-2024学年浙教版数学七年级(上)期末仿真模拟卷(三)
试卷更新日期:2024-01-04 类型:期末考试
一、选择题
-
1. 如果表示收到5元红包,那么表示( )A、余额不足3元 B、余额有3元 C、发出3元红包 D、收到3元红包2. 若 , 为有理数, , ,且 ,那么 , , , 的大小关系是( )A、 B、 C、 D、3. 单项式的系数和次数分别是( )A、 B、 C、 D、4. 下列各组数中是同类项的是( )A、4x和4y B、和 C、和 D、和5. 设x,y,c是实数,正确的是( )A、若x=y,则x+c=y﹣c B、若x=y,则xc=yc C、若x=y,则 D、若 , 则2x=3y6. 下列解方程中,移项正确的是( )A、由5+x=18,得x=18+5 B、由5x+ =3x,得5x-3x= C、由x+3= x-4,得x+ x=-4-3 D、由3x-4=6x,得3x+6x=4.7. 已知某商店有两个进价不同商品都卖了80元,其中一个盈利60%,另一个亏损20%,在这次买卖中,这家商店( )A、盈利50元 B、亏损10元 C、盈利10元 D、不盈不亏8. 用一个平面去截一个几何体,截面不可能是圆的几何体的是( )A、
 B、
B、 C、
C、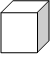 D、
D、 9. 如图,从A地到B地有四条路线,由上到下依次记为路线①、②、③、④,则从A地到B地的最短路线是路线( ).
9. 如图,从A地到B地有四条路线,由上到下依次记为路线①、②、③、④,则从A地到B地的最短路线是路线( ).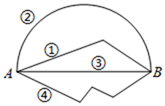 A、① B、② C、③ D、④10. 在同一平面内,点在直线上,与互补, , 分别为 , 的平分线,若 , 则( )A、 B、 C、 D、
A、① B、② C、③ D、④10. 在同一平面内,点在直线上,与互补, , 分别为 , 的平分线,若 , 则( )A、 B、 C、 D、二、填空题
-
11. 已知:|x|=3,|y|=2,且xy<0,则x+y的值为等于.12. 单项式 的系数是 .13. 方程的解为 .14. 已知∠α=60°36′,则∠α的余角是 . (用度表示)15. 用四舍五入法对3.444 5取近似数,即3.4445 (精确到百分位)≈16. 规定:对于确定位置的三个数a,b,c,计算 , 将这三个数的最小值称为a,b,c的“白马数”.例如, 对于1,-2,3 ,因为 . 所以1,-2 ,3的“白马数”为 . 调整-1,6,x这三个数的位置 ,得到不同的“白马数”, 若其中的一个“白马数”为2,则x= .
三、综合题
-
17. 如图,A,B两点在数轴上对应的数分别为a,b,且点A在点B的左边,|a|=10,a+b=80,ab<0.
 (1)、求出a,b的值;(2)、现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.
(1)、求出a,b的值;(2)、现有一只电子蚂蚁P从点A出发,以3个单位长度/秒的速度向右运动,同时另一只电子蚂蚁Q从点B出发,以2个单位长度/秒的速度向左运动.①设两只电子蚂蚁在数轴上的点C相遇,求出点C对应的数是多少?
②经过多长时间两只电子蚂蚁在数轴上相距20个单位长度?
18. 如图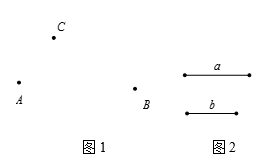 (1)、如图1,平面上有3个点A,B,C.
(1)、如图1,平面上有3个点A,B,C.①画直线AB;画射线BC;画线段AC;
②过点C作AB的垂线,垂足为点D;
③量出点C到直线AB的大约距离.
(2)、尺规作图:已知:线段a,b,如图2.
求作:一条线段MN,使它等于2a-b.(不写作法,保留作图痕迹)
19. 如图,点是直线上一点,点是线段的中点. (1)、若 , 点在线段上,且 , 则的长为.(2)、若 , , 求的长(用含的代数式表示).20. 某网店用16500元的资金购进A, B两种商品共500件,并在“双十一”期间销售,两种商品的进价和售价如下表所示:
(1)、若 , 点在线段上,且 , 则的长为.(2)、若 , , 求的长(用含的代数式表示).20. 某网店用16500元的资金购进A, B两种商品共500件,并在“双十一”期间销售,两种商品的进价和售价如下表所示:进价(元)
售价(元)
A
60
84
B
15
20
(1)、求A商品购进的数量.(2)、A商品售出 , B商品售出后,由于销售情况不理想,网店推出“买一件A商品送一件B商品,单独购买B商品优惠m元”的促销活动.一段时间后,A,B两种商品全部售完.已知剩余的A商品都参加了促销活动,销售A,B两种商品共获利3200元,求m的值.21.(1)、已知单项式的次数与多项式的次数相同,则;(2)、若多项式与多项式的差中不含x的二次项,求m的值.22. 某中学到商店购买足球和排球,购买足球40个,排球30个共花费4000元,已知购买一个足球比购买一个排球多花30元.(1)、求购买一个足球和一个排球各需多少元?(2)、学校决定第二次购买足球和排球共50个,正好赶上商场对商品价格进行调整,一个足球售价比第一次购买时提高了10%,一个排球按第一次购买时售价的九折出售,如果学校第二次购买足球和排球的总费用是第一次购买总费用的86%,求学校第二次购买排球多少个?23. 如图,已知线段 , 点为上的一个动点,点、分别是和的中点. (1)、若点恰好是中点,则;(2)、若 , 求的长;(3)、试利用“字母代替数”的方法,说明不论取何值(不超过 , 的长不变.24. 为了推进1+3素养提升行动,某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售某种同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副乒乓球拍赠一盒乒乓球,乙店全部按定价的9折优惠,该班准备选择其中一家商店购买乒乓球拍6副,乒乓球x盒(x>6).(1)、用含x的代数式表示在这两家商店购买各需付款多少元;(2)、若购买15盒乒乓球,请你通过计算,说明此时在哪家商店购买较为合算?(3)、当购买乒乓球多少盒时,到这两家商店付款一样多.
(1)、若点恰好是中点,则;(2)、若 , 求的长;(3)、试利用“字母代替数”的方法,说明不论取何值(不超过 , 的长不变.24. 为了推进1+3素养提升行动,某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售某种同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副乒乓球拍赠一盒乒乓球,乙店全部按定价的9折优惠,该班准备选择其中一家商店购买乒乓球拍6副,乒乓球x盒(x>6).(1)、用含x的代数式表示在这两家商店购买各需付款多少元;(2)、若购买15盒乒乓球,请你通过计算,说明此时在哪家商店购买较为合算?(3)、当购买乒乓球多少盒时,到这两家商店付款一样多.