北师大版数学七年级上册期末冲刺满分攻略19 一元一次方程的应用

试卷更新日期：2024-01-03 类型：复习试卷

进入出卷网下载

一、选择题

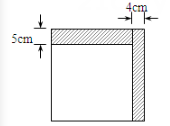
1. 如图，小明将一个正方形纸片剪去一个宽为4cm的长条后，再从剩下的长方形纸片上剪去一个宽为5cm的长条，如果两次剪下的长条面积正好相等，那么每一个长条的面积为（）

A、16 $c m^{2}$ B、20 $c m^{2}$ C、80 $c m^{2}$ D、160 $c m^{2}$

查看试题解析
2. 如图，直线AB，CD相交于点O，AOC30，OE⊥AB，OF是AOD的角平分线．若射线OE，OF分C别以18/s，3/s的速度同时绕点O顺时针转动，当射线OE，OF重合时，至少需要的时间是（）

A、8s B、11s C、 $\frac{41}{3}$ s D、13s

查看试题解析
3. 已知圆柱体的高是10厘米，沿着底面直径垂直切开，把圆柱分成相等的两半，表面积增加了40平方厘米，这个圆柱体的体积是（）立方厘米。(全卷π均取3.14)

A、62.8 B、125.6 C、31.4 D、251.2

查看试题解析
4. 把一段圆柱形钢材削成一个最大的圆锥体，切掉的部分重12千克，求原钢材重多少千克？正确的算式是（）。

A、12÷ $\frac{1}{3}$ B、12×3 C、12×2 D、12÷ $\frac{2}{3}$

查看试题解析
5. 某品牌冰箱去年国庆节开始季节性降低20%，到今年五一节又季节性涨价20%后，现售价为2400元/台，则该品牌冰箱去年国庆节之前的售价为每台（）

A、2000元 B、2500元 C、2400元 D、2200元

查看试题解析
6. 一商家进行促销活动，某商品的优惠措施是“第二件商品打6折”．现购买2件该商品，相当于这2件商品共打了（）．

A、7折 B、8折 C、7.5折 D、8.5折

查看试题解析
7. 某中学的学生自己动手整修操场，七年级的学生说：“如果让我们单独工作，7.5小时能完成”；八年级的学生说：“如果让我们单独工作，5小时能完成.”现两个年级学生一起工作1小时，剩下的部分再让七年级单独完成需x小时，可列方程（）

A、 $\frac{1}{7.5} - \frac{1}{5} - \frac{x}{7.5} = 1$ B、 $\frac{1}{7.5} - \frac{1}{5} + \frac{x}{7.5} = 1$ C、 $\frac{1}{7.5} + \frac{1}{5} - \frac{x}{7.5} = 1$ D、 $\frac{1}{7.5} + \frac{1}{5} + \frac{x}{7.5} = 1$

查看试题解析
8. 一件工程，甲单独做需12天完成，乙单独做需8天完成，现先由甲、乙合作2天后，乙有其他任务，剩下的工程由甲单独完成，则甲还需要（）天才能完成该工程

A、 $6 \frac{3}{4}$ B、 $7 \frac{1}{3}$ C、6 D、7

查看试题解析
9. 如图，电子蚂蚁 $P 、 Q$ 在边长为1个单位长度的正方形 $A B C D$ 的边上运动，电子蚂蚁 $P$ 从点 $A$ 出发，以 $\frac{3}{2}$ 个单位长度/秒的速度绕正方形作顺时针运动，电子蚂蚁 $Q$ 从点 $A$ 出发，以 $\frac{1}{2}$ 个单位长度/秒的速度绕正方形作逆时针运动，则它们第2019次相遇在（）

A、点 $A$ B、点 $B$ C、点 $C$ D、点 $D$

查看试题解析
10. 甲乙两人练习赛跑，甲每秒跑7米，乙每秒跑6.5米，甲让乙先跑5米，设x秒后，甲可以追上乙，则下列方程不正确结果是（　　）

A、7x=6.5x+5 B、7x﹣5=6.5 C、（7﹣6.5）x=5 D、6.5x=7x﹣5

查看试题解析

二、填空题

11. 已知数轴上两点A、B对应的数分别为﹣1与3．点P从A点出发，以每秒2个单位长度的速度沿数轴的正方向匀速运动；同时点Q从B点出发，以每秒1个单位长度沿数轴匀速运动．设P、Q两点的运动时间为t秒，当PQ＝ $\frac{1}{2}$ AB时，t＝．

查看试题解析
12. 某种商品的标价为200元，为了吸引顾客，按九折出售，这时仍要盈利20%，则这种商品的进价是元．

查看试题解析
13. $A$ ， $B$ 两地相距 $450$ 千米，甲、乙两车分别从 $A$ ， $B$ 两地同时出发，相向而行，已知甲速度为 $120$ 千米/时，乙速度为 $80$ 千米/时， $t$ 小时后两车相距 $50$ 千米， $t$ 满足的方程是.

查看试题解析
14. 甲､乙两人检修一条长 $1000 m$ 的煤气管道，甲每小时检修 $100 m$ ，乙每小时检修 $150 m$ 现在两人合作，需要小时完成．

查看试题解析
15. 如图，这是某超市“飘柔”洗发水的价格标签，一位服务员不小心将标签弄脏了，使得原价看不清．请你帮忙算一算，该洗发水的原价是元．

查看试题解析
16. 实验室里，水平桌面上有甲、乙、丙三个相同高度的圆柱形容器（容器足够高），底面半径之比为1：2：1，用两个相同的管子在10cm高度处连通（即管子底部离容器底10cm），现三个容器中，只有乙中有水，水位高4cm，如图所示．若每分钟同时向甲和丙注入相同量的水，开始注水1分钟，甲的水位上升3cm．则开始注入分钟水量后，甲的水位比乙高1cm．

查看试题解析

三、计算题

17. 一艘载重480吨的船，容积是1050立方米，现有甲种货物450立方米，乙种货物350吨，而甲种货物每吨体积2.5立方米，乙种货物每立方米0.5吨．问是否都能装上船？如果不能，请说明理由；并求出为了最大限度的利用船的载重量和容积，两种货物应各装多少吨？

查看试题解析
18. 一列匀速前进的火车，通过列车隧道.

(1)、如果通过一个长300米的隧道AB，从车头进入隧道到车尾离开隧道，共用15秒的时间（如图1），又知其间在隧道顶部的一盏固定的灯发出的一束光垂直照射火车2.5秒，求这列火车的长度；

图一

(2)、如果火车以相同的速度通过了另一个隧道CD，从火车车尾全部进入隧道到火车车头刚好到达隧道出口（如图2），其间共用20秒时间，求这个隧道CD的长.

图二

查看试题解析
19. 某市为保障供水及道路安全，自来水有限公司排查地下管线密集区，决定改造一段已使用多年面临老化的自来水管，这项翻新工程如果由甲工程队单独改造需要12天，由乙工程队单独改造需要24天．现要求甲、乙两个工程队一起合作完成这项翻新工程，但由于工作调动的原因，该项工程完工时，乙工程队中途共离开了3天，问这项工程一共用了多少天？

查看试题解析
20. 一套仪器由一个A部件和三个B部件构成，用1立方米钢材可做40个A部件或240个B部件．现要用6立方米钢材制作这种仪器，应用多少钢材制作A部件，才能使生产的A、B刚好配套？恰好配成这种仪器多少套？

查看试题解析
21. 小魏和小梁从A，B两地同时出发，小魏骑自行车，小梁步行，沿同条路线相向匀速而行。出发2h两人相遇。相遇时小魏比小梁多行24km，相遇后0.5h小魏到达B地.

(1)、两人的速度分别是多少?

(2)、相遇后小梁多少时间到达A地?

查看试题解析
22. 某超市第一次以4450元购进甲、乙两种商品，其中乙商品的件数是甲商品件数的2倍多15件，甲、乙两种商品的进价和售价如下表：（注：利润＝售价－进价）

甲
乙
进价（元/件）
20
30
售价（元/件）
25
40

(1)、该超市第一次购进甲、乙两种商品各多少件？

(2)、该超市第二次以第一次的进价又购进甲、乙两种商品，其中乙商品的件数不变，甲商品的件数是第一次的2倍；乙商品按原价销售，甲商品打折销售，第二次两种商品都销售完以后获得的总利润与第一次获得的总利润一样，求第二次甲商品是按原价打几折销售？

查看试题解析

23. 列方程式应用题．

天河食品公司收购了200吨新鲜柿子，保质期15天，该公司有两种加工技术，一种是加工为普通柿饼，另一种是加工为特级霜降柿饼，也可以不需加工直接销售．相关信息见表：

品种	每天可加工数量（吨）	每吨获利（元）
新鲜柿子	不需加工	1000元
普通柿饼	16吨	5000元
特级霜降柿饼	8吨	8000元

由于生产条件的限制，两种加工方式不能同时进行，为此公司研制了两种可行方案：

方案1：尽可能多地生产为特级霜降柿饼，没来得及加工的新鲜柿子，在市场上直接销售；

方案2：先将部分新鲜柿子加工为特级霜降柿饼，再将剩余的新鲜柿子加工为普通柿饼，恰好15天完成．

请问：哪种方案获利更多？获利多少元？

查看试题解析

24.
【背景知识】
数轴是我们学习数学的一个重要工具，利用数轴可以很好地将数与形结合．
如图，若数轴上 $A ， B$ 两点表示的数分别为 $a ， b$ ，则 $A ， B$ 两点之间的距离 $A B = | b - a |$ ，例如， $a = - 2 ， b = 1$ ，则 $A B = | 1 - (- 2) | = 1 - (- 2) = 3$ ．

(1)、【问题情境】
如图， $A ， B$ 两点在数轴上对应的数分别为 $- 8$ 和12，甲、乙分别从 $A ， B$ 处同时出发，甲的速度为1个单位长度/秒，乙的速度为3个单位长度/秒，设运动的时间为秒．
$A B =$ ．

(2)、【综合运用】
如果甲、乙相向运动（甲向右运动，乙向左运动），记相遇点为 $P$ ，则点 $P$ 表示的数为，此时 $t =$ ．

(3)、如果甲、乙都向左运动，
①当为何值时，乙恰好追上甲？
②当为何值时，甲、乙之间恰好相距5个单位长度？

查看试题解析

	甲	乙
进价（元/件）	20	30
售价（元/件）	25	40