北师大版数学七年级上册期末冲刺满分攻略18 一元一次方程的认识及其解法

试卷更新日期：2024-01-03 类型：复习试卷

进入出卷网下载

一、选择题

1. 古代名著《算学启蒙》中有一题：良马日行二百三十里，驽马日行一百三十里．驽马先行一十一日，问良马几何追及之？意思是：跑得快的马每天走230里，跑得慢的马每天走130里．慢马先走11天，快马几天可追上慢马？若设快马x天可追上慢马，则可列方程为（）

A、 $230 (x - 11) = 130 x + 130 \times 11$ B、 $230 x = 130 x - 11 \times 130$ C、 $230 (x - 11) = 130 x + 130$ D、 $230 x = 130 x + 11 \times 130$

查看试题解析
2. 如图是长为a ，宽为b的小长方形卡片，把六张这样的小长方形卡片不重叠地放在一个底面为长方形（长为8，宽为6）的盒子底部（如图），盒子底部未被卡片覆盖的部分用阴影表示，则两块阴影部分的周长之和为（）

A、16 B、24 C、20 D、28

查看试题解析
3. 把mn=pq（mn≠0）写成比例式，写错的是（　　）

A、 $\frac{m}{p} = \frac{q}{n}$ B、 $\frac{p}{m} = \frac{n}{q}$ C、 $\frac{q}{m} = \frac{n}{p}$ D、 $\frac{m}{n} = \frac{p}{q}$

查看试题解析
4. 下列变形正确的是（）

A、若 $3 x - 1 = 2 x + 1$ ，则 $3 x + 2 x = 1 + 1$ B、若 $3 (x + 1) - 5 (1 - x) = 0$ ，则 $3 x + 3 - 5 - 5 x = 0$ C、若 $1 - \frac{3 x - 1}{2} = x$ ，则 $2 - 3 x - 1 = x$ D、若 $\frac{x + 1}{0.2} - \frac{x}{0.3} = 10$ ，则 $\frac{x + 1}{2} - \frac{x}{3} = 1$

查看试题解析
5. 小明在做解方程作业时，不小心将方程中的一个常数污染了看不清楚，被污染的方程是： $2 y - \frac{1}{2} = \frac{1}{2} y -$ ，怎么办呢？小明想了一想，便翻看书后答案，此方程的解是 $y = - \frac{5}{3}$ ，于是很快就补好了这个常数，你能补出这个常数吗？它应是（）

A、4 B、3 C、2 D、1

查看试题解析
6. 若关于x的一元一次方程 $\frac{3 x - 5 m}{2} - \frac{x - m}{3} = 19$ 的解，比关于x的一元一次方程﹣2（3x﹣4m）＝1﹣5（x﹣m）的解大15，则m＝（）

A、2 B、1 C、0 D、﹣1

查看试题解析
7. 代数式2ax+5b的值会随x的取值不同而不同，下表是当x取不同值时对应的代数式的值，则关于x的方程2ax+5b=4的解是（）

x

-4

-3

-2

-1

0

2ax+5b

12

8

4

0

-4

A、12 B、4 C、-2 D、0

查看试题解析
8. 方程3x+4＝2x﹣5移项后，正确的是（）

A、3x+2x＝4﹣5 B、3x﹣2x＝4﹣5 C、3x﹣2x＝﹣5﹣4 D、3x+2x＝﹣5﹣4

查看试题解析
9. 已知方程7x+2=3x-6与x-1=k 的解相同，则3k²-1的值为（）

A、18 B、20 C、26 D、-26

查看试题解析
10. 若方程3+▲=2x的解为x=5，则▲=（）

A、9 B、7 C、5 D、4

查看试题解析

二、填空题

11. 如图是一个数表，现用一个矩形在数表中任意框出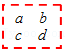4个数，当a+b+c+d＝32时，a＝．

查看试题解析
12. 如图所示是一个运算程序，若输出的结果是-2，则输入的值为．

查看试题解析
13. $A$ ， $B$ 两地相距 $450$ 千米，甲、乙两车分别从 $A$ ， $B$ 两地同时出发，相向而行，已知甲速度为 $120$ 千米/时，乙速度为 $80$ 千米/时， $t$ 小时后两车相距 $50$ 千米， $t$ 满足的方程是.

查看试题解析
14. 小邱认为，若 $a c = b c$ ，则 $a = b$ .你认为小邱的观点正确吗？ (填“是”或“否”)，并写出你的理由： .

查看试题解析
15. 图（①）的等臂天平呈平衡状态，其中左侧秤盘有一袋石头，右侧秤盘有一袋石头和2个各20克的砝码．将左侧袋中一颗石头移至右侧秤盘，并拿走右侧秤盘的1个砝码后，天平仍呈平衡状态，如图（②）所示．则被移动石头的重量是克．

查看试题解析
16. 已知关于x的方程ax+b=0，有以下四种说法：
①若x=1是该方程的解，则a+b=0；②若a=﹣1，则x=b是该方程的解；③若a≠0，则该方程的解是x=﹣ $\frac{b}{a}$ ；④若a=0，b≠0，则该方程无解．
其中所有正确说法的序号是．

查看试题解析

三、解答题

17. 解方程：

(1)、 $4 x = 3 x + 7$ ；

(2)、 $\frac{x + 1}{2} - \frac{2 x - 1}{3} = 1$ ．

查看试题解析
18. 用“☆”定义一种新运算：对于任意有理数a和b，规定a☆b=ab²+2ab+a．
如：1☆3=1×3²+2×1×3+1=16．
（1）求（﹣2）☆3的值；
（2）若（ $\frac{a + 1}{2}$ ☆3）☆（﹣ $\frac{1}{2}$ ）=8，求a的值；
（3）若2☆x=m，（ $\frac{1}{4}$ x）☆3=n（其中x为有理数），试比较m，n的大小．

查看试题解析
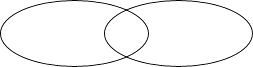
19. 在初中数学中，我们学习了各种各样的方程．以下给出了6个方程，请你把属于一元方程的序号填入圆圈（1）中，属于一次方程的序号填入圆圈（2）中，既属于一元方程又属于一次方程的序号填入两个圆圈的公共部分．
①3x+5=9：②x²+4x+4=0；③2x+3y=5：④x²+y=0；⑤x﹣y+z=8：⑥xy=﹣1．

查看试题解析
20. 某工人原计划13小时生产一批零件，后因每小时多生产10件，用12小时不但完成了任务，而且比原计划多生产了60件，问原计划生产多少零件？

查看试题解析
21. 1．植树节甲班植树的株数比乙班多20%，乙班植树的株树比甲班的一半多10株，若乙班植树x株．
（1）列两个不同的含x的代数式表示甲班植树的株数．
（2）根据题意列出以x为未知数的方程．
（3）检验乙班、甲班植树的株数是不是分别为25株和35株．

查看试题解析
22. 如图，已知点A在数轴上对应的数为a，点B对应的数为b，且a、b满足|a+3|+（b﹣2）²=0．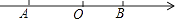

(1)、求A、B两点的坐标；

(2)、点C在数轴上对应的数为x，且x是方程2x+1= $\frac{1}{2}$ x﹣8的解
①求线段BC的长；
②在数轴上是否存在点P，使PA+PB=BC？求出点P对应的数；若不存在，说明理由．

查看试题解析
23. 某服装厂生产一种西装和领带，西装每套定价 $300$ 元，领带每条定价 $50$ 元．厂方在开展促销活动期间，向客户提供两种优惠方案：①买一套西装送一条领带；②西装和领带都按定价的 $90 %$ 付款．现某客户要到该服装厂购买西装 $20$ 套，领带 $x$ 条 $(x > 20)$ ：

(1)、若该客户按方案①购买，需付款元 $($ 用含 $x$ 的代数式表示 $)$ ；若该客户按方案②购买，需付款元 $($ 用含 $x$ 的代数式表示 $)$ ；

(2)、若 $x = 30$ ，通过计算说明此时按哪种方案购买较为合算？

(3)、当 $x = 30$ 时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．

查看试题解析
24. 对于有理数a、b定义一种新运算a⊗b＝ ${\begin{array}{l} 3 a - 2 b (a \geq b) \\ a - \frac{2}{3} b (a < b) \end{array}$ ，如5⊗3＝3×5﹣2×3＝9，1⊗3＝1﹣ $\frac{2}{3}$ ×3＝﹣1；请按照这个定义完成下列计算：

(1)、计算
①5⊗（﹣3）＝ ▲ ；
②（﹣5）⊗（﹣3）＝ ▲ ；
③若x⊗ $\frac{3}{2}$ ＝﹣3，求x`的值；

(2)、若A＝﹣2x³+ $\frac{2}{3} x^{2}$ ﹣x+1，B＝﹣2x³+x²﹣x+ $\frac{3}{2}$ ，且A⊗B＝﹣4，求3x³+ $\frac{3}{2}$ x+2的值；

(3)、若x和k均为正整数，且满足 $(\frac{k}{3} x + k) \otimes (\frac{1}{3} x + 1) = \frac{4}{3}$ x+12，求k的值．

查看试题解析

x	-4	-3	-2	-1	0
2ax+5b	12	8	4	0	-4