北师大版数学七年级上册期末冲刺满分攻略17 多边形和圆的初步认识
试卷更新日期:2024-01-03 类型:复习试卷
一、选择题
-
1. 如果一个多边形从一个顶点出发最多能画三条对角线,则这个多边形的边数为( ) .A、4 B、5 C、6 D、72. 过一个多边形的顶点可作5条对角线,则这个多边形是( )A、六边形 B、七边形 C、八边形 D、九边形3. 如图所示,设M表示平行四边形,N表示矩形,P表示菱形,Q表示正方形,则下列四个图形中,能表示它们之间关系的是( )A、
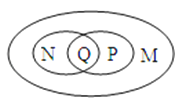 B、
B、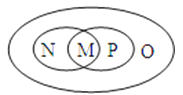 C、
C、 D、
D、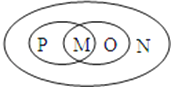 4. 下列说法中,正确是( )A、对角线相等的四边形是矩形 B、一组对边平行,另一组对边相等的四边形是平行四边形 C、对角线互相垂直平分的四边形是菱形 D、一组邻边相等,并且有一个内角为直角的四边形是正方形5. 下列说法中,正确的是( )A、两个半圆是等弧 B、同圆中优弧与半圆的差必是劣弧 C、长度相等的弧是等弧 D、同圆中优弧与劣弧的差必是优弧6.
4. 下列说法中,正确是( )A、对角线相等的四边形是矩形 B、一组对边平行,另一组对边相等的四边形是平行四边形 C、对角线互相垂直平分的四边形是菱形 D、一组邻边相等,并且有一个内角为直角的四边形是正方形5. 下列说法中,正确的是( )A、两个半圆是等弧 B、同圆中优弧与半圆的差必是劣弧 C、长度相等的弧是等弧 D、同圆中优弧与劣弧的差必是优弧6.点A、O、D与点B、O、C分别在同一直线上,图中弦的条数为( )
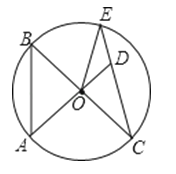 A、2 B、3 C、4 D、57. 图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )
A、2 B、3 C、4 D、57. 图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )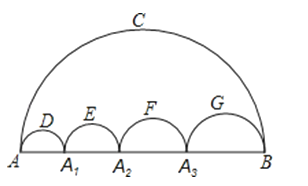 A、甲先到B点 B、乙先到B点 C、甲、乙同时到B D、无法确定8. n边形所有对角线的条数有( )A、 条 B、 条 C、 条 D、 条9. 如果一个四边形的两条对角线互相垂直平分且相等,那么这个四边形是( )A、矩形 B、菱形 C、正方形 D、都有可能10. 从六边形的一个顶点出发,可以画出m条对角线,它们将六边形分成n个三角形.则m、n的值分别为( )A、4,3 B、3,3 C、3,4 D、4,4
A、甲先到B点 B、乙先到B点 C、甲、乙同时到B D、无法确定8. n边形所有对角线的条数有( )A、 条 B、 条 C、 条 D、 条9. 如果一个四边形的两条对角线互相垂直平分且相等,那么这个四边形是( )A、矩形 B、菱形 C、正方形 D、都有可能10. 从六边形的一个顶点出发,可以画出m条对角线,它们将六边形分成n个三角形.则m、n的值分别为( )A、4,3 B、3,3 C、3,4 D、4,4二、填空题
-
11. 一个多边形从一个顶点出发,最多可以作2条对角线,则这个多边形的边数是 .12. 我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称 .13.
能伸缩的校门,它利用了四边形的一个性质是 .
 14.
14.从知识结构来看,平行四边形、矩形、菱形、正方形的包含关系可以如图表示,则其中最大的椭圆表示的是 形,阴影部分表示的是 形.
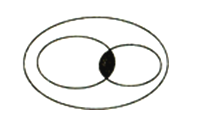 15. 如果一个四边形的两条对角线相等,那么称这个四边形为“等对角线四边形”.写出一个你所学过的特殊的等对角线四边形的名称 .16.
15. 如果一个四边形的两条对角线相等,那么称这个四边形为“等对角线四边形”.写出一个你所学过的特殊的等对角线四边形的名称 .16.如图:AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于E点,已知AB=2DE,∠E=16°,则∠AOC的大小是 °.

三、解答题
-
17. 过m边形的一个顶点有8条对角线,n边形没有对角线,p边形有p条对角线,试求(m﹣p)n的值.18. 为了说明各种三角形之间的关系,小明画了如下结构图:

请你采用类似的方式说明下述几个概念之间的关系:正方形、四边形、梯形、菱形、平行四边形、矩形.
19. 阅读下列内容,并答题:我们知道计算n边形的对角线条数公式为 , 如果有一个n边形的对角线一共有20条,则可以得到方程=20,去分母得n(n﹣3)=40;∵n为大于等于3的整数,且n比n﹣3的值大3,∴满足积为40且相差3的因数只有8和5,符合方程n(n﹣3)=40的整数n=8,即多边形是八边形.根据以上内容,问:
(1)若有一个多边形的对角线一共有14条,求这个多边形的边数;
(2)A同学说:“我求得一个多边形的对角线一共有30条.”你认为A同学说地正确吗?为什么?
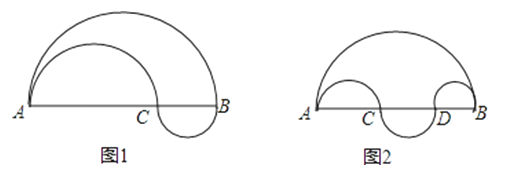
20. (1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近;(2)如果甲、乙走的路程图改成图2,两人走的路程远近相同吗?
 21.
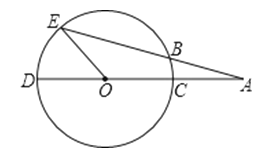
21.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.
(1)求∠AOB的度数.
(2)求∠EOD的度数.
 22. 将一个半径为4cm的圆分割成三个扇形.(1)、它们的圆心角的比为2∶3∶5,求这三个扇形圆心角的度数;(2)、若分成4个大小相同的扇形,则每个扇形的圆心角为多少度?(3)、若其中一个扇形的圆心角为30o , 你会计算这个扇形的面积吗?23.(1)、从一个五边形的同一顶点出发,分别连接这个顶点与其余各顶点,可以把这个五边形分成个三角形.若是一个六边形,可以分割成个三角形.n边形可以分割成个三角形.
22. 将一个半径为4cm的圆分割成三个扇形.(1)、它们的圆心角的比为2∶3∶5,求这三个扇形圆心角的度数;(2)、若分成4个大小相同的扇形,则每个扇形的圆心角为多少度?(3)、若其中一个扇形的圆心角为30o , 你会计算这个扇形的面积吗?23.(1)、从一个五边形的同一顶点出发,分别连接这个顶点与其余各顶点,可以把这个五边形分成个三角形.若是一个六边形,可以分割成个三角形.n边形可以分割成个三角形. (2)、若将n边形内部任意取一点P,将P与各顶点连接起来,则可将多边形分割成多少个三角形?(3)、若点P取在多边形的一条边上(不是顶点),再将P与n边形各顶点连接起来,则可将多边形分割成多少个三角形?24. 有三条长度均为a的线段,分别按以下要求画圆.
(2)、若将n边形内部任意取一点P,将P与各顶点连接起来,则可将多边形分割成多少个三角形?(3)、若点P取在多边形的一条边上(不是顶点),再将P与n边形各顶点连接起来,则可将多边形分割成多少个三角形?24. 有三条长度均为a的线段,分别按以下要求画圆.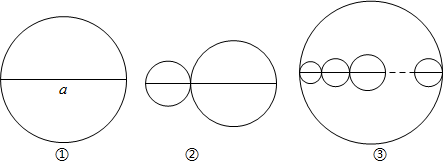 (1)、如图①,以该线段为直径画一个圆,记该圆的周长为C1;如图②,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为C2 , 请指出C1和C2的数量关系,并说明理由;(2)、如图③,当a=11时,以该线段为直径画一个大圆,再在大圆内画若干小圆,这些小圆的直径都和大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有小圆的周长的和为.(直接填写答案,结果保留π)
(1)、如图①,以该线段为直径画一个圆,记该圆的周长为C1;如图②,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为C2 , 请指出C1和C2的数量关系,并说明理由;(2)、如图③,当a=11时,以该线段为直径画一个大圆,再在大圆内画若干小圆,这些小圆的直径都和大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有小圆的周长的和为.(直接填写答案,结果保留π)