北京市房山区2023-2024学年九年级上学期期中数学试卷

试卷更新日期：2024-01-03 类型：期中考试

进入出卷网下载

一、选择题（本大题共8小题，共24分。在每小题列出的选项中，选出符合题目的一项）

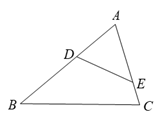
1. 已知 $2 x = 3 y (x y \neq 0)$ ，那么下列比例式中成立的是（）

A、 $\frac{x}{y} = \frac{2}{3}$ B、 $\frac{x}{3} = \frac{y}{2}$ C、 $\frac{x}{2} = \frac{y}{3}$ D、 $\frac{x}{2} = \frac{3}{y}$

查看试题解析
2. 抛物线 $y = x^{2} + 1$ 的顶点坐标是（）

A、 $(- 1，0)$ B、 $(0 ， - 1)$ C、 $(0，1)$ D、 $(1，0)$

查看试题解析
3. 我国著名数学家华罗庚曾为普及优选法作出重要贡献，优选法中有一种0.618法应用了（）

A、黄金分割数 B、平均数 C、众数 D、中位数

查看试题解析
4. 如图，在 $∆ A B C$ 中， $D E / / B C$ ， $A D = 3$ ， $D B = 6$ ， $A E = 2$ ，则 $E C$ 的长为（）

A、 $2$ B、 $4$ C、 $6$ D、 $9$

查看试题解析
5. 把二次函数 $y = 3 x^{2}$ 的图象向右平移 $2$ 个单位，再向下平移 $1$ 个单位，所得到的图象对应的二次函数表达式是（）

A、 $y = 3 (x + 2)^{2} + 1$ B、 $y = 3 (x + 2)^{2} - 1$ C、 $y = 3 (x - 2)^{2} - 1$ D、 $y = 3 (x - 2)^{2} + 1$

查看试题解析
6. 已知蓄电池两端电压 $U$ 为定值，电流 $I$ 与 $R$ 的函数关系为 $I = \frac{U}{R} .$ 当 $I = 3 A$ 时， $R = 8 Ω$ ，则当 $I = 6 A$ 时， $R$ 的值为（）

A、 $4 Ω$ B、 $6 Ω$ C、 $8 Ω$ D、 $10 Ω$

查看试题解析
7. 若点 $A (- 1 ， y_{1})$ ， $B (2 ， y_{2})$ ， $C (4 ， y_{3})$ 在抛物线 $y = x^{2} - 4 x + 5$ 上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系为（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{2} < y_{3} < y_{1}$

查看试题解析
8. 已知：在四边形 $A B C D$ 中， $A B / / C D$ ， $∠ B = 90^{\circ}$ ，点 $E$ 是线段 $B C$ 上一点，且 $A E$ 平分 $∠ B A D$ ， $D E$ 平分 $∠ A D C$ ，给出下面四个结论：
$① A E ⊥ D E$ ； $② ∠ A E B = ∠ E D C$ ； $③ A B \cdot C D = B E \cdot E C$ ； $④ B E \cdot E D = A E \cdot E C$
上述结论中，所有正确结论的序号是（）

A、 $① ②$ B、 $③ ④$ C、 $① ② ③$ D、 $① ② ③ ④$

查看试题解析

二、填空题（本大题共8小题，共24分）

9. 在函数 $y = \frac{1}{x - 5}$ 中，自变量 $x$ 的取值范围是．

查看试题解析
10. 已知 $\frac{y}{x} = \frac{1}{2}$ ，则 $\frac{x + y}{x} =$ ．

查看试题解析
11. 请写出一个图象的顶点为 $(0，0)$ 的二次函数的表达式：．

查看试题解析
12. 若两个相似三角形的相似比是1：2，则它们的周长比是．

查看试题解析
13. 如图，点 $D$ ， $E$ 分别在△ $A B C$ 的 $A B$ ， $A C$ 边上．只需添加一个条件即可证明△ $A D E$ ∽△ $A C B$ ，这个条件可以是．（写出一个即可）

查看试题解析
14. 如图，已知反比例函数 $y = \frac{k}{x}$ 的图象经过点 $A$ ，且 $A B ⊥ O B$ ． $△ A O B$ 的面积为 $2$ ，则 $k$ 的值为。

查看试题解析
15. 如图，某中学综合与实践小组要围成一个矩形菜园 $A B C D$ ，其中一边 $A D$ 靠墙，其余的三边 $A B$ ， $B C$ ， $C D$ 用总长为 $40$ 米的栅栏围成．设矩形 $A B C D$ 的边 $A B = x$ 米，面积为 $S$ 平方米．

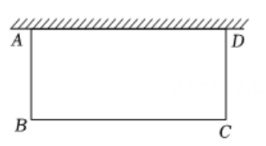(1)、活动区面积 $S$ 与 $x$ 之间的关系式为；

(2)、菜园 $A B C D$ 最大面积是平方米．

查看试题解析
16. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象经过 $A (0，3)$ ， $B (2 ， - 1)$ ， $C (4，3)$ 三点．
下面四个结论：
$①$ 抛物线开口向下；
$②$ 当 $x = 2$ 时， $y$ 取最小值 $- 1$ ；
$③$ 当 $m \leq - 1$ 时，一元二次方程 $a x^{2} + b x + c = m$ 必有两个不相等实根；
$④$ 直线 $y = k x + c (k \neq 0)$ 经过点 $A$ ， $B$ ，当 $k x + c > a x^{2} + b x + c$ 时， $x$ 的取值范围是 $0 < x < 2$ ．
所有正确结论的序号是．

查看试题解析

三、解答题（本大题共12小题，共96分。解答应写出文字说明，证明过程或演算步骤）

17. 如图， $A C$ ， $B D$ 相交于点 $O$ ， $∠ A = ∠ D$ ．
求证： $∆ A O B ~ ∆ D O C$ ．

查看试题解析
18. 若 $x ： 2 = 3 ： (x + 5)$ ，求 $x$ 的值．

查看试题解析
19. 已知二次函数 $y = x^{2} + 2 x - 3$ ．

(1)、求出二次函数图象的对称轴和与 $y$ 轴的交点坐标；

(2)、在平面直角坐标系中画出图象，请结合图象直接写出 $y < 0$ 时， $x$ 的取值范围．

查看试题解析
20. 如图，在 $4 \times 4$ 的正方形网格中，每个小正方形的顶点称为格点． $∆ A B C$ 和 $∆ D E F$ 的顶点都在边长为 $1$ 的小正方形的格点上．

(1)、则 $∠ D E F =$ $°$ ， $A C =$ ；

(2)、判断 $∆ A B C$ 与 $∆ D E F$ 是否相似．若相似，请说明理由．

查看试题解析
21. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象上部分点的横坐标 $x$ ，纵坐标 $y$ 的对应值如下表：

$x$

$\dots$

$- 2$

$- 1$

$0$

$1$

$2$

$3$

$4$

$\dots$

$y$

$\dots$

$5$

$0$

$- 3$

$- 4$

$- 3$

$0$

$n$

$\dots$
求这个二次函数的表达式及 $n$ 的值．

查看试题解析

22. 同学们在探究学习中发现：“三角形内角的角平分线分对边所得的两条线段与这个角的两边对应成比例”

.

下面是小明同学思考出的两种不同的证明方法，请选择其中一种完成证明．

已知：如图， $∆ A B C$ 中， $A D$ 是角平分线．求证： $\frac{A B}{A C} = \frac{B D}{D C}$ ．
方法一证明：如图，过点 $C$ 作 $C E / / A D$ ，与 $B A$ 的延长线交于点 $E$ ．	方法二证明：如图，过点 $D$ 作 $D M ⊥ A B$ 于 $M$ ，过点 $D$ 作 $D N ⊥ A C$ 于 $N$ ．

查看试题解析

23. 在平面直角坐标系 $x O y$ 中，一次函数 $y = x + 2$ 的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象相交于点 $A (1 ， m)$ ．

(1)、求这个反比例函数的表达式；

(2)、请结合图象直接写出 $\frac{k}{x} > x + 2$ 时， $x$ 的取值范围是．

查看试题解析
24. 小宇在学习过程中遇到了一个函数 $y = |x| + \frac{1}{x} (x \neq 0)$ ．
下面是小宇对其探究的过程，请补充完整：

(1)、对于函数 $y_{1} = \frac{1}{x}$ ，当 $x < 0$ 时， $y_{1}$ 随 $x$ 的增大而减小，
对于函数 $y_{2} = |x|$ ，当 $x < 0$ 时， $y_{2}$ 随 $x$ 的增大
而结合上述分析，进一步探究发现，对于函数 $y$ ，当 $x < 0$ 时， $y$ 随 $x$ 的增大而；

(2)、当 $x > 0$ 时，对于函数 $y$ 与 $x$ 的几组对应值如下表：

$x$

$\dots$

$\frac{1}{4}$

$\frac{1}{2}$

$1$

$\frac{3}{2}$

$2$

$\frac{5}{2}$

$\dots$

$y$

$\dots$

$\frac{17}{4}$

$\frac{5}{2}$

$2$

$\frac{13}{6}$

$\frac{5}{2}$

$\frac{29}{10}$

$\dots$
在平面直角坐标系 $x O y$ 中，画出当 $x > 0$ 时函数 $y$ 的图象．

(3)、过点 $(0 ， m)$ 作平行于 $x$ 轴的直线 $l$ ，结合 $(1) (2)$ 的分析，解决问题：
若直线 $l$ 与函数 $y = |x| + \frac{1}{x} (x \neq 0)$ 的图象有两个交点，则 $m =$ ．

查看试题解析
25. 如图，在平行四边形 $A B C D$ 中，延长 $A D$ 至点 $E$ ，使 $D E = \frac{1}{2} A D$ ，连接 $B E$ 交 $C D$ 于点 $F$ ．

(1)、求证： $∆ A B E ∽ ∆ C F B$ ；

(2)、若 $C F = 2$ ，求 $A B$ 的长．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} - (a + 1) x (a \neq 0)$ ，若 $M (x_{1} ， y_{1})$ ， $N (x_{2} ， y_{2})$ 为抛物线上两个不同的点，设抛物线的对称轴为 $x = t$ ．

(1)、当 $t = 1$ 时，求 $a$ 的值；

(2)、若对于 $x_{1} > x_{2} \geq - \frac{1}{2}$ ，都有 $y_{1} < y_{2}$ ，求 $a$ 的取值范围．

查看试题解析
27. 如图，在 $∆ A B C$ 中， $A B = A C$ ， $∠ B A C = 90^{\circ}$ ，过点 $A$ 的射线与斜边 $B C$ 交于点 $D$ ， $C E ⊥ A D$ 于点 $E$ ．

(1)、求证： $∠ B A D = ∠ A C E$ ；

(2)、连接 $B E$ ，若满足 $D C = 2 B D$ ， $A E = 1$ ，求 $B E$ 的值．

查看试题解析
28. 定义：在平面直角坐标系 $x O y$ 中，当点 $N$ 在图形 $M$ 的内部，或在图形 $M$ 上，且点 $N$ 的横坐标和纵坐标相等时，则称点 $N$ 为图形 $M$ 的“和谐点”．

(1)、如图，矩形 $A B C D$ 的顶点坐标分别是 $A (- 1，2)$ ， $B (- 1 ， - 1)$ ， $C (3 ， - 1)$ ， $D (3，2)$ ，在点 $M_{1} (1，1)$ ， $M_{2} (2，2)$ ， $M_{3} (3，3)$ 中，是矩形 $A B C D$ “和谐点”的是；

(2)、点 $G (2，2)$ 是反比例函数 $y_{1} = \frac{k}{x}$ 图象上的一个“和谐点”，则该函数图象上的另一个“和谐点” $H$ 的坐标是，直线 $G H$ 的表达式是 $y_{2} =$ ；

(3)、已知点 $A$ ， $B$ 是抛物线 $y = - \frac{1}{2} {(x - 1)}^{2} + 5$ 上的“和谐点”，点 $A$ 在点 $B$ 的左侧，点 $C$ 是抛物线的顶点，连接 $A C$ ， $A B$ ， $B C$ ，求点 $A$ ， $B$ 的坐标，并直接写出 $∆ A B C$ 的面积．

查看试题解析

$x$	$\dots$	$- 2$	$- 1$	$0$	$1$	$2$	$3$	$4$	$\dots$
$y$	$\dots$	$5$	$0$	$- 3$	$- 4$	$- 3$	$0$	$n$	$\dots$

$x$	$\dots$	$\frac{1}{4}$	$\frac{1}{2}$	$1$	$\frac{3}{2}$	$2$	$\frac{5}{2}$	$\dots$
$y$	$\dots$	$\frac{17}{4}$	$\frac{5}{2}$	$2$	$\frac{13}{6}$	$\frac{5}{2}$	$\frac{29}{10}$	$\dots$