四川省泸州市2023-2024学年九年级上学期第一次月考数学试卷

试卷更新日期：2024-01-03 类型：月考试卷

进入出卷网下载

一、单选题

1. -2023的相反数是（）

A、 $- \frac{1}{2023}$ B、-2023 C、 $\frac{1}{2023}$ D、2023

查看试题解析
2. 从水利部长江水利委员会获悉，截止2023年3月30日17时，南水北调中线一期工程自2014年12月全面通水以来，已累计向受水区实施生态补水约90亿立方米．其中9000000000用科学记数法表示为（）

A、 $9 \times 1 0^{8}$ B、 $9 \times 1 0^{9}$ C、 $9 \times 1 0^{10}$ D、 $9 \times 1 0^{11}$

查看试题解析
3. 下列运算正确的是（）

A、 $m^{3} - m^{2} = m$ B、 $3 m^{2} \cdot 2 m^{3} = 6 m^{5}$ C、 $3 m^{2} + 2 m^{3} = 5 m^{5}$ D、 ${(2 m^{2})}^{3} = 8 m^{5}$

查看试题解析
4. 如图，直线 l₁∥l₂ ， ∠1＝40°，∠2＝75°，则∠3 等于（）

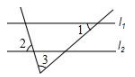A、55° B、60° C、65° D、70°

查看试题解析
5. 一元二次方程 $x^{2} - 2 (3 x - 2) + (x + 1) = 0$ 的一般形式是（）

A、 $x^{2} - 5 x + 5 = 0$ B、 $x^{2} + 5 x - 5 = 0$ C、 $x^{2} + 5 x + 5 = 0$ D、 $x^{2} + 5 = 0$

查看试题解析
6. 抛物线 $y = x^{2} + 4$ 与 $y$ 轴的交点坐标是（）

A、 $(4 ， 0)$ B、 $(- 4 ， 0)$ C、 $(0 ， - 4)$ D、 $(0 ， 4)$

查看试题解析
7. 某市2020年人均可支收入为2.36万元，2022年达到2.7万元，若2020年至2022年间每年人均可支配收入的增长率都为x，则下面所列方程正确的是（）

A、 $2.7 (1 + x)^{2} = 2.36$ B、 $2.36 (1 + x)^{2} = 2.7$ C、 $2.7 (1 - x)^{2} = 2.36$ D、 $2.36 (1 - x)^{2} = 2.7$

查看试题解析
8. 已知扰物线 $y = a x^{2} (a > 0)$ 过 $A (- 2 ， y_{1}) ， B (1 ， y_{2})$ 两点，则下列关系式一定正确的是（）

A、 $y_{1} > 0 > y_{2}$ B、 $y_{2} > 0 > y_{1}$ C、 $y_{1} > y_{2} > 0$ D、 $y_{2} > y_{1} > 0$

查看试题解析
9. 已知 m， n 是一元二次方程 $x^{2} + 2 x - 5 = 0$ 的两个根，则 $m^{2} + m n + 2 m$ 的值为（）

A、3 B、-10 C、0 D、10

查看试题解析
10. 如果关于x的方程 $\frac{2 x + m}{x - 1} = 1$ 的解是正数，那么m的取值范围是（　　）

A、 $m > - 1$ B、 $m > - 1$ 且 $m \neq 0$ C、 $m < - 1$ D、 $m < - 1$ 且 $m \neq - 2$

查看试题解析
11. 如图，正方形OABC有三个顶点在抛物线 $y = \frac{1}{4} x^{2}$ 上，点 $O$ 是原点，顶点 $B$ 在 $y$ 轴上则顶点 $A$ 的坐标是（）

A、 $(2 ， 2)$ B、 $(\sqrt{2} ， \sqrt{2})$ C、 $(4 ， 4)$ D、 $(2 \sqrt{2} ， 2 \sqrt{2})$

查看试题解析
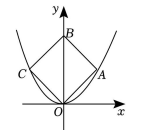12. 关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 给出下列说法：①若 $a + c = 0$ ，则方程必有两个实数根； ②若a+b+c=0，则方程必有两个实数根：③若 $b = 2 a + 3 c$ ，则方程有两个不等的实数根； ④若 $b^{2} - 5 a c < 0$ ，则方程一定没有实数根，其中说法正确的序号是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

二、填空题

13. 因式分解： $a - a b^{2} =$ .

查看试题解析
14. 如图，直线 $y_{1} = - 2 x - 3$ 与直线 $y_{2} = k x + 4$ 交于点 $A (a ， 1)$ ，则关于x的不等式 $- 2 x - 3 > k x + 4$ 的解集是．

查看试题解析
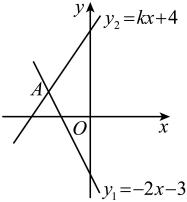15. 已知 m， n 是方程 $x^{2} - x - 2 = 0$ 的两个根，则代数式 $2 m^{2} - 3 m - n$ 的值等于

查看试题解析
16. 如图，在矩形ABCD中，AB=6，BC=8，点E、F分别是边AB、BC上的动点，且EF=4，点G是EF的中点，AG、CG，则四边形AGCD面积的最小值为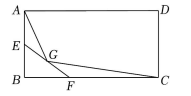

查看试题解析

三、解答题

17. 计算： $(- 1)^{2023} - | - 6 | + {(- \frac{1}{2})}^{- 2} - (3.14 - π)^{0} + \sqrt[3]{64}$ .

查看试题解析
18. 已知：如图，AB∥DE，AB=DE，AF=DC．求证：∠B=∠E．

查看试题解析
19. 解方程：

(1)、 $x^{2} - 2 x - 3 = 0$ ；

(2)、 $(x + 1)^{2} = (3 - 2 x)^{2}$ .

查看试题解析
20. 某校学生会向全校1900名学生发起了爱心捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图1和图2，请根据相关信息，解答系列问题：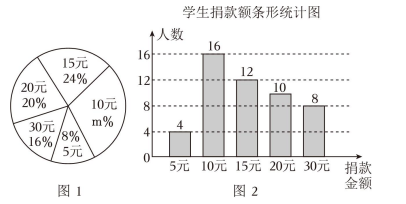

(1)、本次接受随机抽样调查的学生人数为人，图 1 中 m 的值是．

(2)、求本次调查获取的样本数据的平均数、众数和中位数；

(3)、根据样本数据，估计该校本次活动捐款金额为 10 元的学生人数．

查看试题解析
21. 某花农培育甲种樱花3株，乙种樱花2株，共需要成本1700元；培育甲种樱花1株，乙种樱花2株，共需成本1500元．

(1)、求甲、乙两种樱花每株成本分别为多少元？

(2)、据市场调研，1株甲种樱花售价为160元，1株乙种樱花售价为840元．该花农决定在成本不超过29000元的前提下培育甲、乙两种樱花，若培育乙种樱花的株数是甲种樱花的3倍还多10株，那么要使总利润不少于5000元，花农有哪几种具体的培育方案？

(3)、求出选何种方案成本最少？

查看试题解析
22. 如图，眉山水街游人如织，交通十分拥挤．为了缓解这种交通状况，政府决定对水街的部分路段进行拓宽改造．在水街拓宽工程中，要伐掉一棵树AB，在地面上事先划定以B为圆心，半径与AB等长的圆形危险区，现在某工人站在离B点3米远的D处，从C点测得树的顶端A点的仰角为60°，树的底部B点的俯角为30°．

(1)、求大树的高度．（保留根号）

(2)、距离大树 $B$ 点 8 米远有一配电箱，配电箱是否处在危险区内？ $(\sqrt{3} \approx 1.7 ， \sqrt{2} \approx 1.4 ）$ 0

查看试题解析
23. 因粤港澳大湾区和中国特色社会主义先行示范区的双重利好，深圳已成为国内外游客最喜欢的旅游目的地城市之一，深圳著名旅游“网红打卡地”东部华侨城景区在2020年春节长假期间，共接待游客达20万人次，预计在2022年春节长假期间将接待游客达28.8万人次．

(1)、求东部华侨城景区 2020 至 2022 年春节长假期间接待游客人次的平均增长率；

(2)、东部华侨城景区一奶茶店销售一款奶茶，每杯成本价为6元，根据销售经验，在旅游旺季，若每杯定价25元，则平均每天可销售300杯，若每杯价格降低1元，则平均每天可多销售30杯，2022年春节期间，店家决定进行降价促销活动，则当每杯售价定为多少元时，既能让顾客获得最大优惠，又可让店家在此款奶茶实现平均每天6300元的利润额？

查看试题解析
24. 已知关于 $x$ 的一元二次方程： $k^{2} x^{2} + (1 - 2 k) x + 1 = 0$ 有两个不相等的实数根.

(1)、求 $k$ 的取值范围；

(2)、若原方程的两个实数根为 $x_{1} ， x_{2}$ ，且满足 $| x_{1} | + | x_{2} | = 2 x_{1} x_{2} - 3$ ，求 $k$ 的值.

查看试题解析
25. 如图，在平面直角坐标系中，一次函数l₁：y=x+b与l₂：y=kx+3分别经过x轴上的点B（1，0）．点C（4，0），交于点P，点D为直线l₂上一点．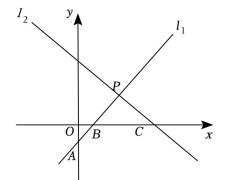

(1)、求点 P 的坐标；

(2)、若点D的横坐标小于点P的横坐标，连接OD，OP，当△BCP和△ODP的面积相等时，求点D的坐标；

(3)、在 l₁上是否存在点 E，使得以O，D，P，E为顶点的四边形是以OP为边的平行四边形？若存在，求出点E的坐标；如果不存在，请说明理由．

查看试题解析